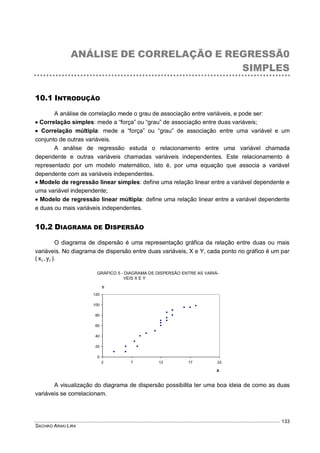
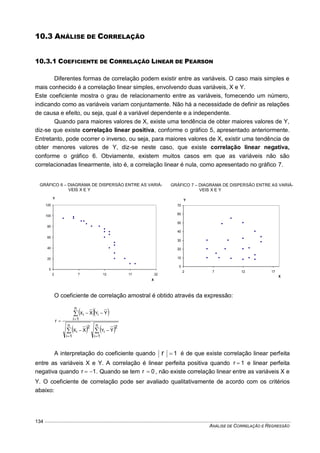
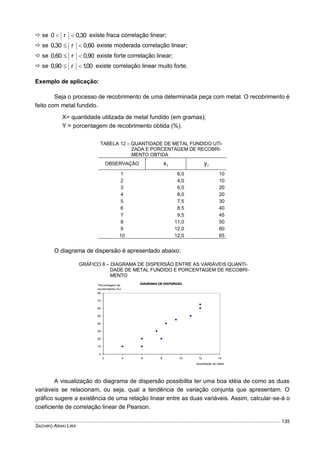
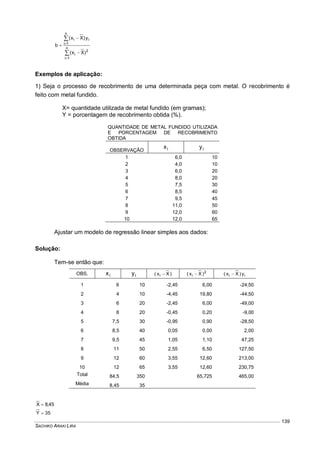
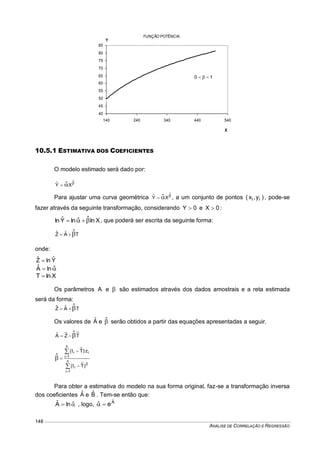
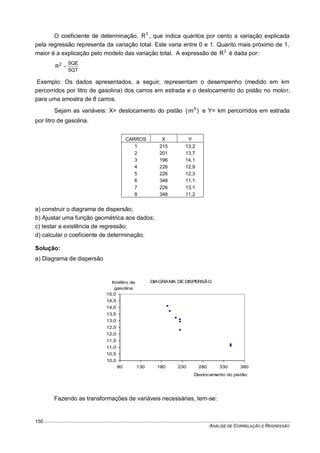
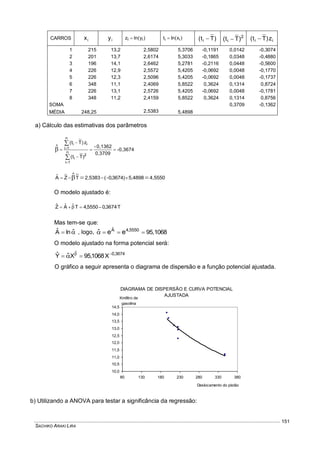
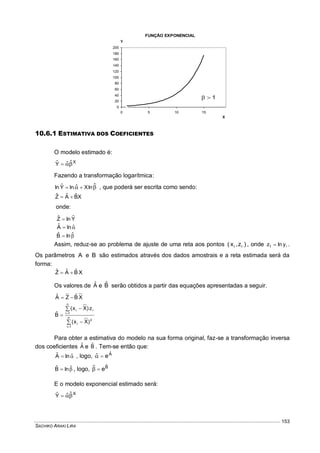
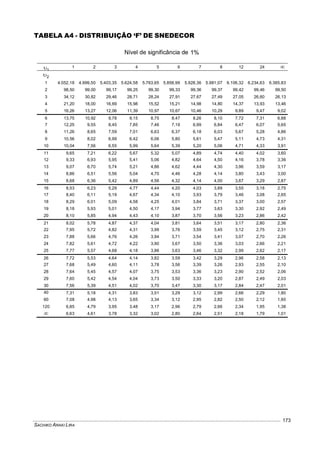
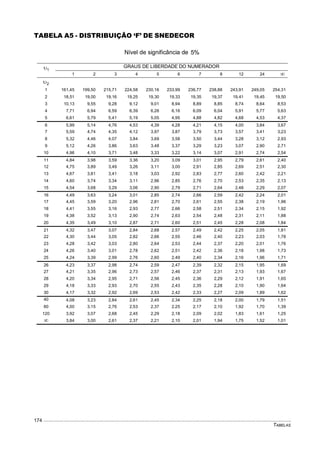
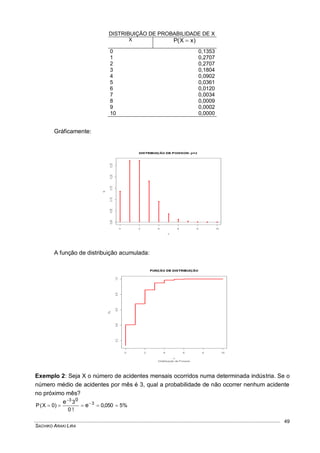
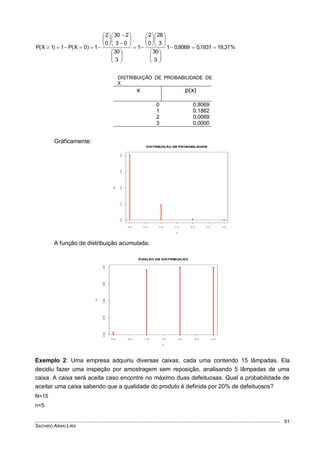
Este documento fornece um resumo conciso sobre estatística descritiva e probabilidades. Ele introduz conceitos como variável aleatória, tabelas, gráficos, medidas de tendência central e dispersão, experimentos aleatórios, eventos, definições de probabilidade, distribuições de probabilidades discretas e contínuas. O documento também inclui listas de exercícios relacionados a esses tópicos.

















































![VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES CONTÍNUAS DE PROBABILIDADES
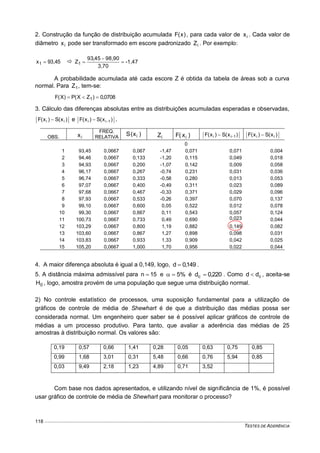
54
VARIÁVEIS ALEATÓRIAS E DISTRIBUIÇÕES
CONTÍNUAS DE PROBABILIDADES
4.1 DEFINIÇÕES
Definição 1: Seja X uma variável aleatória continua. A função densidade de probabilidade
)x(f , é uma função que satisfaz as seguintes condições:
0)x(f para todo XRx
1)x(d)x(f
.
Exemplo: Seja X uma variável contínua com função densidade de probabilidade dada por:
16
x
)x(f , 6x2
0)x(f , para qualquer outros valores.
A função densidade de probabilidade é:
Para 2x
8
1
16
2
)2(f
Para 4x
8
2
16
4
)4(f
Para 6x
8
3
16
6
)6(f
A condição 1)x(d)x(f
, indica que a área total limitada pela curva que representa )x(f e
o eixo das abcissas é igual a 1.
Seja o intervalo [a,b] de XR . A probabilidade de um valor de X pertencer a esse intervalo
será dada por:
b
a
dx)x(f)bXa(P , que representa a área sob a curva da função densidade
de probabilidade.
Para variáveis aleatórias contínuas, as probabilidades são interpretadas como áreas.
Sendo X uma variável aleatória continua, a probabilidade em um ponto é nula, então:
)bXa(P)bXa(P)bXa(P)bXa(P
Definição 2: Seja X uma variável aleatória. A função de distribuição acumulada ou de
repartição de X é definida como
)xX(P)x(F ](https://image.slidesharecdn.com/apostiladeestatstica2-170301155558/85/Apostila-de-estatistica-2-58-320.jpg)