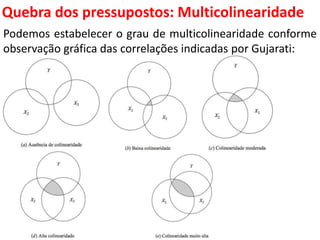
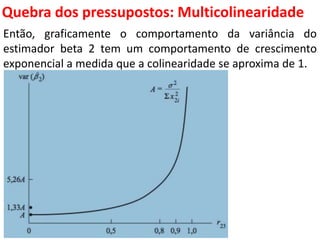
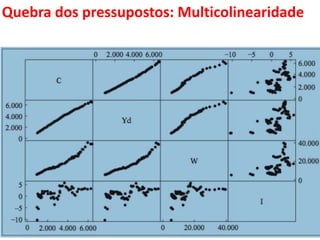
O documento aborda a multicolinearidade na análise de regressão múltipla, discutindo suas causas, efeitos e consequências práticas, além de métodos para sua identificação e correção. Destaca que a multicolinearidade pode levar a uma estimação imprecisa dos coeficientes de regressão, dificultando a interpretação dos resultados. O texto também menciona medidas corretivas e a importância de entender a natureza da multicolinearidade para melhorar a qualidade dos modelos econômicos.

1. Econometria
Tópico 3 – Regressão Múltipla
Quebra dos pressupostos: Multicolinearidade
Ricardo Bruno N. dos Santos
Professor Adjunto da Faculdade de Economia
e do PPGE (Economia) UFPA

2. Lembre-se que os vídeos necessários para o
acompanhamento dessa apresentação são todos os
vídeos que iniciam por 05, e encontram-se dentro da
pasta Vídeos no mediafire.
Link do mediafire:
http://www.mediafire.com/?q1dbpxh1b4uxo
No Slideshare:

3. Quebra dos pressupostos:
Multicolinearidade
A hipótese 8 do MCRL enfatiza que não há
multicolinearidade entre as variáveis independentes
presentes no modelo de regressão. Aqui estaremos
interessados em verificar:
1) Qual a natureza da multicolinearidade?
2) A multicolinearidade é realmente um problema?
3) Quais são suas consequências práticas?
4) Como é detectada?
5) Que medidas podem ser tomadas para atenuar o
problema da multicolinearidade?

4. Quebra dos pressupostos:
Multicolinearidade
Com relação a sua natureza a multicolinearidade surgiu
inicialmente com o conceito da existência de uma linearidade
“perfeita” ou exata entre duas variáveis independentes.
A principal causa da multicolinearidade é influenciar nos erros
padrão dos coeficientes, fazendo com que tais sejam
menores. Portanto, seu principal impacto é dificultar a
estimação dos parâmetros da equação.
Vejamos agora um exemplo concreto de multicolinearidade
perfeita e uma outra não perfeita, porém, alta.

5. Quebra dos pressupostos:
Multicolinearidade
Podemos estabelecer o grau de multicolinearidade conforme
observação gráfica das correlações indicadas por Gujarati:

6. Quebra dos pressupostos:
Multicolinearidade
Podemos observar o seguinte impacto da multicolinearidade
perfeita sobre os coeficientes e erros padrões de X:
𝛽2 =
𝑦𝑖 𝑥2𝑖 𝑥3𝑖
2
− 𝑦𝑖 𝑥3𝑖 𝑥2𝑖 𝑥3𝑖
𝑥2𝑖
2
𝑥3𝑖
2
− 𝑥2𝑖 𝑥3𝑖
2
e
𝑣𝑎𝑟 𝛽2 =
𝜎2
𝑥2𝑖
2
1 − 𝑟23
2

7. Quebra dos pressupostos:
Multicolinearidade
Ou seja, se a multicolinearidade for perfeita os coeficientes de
regressão das variáveis X serão indeterminados e seus erros
padrão infinitos. Se a multicolinearidade for menos que
perfeita, os coeficientes de regressão, embora sejam
determinados, possuirão grande erro padrão, o que impede a
precisão ou exatidão dos coeficientes.

8. Quebra dos pressupostos:
Multicolinearidade
Fontes da multicolinearidade:
1) Método da coleta de dados empregado.
2) Restrições ao modelo ou à população que está sendo
amostrada. Exemplo, regressão do consumo de
eletricidade contra renda (X2) e o tamanho da casa (X3),
há uma restrição física na população, no sentido de que as
famílias com renda mais altas em geral têm casas maiores.
3) Especificação do modelo.
4) Um modelo sobredeterminado. Quando em um modelo
existem mais variáveis que informações.

9. Quebra dos pressupostos:
Multicolinearidade
Estimação na presença de multicolinearidade
Para o modelo
𝑦𝑖 = 𝛽2 𝑥2𝑖 + 𝛽3 𝑥3𝑖 + 𝑢𝑖
Teremos
𝛽2 =
𝑦𝑖 𝑥2𝑖 𝑥3𝑖
2
− 𝑦𝑖 𝑥3𝑖 𝑥2𝑖 𝑥3𝑖
𝑥2𝑖
2
𝑥3𝑖
2
− 𝑥2𝑖 𝑥3𝑖
2
𝛽3 =
𝑦𝑖 𝑥3𝑖 𝑥2𝑖
2
− 𝑦𝑖 𝑥2𝑖 𝑥2𝑖 𝑥3𝑖
𝑥2𝑖
2
𝑥3𝑖
2
− 𝑥2𝑖 𝑥3𝑖
2

10. Quebra dos pressupostos:
Multicolinearidade
Suponha que 𝑋3𝑖 = 𝑋2𝑖
Substituindo na equação teremos:
𝛽2 =
𝑦𝑖 𝑥2𝑖 2 𝑥2𝑖
2
−  𝑦𝑖 𝑥2𝑖  𝑥2𝑖 𝑥2𝑖
𝑥2𝑖
2
2 𝑥2𝑖
2
− 2 𝑥2𝑖 𝑥2𝑖
2
=
0
0
Tanto o estimador beta 2 quanto o beta 3 serão
indeterminados nesse caso.
Agora porque isso acontece?

11. Quebra dos pressupostos:
Multicolinearidade
Devemos lembrar do significado do estimador 𝛽2. Ele nos
fornece a variação do valor médio de Y quando X2 varia uma
unidade, mantendo X3 constante. Porém como X2 e X3 são
uma relação linear perfeita, a medida que um varia o outro
também irá variar, variação esta medida por . Ou seja, não
podemos distinguir diferenças entre o X2 e o X3.
Considerando a relação perfeita entre X2 e X3 podemos
também estabelecer que:
𝑦𝑖 = 𝛽2 𝑥2𝑖 + 𝛽3(𝑥2𝑖) + 𝑢𝑖
𝑦𝑖 = ( 𝛽2 +  𝛽3)𝑥2𝑖 + 𝑢𝑖
𝑦𝑖 = 𝛼𝑥2𝑖 + 𝑢𝑖

12. Quebra dos pressupostos:
Multicolinearidade
Com isso:
𝛼 = 𝛽2 +  𝛽3 =
𝑦𝑖 𝑥2𝑖
𝑥2𝑖
2
Estimação na presença de multicolinearidade “alta”, mas
“imperfeita”
A primeira situação é algo muito raro em se verificar em se
tratando de dados econômicos.
Porém, o que pode ser muito comum é uma colinearidade
entre duas variáveis que seja alta, podemos identificar isso
pela seguinte relação:
𝑥3𝑖 = 𝑥2𝑖 + 𝑣𝑖

13. Quebra dos pressupostos:
Multicolinearidade
Agora, a relação entre X3 e X2 está adicionada a um erro
aleatório v, nesses termos temos, evidentemente, que
considerar que ≠ 0 e 𝑥2𝑖 𝑣𝑖 = 0.
O valor do estimador beta 2 então será
𝛽2 =
𝑦𝑖 𝑥2𝑖 2 𝑥2𝑖
2
+ 𝑣𝑖
2
−  𝑦𝑖 𝑥2𝑖 + 𝑦𝑖 𝑣𝑖  𝑥2𝑖
2
𝑥2𝑖
2
2 𝑥2𝑖
2
+ 𝑣𝑖
2
− 2 𝑥2𝑖
2 2
Agora a equação pode ser estimada. No entanto, conforme
previamente observado, o problema residirá agora no erro
dos estimadores que será supereistimado.

14. Quebra dos pressupostos:
Multicolinearidade
Consequências teóricas da Multicolinearidade
Como foi visto o maior problema da multicolinearidade
ocorrerá apenas, quando ela for perfeita, ou seja, podemos
subentende que a multicolinearidade será um fenômeno que
se apresentará na sua forma “alta” e não perfeita.
Quando ocorre uma alta colinearidade entre duas variáveis
independentes, gerando o efeito da multicolinearidade, os
estimadores poderão, portanto, ser obtidos e eles
conservarão a propriedade sendo não viesados.

15. Quebra dos pressupostos:
Multicolinearidade
Goldber acrescentou outro problema que acarreta em
multicolinearidade, trata-se da micronumerosidade. A mesma
ocorre quando o número de observações é muito próximo ao
número de variáveis no modelo. Poderíamos associar isso ao
exercício feito sobre o capítulo 7, quando o número de
variáveis era igual ao número de observações do modelo,
impedindo o cálculo dos erros padrão dos estimadores e da
variância do resíduo.
Muitas das vezes se é resolvido o problema da
micronumerosidade, aumentando o tamanho da amostra,
resolvemos o problema da multicolinearidade.

16. Quebra dos pressupostos:
MulticolinearidadeConsequências práticas da multicolinearidade
As principais consequências listadas por Gujarati são:
a) Embora sejam MELNT, os estimadores de MQO têm GRANDE
VARIÂNCIAS e COVARIÂNCIAS, tornando difícil uma estimação
precisa e confiante;
b) Devido a consequência (a), os INTERVALOS DE CONFIANÇA
tendem a ser muito mais amplos, levando à aceitação imediata
da “hipótese nula H0” (ou seja, de que o verdadeiro
coeficiente populacional seja igual a zero).
c) Também devido a consequência (a), a razão t de um ou mais
coeficientes tende a ser estatisticamente insignificante.
d) Embora a razão t de um ou mais coeficientes seja
estatisticamente insignificante, o R2, a medida geral da
qualidade do ajustamento, pode ser muito alto.
e) Os estimadores de MQO e seus erros padrão podem ser
sensíveis a pequenas alterações nos dados.

17. Quebra dos pressupostos:
Multicolinearidade
Para exemplificar isso, podemos estabelecer considerando a
fórmula das variâncias que:
𝑣𝑎𝑟 𝛽2 =
𝜎2
𝑥2𝑖
2
1 − 𝑟23
2
𝑣𝑎𝑟 𝛽3 =
𝜎2
𝑥3𝑖
2
1 − 𝑟23
2
E
𝑐𝑜𝑣 𝛽2, 𝛽3 =
𝑟23 𝜎2
1 − 𝑟23
2
𝑥2𝑖
2
𝑥3𝑖
2

18. Quebra dos pressupostos:
Multicolinearidade
Se aplicarmos o limite de 𝑟23 → 1 então teremos:
lim
𝑟23→1
𝑣𝑎𝑟( 𝛽2) = ∞
lim
𝑟23→1
𝑣𝑎𝑟( 𝛽3) = ∞
lim
𝑟23→1
𝑐𝑜𝑣( 𝛽2, 𝛽3) = ∞
Tendo de porte dessa informação, podemos identificar a
velocidade em que esse aumento das variâncias e
covariâncias estão ocorrendo. Tal aspecto ajudou a
implementar o fator de inflação da variância (FIV), que é
definido como:
𝐹𝐼𝑉 =
1
1 − 𝑟23
2

19. Quebra dos pressupostos:
Multicolinearidade
O FIV mostra como a variância de um estimador é inflada pela
presença da multicolinearidade. Quando 𝑟23
2
aproxima-se de
1, o FIV aproxima-se do infinito. Ou seja, quando a
colinearidade aumenta, a variância de um estimador aumenta
e, no limite, pode tornar-se infinita. Se não houver
colinearidade entre X2 e X3 o FIV será 1. Assim as equações
de variância podem ser expressas também a partir do FIV.
𝑣𝑎𝑟 𝛽2 =
𝜎2
𝑥2𝑖
2 𝐹𝐼𝑉
𝑣𝑎𝑟 𝛽3 =
𝜎2
𝑥3𝑖
2 𝐹𝐼𝑉
Que mostra que as variâncias de 𝛽2 e 𝛽3 são diretamente
proporcionais ao FIV.

20. Quebra dos pressupostos:
Multicolinearidade
É mostrada na Tabela 10.1 como evolui a Variância, o FIV e a
Covariância a medida que aumenta-se a colinearidade
(correlação) entre as variáveis X2 e X3.

21. Quebra dos pressupostos:
Multicolinearidade
Então, graficamente o comportamento da variância do
estimador beta 2 tem um comportamento de crescimento
exponencial a medida que a colinearidade se aproxima de 1.

22. Quebra dos pressupostos:
Multicolinearidade
Outro indicado útil utilizado é o TOL, que é conhecido como
TOLERÂNCIA, trata-se da relação inversa da FIV, ou seja:
𝑇𝑂𝐿𝑗 =
1
𝐹𝐼𝑉𝑗
= (1 − 𝑅𝑗
2
)
Ou seja, quando 𝑅𝑗
2
= 1 (colinearidade perfeita), 𝑇𝑂𝐿𝑗 = 0 e
𝑅𝑗
2
= 0 (ausência de colinearidade), 𝑇𝑂𝐿𝑗 = 1.

23. Quebra dos pressupostos:
Multicolinearidade
INTERVALOS DE CONFIANÇA MAIS AMPLOS.
Dado os erros padrão grandes, os intervalos de confiança dos
parâmetros populacionais relevantes tendem a ser maiores,
como podemos ver na Tabela 10.2 abaixo.

24. Quebra dos pressupostos:
Multicolinearidade
Por exemplo, quando 𝑟23 = 0,95, o intervalo de confiança
para 𝛽2 é maior que quando 𝑟23 = 0 por um fator de 10,26,
ou cerca de 3.
Dessa forma, em casos de alta multicolinearidade, os dados
da amostra podem ser compatíveis com um conjunto diverso
de hipóteses. A probabilidade de aceitar uma hipótese falsa
(erro tipo II) aumenta.

25. Quebra dos pressupostos:
Multicolinearidade
RAZÕES t “INSIGNIFICANTES”
Ou seja, individualmente a estatística t é importante para se
verificar a significância do estimador, pois, 𝑡 = 𝛽𝑖/𝑒𝑝( 𝛽𝑖).
Porém, podemos observar que diante da multicolinearidade,
os erros padrão aumentam consideravelmente, tornando os
valores t menores. Em tais casos, aceita-se cada vez mais a
hipótese nula de que o verdadeira valor populacional é zero.

26. Quebra dos pressupostos:
Multicolinearidade
ALTO VALOR DE 𝑅2
, MAS POUCA RAZÕES t SIGNIFICATIVAS.
Vamos considerar o modelo de regressão linear com k
variáveis:
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋2𝑖 + 𝛽3 𝑋3𝑖 + ⋯ + 𝛽 𝑘 𝑋 𝑘𝑖 + 𝑢𝑖
Em casos de alta colinearidade, é possível constatar, como já
verificado anteriormente, que um ou mais coeficientes
angulares parciais são não significantes individualmente,
baseado no teste t. Nessas situações, o 𝑅2
pode ser tão alto,
como 0,9, que de acordo como teste F podemos rejeitar
convicentemente a hipótese de que 𝛽2 = 𝛽3 = ⋯ = 𝛽 𝑘 = 0.
De fato, esse é um dos indícios de multicolinearidade.

27. Quebra dos pressupostos:
Multicolinearidade
SENSIBILIDADE DOS ESTIMADORES DE MQO E DE SEUS ERROS
PADRÃO A PEQUENAS ALTERAÇÕES NOS DADOS.
Considerando uma alta colinearidade (e não a perfeita), é
possível estimar os coeficientes de regressão, mas as
estimativas e seus erros padrão tornam-se muito sensíveis até
mesmo à menor alteração nos dados.
O autor faz uso de uma tabela com 5 informações, onde são
alteradas apenas a ordem de algumas observações da variável
X3. Trata-se das tabelas 10.3 e 10.4.
No slide a seguir encontram-se as tabelas e as estimativas
antes e depois da modificação dos dados:

28. Quebra dos pressupostos:
Multicolinearidade
Os Resultados de cada modelo são:

29. Quebra dos pressupostos:
Multicolinearidade
Detecção da MULTICOLINEARIDADE
Segundo Kmenta:
1 – A multicolinearidade é uma questão de grau e não de
tipo. A distinção significativa não é entre a presença e a
ausência da mesma, mas entre seus vários graus.
2 – Uma vez que a multicolinearidade refere-se à condição
das variáveis explanatórias que se supõe não serem
estocásticas, ela é uma característica da amostra, e não da
população.
Ou seja, não são realizado testes para a multicolinearidade,
mas é medido o grau da multicolinearidade em uma amostra
específica.

30. Quebra dos pressupostos:
Multicolinearidade
Com isso, podemos estabelecer algumas observações ou
regras a serem utilizadas para identificar a presença o
fenômeno da multicolinearidade em uma amostra de dados.
Vejamos os principais:
1) 𝑅2 alto, mas poucas razões t significativas. É um dos mais
clássicos e diretos sintomas da presença da
Multicolinearidade. Evidencia-se como 𝑅2 alto aqueles
com valor acima de 0,8.
2) Altas correlações entre os pares das variáveis
independentes. Se for observadas correlações acima de
0,8 entre os regressores, devemos ligar o sinal de alerta
sobre a presença da multicolinearidade.

31. Quebra dos pressupostos:
Multicolinearidade
3) Regressões auxiliares. É uma das verificações mais comuns,
trata-se de uma forma de se descobrir qual variável X está
mais relacionada a outras variáveis X. A dinâmica do teste
consiste em tirarmos a variável dependente do modelo (Y) e
elencar (de forma alternada) outra variável independente e
utiliza-la como dependente contra as demais em um novo
modelo. Se o R2 desse novo modelo for maior que o R2 do
modelo que inclui a variável Y, então há fortes indícios da
presença da multicolinearidade.

32. Quebra dos pressupostos:
Multicolinearidade
Se tivermos o seguinte modelo:
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋2𝑖 + 𝛽3 𝑋3𝑖 + 𝛽4 𝑋4𝑖 + 𝑢𝑖
𝑅 𝑦
2
E
𝑋2𝑖 = 𝛼1 + 𝛼2 𝑋3𝑖 + 𝛼3 𝑋4𝑖 + 𝑣𝑖
𝑅 𝑋2
2
Se o 𝑅 𝑋2
2
> 𝑅 𝑦
2, então temos forte evidência da existência da
Multicolinearidade.
Tal regressão pode ser ainda feita considerando as outras
variáveis X (X3 e X4) como variáveis dependentes.

33. Quebra dos pressupostos:
Multicolinearidade
4) TOL e FIV.
5) Diagrama de dispersão.

34. Quebra dos pressupostos:
Multicolinearidade

35. Quebra dos pressupostos:
Multicolinearidade
Medidas Corretivas
Deixa para lá (Não fazer nada). Gujarati remete a um exemplo
do Blanchard indicando que a multicolinearidade é algo
inerente dos dados (Micronumerosidade) e muitas das vezes
não temos escolha sobre os dados disponíveis para a análise
empírica.
1) Ter uma informação a priori. É tratado o exemplo sobre
consumo (Y) sendo afetado por riqueza (X2) e renda (X3). Ora,
se temos a informação de que há um forte grau entre as
variáveis X2 e X3, porque manter as duas no modelo, basta
rodar o modelo apenas com uma. O conhecimento de vasta
literatura é que nos propicia diversos elementos para definir
se duas variáveis específicas irão relacionar a algo comum ou
não.

36. Quebra dos pressupostos:
Multicolinearidade
2) Combinar dados de corte transversal com séries de tempo.
Esse tipo de medida é uma tentativa de aumentar o número
de observações na amostra. Empilhar os dados dessa forma é
conhecido como montagem de um painel.
3) Exclusão de variável(is) e viés de especificação. Excluir uma
das variáveis que está causando a colinearidade é a saída
mais comum adotada por quem modela. Porém, em algumas
situações essa decisão nos leva a tomar decisões polêmicas.
Um dos exemplos citados no livro e a relação que pode existir
entre renda e riqueza. Se a teoria econômica informa que
essas variáveis devem ser estimadas em conjunto, e verifica-
se que ambas possuem forte correlação (colinearidade) então
o que devemos atender, a situação em que a teoria define a
presença da mesma, ou então tirar a variável do modelo?

37. Quebra dos pressupostos:
Multicolinearidade
Quando acontece esse empasse, o que permite mantes duas
variáveis no mesmo modelo e a transformação das mesmas.
4) Transformação de variáveis. Usar artifícios como tirar o log,
definir uma primeira diferença, ou ate estipular uma
transformação proporcional são artifícios que podem ser
utilizados para modificar variáveis do modelo.
5) Inserir novos dados. É um artifício muito interessante, no
entanto inserir novas informações na amostra pode se
mostrar um processo caro e demorado, o que torna algo
pouco comum de ser feito.

38. Quebra dos pressupostos:
Multicolinearidade
6) Reduzindo a colinearidade em regressões polinomiais;
7) Uso da análise multivariada para criação de fatores.

39. Quebra dos pressupostos:
Multicolinearidade
Exemplo: Uso dos dados de Longley.
No Gretl será realizado a partir da tabela 10.7, a mesma
estará disponível no mediafire com o nome “Gujarati - Tabela
10.7 - Dados de Longley.gdt”

40. FIM DO TÓPICO
3