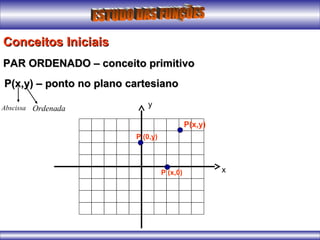
1. Conceitos IniciaisConceitos Iniciais
PAR ORDENADO – conceito primitivoPAR ORDENADO – conceito primitivo
P(x,y) – ponto no plano cartesianoP(x,y) – ponto no plano cartesiano
Abscissa Ordenada
P(x,y)
P (x,0)
P (0,y)
x
y

2. FUNÇÃOFUNÇÃO
DEFINIÇÃODEFINIÇÃO
Sejam A e B dois conjuntos não vazios e uma relação R de ASejam A e B dois conjuntos não vazios e uma relação R de A
em B, essa relação será chamada de função quandoem B, essa relação será chamada de função quando parapara
todotodo e qualquer elemento de A estiver associado ae qualquer elemento de A estiver associado a um únicoum único
elemento em B.elemento em B.
A relação binária h = {(x;y)| y < x}A relação binária h = {(x;y)| y < x}
xy <
A B2
4
1
3
5
h: {(2;1), (4;1), (4,3)}h: {(2;1), (4;1), (4,3)}
A relação binária g = {(x;y)| y= x + 3}A relação binária g = {(x;y)| y= x + 3}
3+= xy
2
4
1
3
5
g: {(2;5)}g: {(2;5)}
A B
NÃO É FUNÇÃONÃO É FUNÇÃO NÃO É FUNÇÃONÃO É FUNÇÃO

3. c) A relação binária f = {(x;y)| y = x + 1}c) A relação binária f = {(x;y)| y = x + 1}
1+= xy
A B2
4
1
3
5
f: {(2;3), (4;5)}f: {(2;3), (4;5)}
f é uma função de A em B, poisf é uma função de A em B, pois todotodo
elemento de A está associado aelemento de A está associado a um únicoum único
elemento em Belemento em B
ELEMENTOS DE UMA FUNÇÃO: f: AELEMENTOS DE UMA FUNÇÃO: f: A →→ BB
DOMÍNIO: A = {2, 4}DOMÍNIO: A = {2, 4}
CONTRA DOMÍNIO: B = {1, 3, 5}CONTRA DOMÍNIO: B = {1, 3, 5}
CONJUNTO IMAGEM: Im (f) = {3, 5}CONJUNTO IMAGEM: Im (f) = {3, 5}

4. Não é função
CONTRA EXEMPLO DE FUNÇÃOCONTRA EXEMPLO DE FUNÇÃO

5. Considere a função f: AConsidere a função f: A →→ B definida por y = 3x + 2, pode-seB definida por y = 3x + 2, pode-se
afirmar que o conjunto imagem de f é:afirmar que o conjunto imagem de f é:
23 += xy
A B 23 += xy
521.3 =+=y1
2
3
5
8
11
15
17
822.3 =+=y
1123.3 =+=y
23)( += xxf
→
→
→
5)1( =f
8)2( =f
11)3( =f
}11,8,5{)Im( =∴ f

6. GRÁFICO DA FUNÇÃO f: AGRÁFICO DA FUNÇÃO f: A →→ B definida por y = 3x + 2B definida por y = 3x + 2
Pares Ordenados Obtidos: {(1,5); (2,8); (3,11)}Pares Ordenados Obtidos: {(1,5); (2,8); (3,11)}
1 2 3
11
8
5
x
y

7. 1 2 3
11
8
5
x
y
GRÁFICO DA FUNÇÃO f:GRÁFICO DA FUNÇÃO f: ℜℜ →→ ℜℜ definida por y = 3x + 2definida por y = 3x + 2

8. Seja o gráfico abaixo da função f, determinar a soma dos números associados às
proposições VERDADEIRAS:
01. O domínio da função f é {x ∈ R | - 3 ≤ x ≤ 3}
02. A imagem da função f é {y ∈ R | - 2 ≤ y ≤ 3}
04. para x = 3, tem-se y = 3
08. para x = 0, tem-se y = 2
16. para x = - 3, tem-se y = 0
32. A função é decrescente em todo seu domínio
V
V
(3,3) ou f(3) = 3
(0,2) ou f(0) = 2
(-3,2) ou f(-3) = 2
V
V
F
F

9. y = f(x) = ax +
b
a > 0
y
D = ℜ Im = ℜ
FUNÇÃO
CRESCENTE
(0, b)
x
y
(0, b)
x
FUNÇÃO
DECRESCENTE
a < 0
Raiz ou
zero da
função
y = 0

10. y = x – 2
y
(0, -2)
x2 3
1
4
2
5
3
y = 3x –
6
y
(0, -6)
x2 3
3
4
6
5
9
CÁLCULO DO COEFICIENTE ANGULAR – TAXA DE VARIAÇÃO
Δx
Δy
a =

11. Seja f(x) = ax + b. Sabe-se que f(3) = 5 e f(-1) = - 3. Dê o valor de f(8).
f(3) = 5
f(-1) = -3
(3, 5)
(-1, -3)
y = ax + b
5 = a(3) + b
-3 = a(-1) + b



=+
=+
3-ba-
5b3a
a = 2 b = - 1
f(x) = ax + b
f(x) = 2x – 1
Logo: f(8) = 2.8 – 1 f(8) = 15

12. O valor de uma máquina decresce linearmente com o tempo, devido ao desgaste.
Sabendo-se que hoje ela vale R$800,00, e que daqui a 5 anos valerá R$160,00,
o seu valor, em reais, daqui a três anos será:
x(anos)
y(reais)
0 5
160
800
Função do 1º grau:
f(x) = a.x+ b
P1(0,800)
P2(5,160)
800 = a.0 + b
b = 800
160 = a. 5 + 800
-640 = 5a
a = -128
f(x) = a.x+ b
f(x) = -128.x+ 800
f(3) = -128.3+ 800
f(3) = 416f(3) = 416
Portanto após 3 anos a
Máquina valerá R$ 416,00

13. A semi-reta representada no gráfico seguinte expressa o custo de produção C, em
reais, de n quilos de certo produto.
C(reais)
x(quilogramas)0 20
80
180
Se o fabricante vender esse
produto a R$ 102,00 o quilo,
a sua porcentagem de lucro
em cada venda será?
Função do 1º grau:
f(x) = a.x+ b
P1(0,80)
P2(20,180)
80 = a.0 + b
b = 80
180 = a. 20 + 80
20a = 100
a = 5
f(x) = a.x+ b
f(x) = 5.x+ 80
f(1) = 5.1+ 80 ⇒⇒ f(1) = 85f(1) = 85
R$ 85 ⇔ 100%
R$102 ⇔ x
x = 120%
LUCRO DE 20%

15. Um camponês adquire um moinho ao preço de R$860,00. Com o passar do tempo,
ocorre uma depreciação linear no preço desse equipamento. Considere que, em 6 anos,
o preço do moinho será de R$ 500,00. Com base nessas informações, é correto afirmar:
x(anos)
y(reais)
0 6
500
860
Função do 1º grau:
f(x) = a.x+ b
A(0,860)
B(6,500)
860 = a.0 + b
b = 860
500 = a. 6 + 860
-360 = 6a
a = -60
f(x) = a.x+ b
f(x) = -60.x+ 860
a) f(3) = -60.3+ 860
f(3) = 680
A
B
F
b) f(9) = -60.9+ 860
f(9) = 320
F
c) f(7) = -60.7+ 860
f(7) = 440
F
d) - 60x + 860 < 200
-60x < -660
x > 11anos
F
e) f(13) = -60.13+ 860
f(13) = 440
f(13) = 80
V

16. Em um termômetro de mercúrio, a temperatura é uma função afim (função do 1o
grau) da altura do mercúrio. Sabendo que as temperaturas 0o
C e 100o
C
correspondem, respectivamente, às alturas 20 ml e 270 ml do mercúrio, então a
temperatura correspondente a 112,5 ml é
ml
temperatura0 100
20
270
Função do 1º grau:
f(x) = a.x+ b
P1(0,20)
P2(100,270)
20 = a.0 + b
b = 20
270 = a. 100 + 20
100a = 250
a = 2,5
f(x) = a.x+ b
f(x) = 2,5.x+ 20
y = 2,5x + 20
112,5 = 2,5x + 20
92,5=2,5x
37°C = x

17. y = f(x) = ax2
+ bx
+ c
Vértice
(0,c)
xV
yV
x1 x2
Vértice
(0,c)
xV
yV
x1
x2
y
x x
y
a > 0 a < 0
Raízes : xRaízes : x11 e xe x22
ax2
+ bx + c = 0 2 4
V V
b
x e y
a a
− −∆
= =

18. Após o lançamento de um projétil, sua
altura h, em metros, t segundos após o
seu lançamento é dada por
h(t) = – t2
+ 20t. Em relação a este
lançamento, analise as afirmações a
seguir.
l. A altura máxima atingida pelo projétil
foi de 10m.
ll. O projétil atingiu a altura máxima
quando t=10s.
lll. A altura do projétil é representada por
uma função polinomial quadrática cujo
domínio é [0,20].
lV. Quando t = 11, o projétil ainda não
atingiu sua altura máxima.
Todas as afirmações corretas estão em:
a) I – III b) I – II – IV c) II – III d) III –
IV
ACAFE - 2010 PUC – PR - 2010
O lucro de uma determinada
empresa é dado pela lei
L(x) = -L(x) = - xx22
+ 8+ 8xx - 7- 7, em que x é a
quantidade vendida (em milhares de
unidades) e L é o lucro (em reais). A
quantidade que se deve vender para
que o lucro seja máximo bem como
o valor desse lucro são,
respectivamente:
A) 3.000 unidades e R$ 6.000,00
B) 4.000 unidades e R$ 9.000,00
C) 4.000 unidades e R$ 8.000,00
D) 5.000 unidades e R$ 12.000,00
E) 4.500 unidades e R$ 9.000,00

19. UFSC - 2009
Se o lucro de uma empresa é dado por
L(x) = 4(3 – x)(x – 2), onde x é a
quantidade vendida, então o lucro da
empresa é máximo quando x é igual a:
UFSC - 2013
O lucro, em reais, para a comercialização
de x unidades de um determinado
produto é dado por
L(x) = - 1120 + 148x – x2
. Então, para
que se tenha lucro máximo, deve-se
vender quantos produtos?
UFSC - 2005
Tem-se uma folha de cartolina
com forma retangular, cujos lados
medem 56cm e 32cm e deseja-
se cortar as quinas, conforme
ilustração a seguir. Quanto
deve medir x, em centímetros,
para que a área da região
hachurada seja a maior possível?
GABARITO: 11

20. As dimensões de um retângulo são dadas em centímetros, pelasAs dimensões de um retângulo são dadas em centímetros, pelas
expressões: 2x e (10 – 2x) com 0 < x < 5. Determinar, neste caso, o valorexpressões: 2x e (10 – 2x) com 0 < x < 5. Determinar, neste caso, o valor
máximo da área em cmmáximo da área em cm22
, que esse retângulo pode assumir., que esse retângulo pode assumir.
Vértice
5/2
yV
0 5
2x
10 – 2x
A = base x altura
A = 2x . (10 – 2x)
A(x) = – 4x2
+ 20x
a = - 4 b = 20 c = 0
RAÍZES OU ZEROS DA FUNÇÃO
0 = – 4x2
+ 20x
x2
- 5x = 0
x1 = 0 x2 = 5
Área
Área Máxima é o yv
A(5/2) = – 4(5/2)2
+ 20(5/2)
A(5/2) = 25cm2

21. RESUMO GRÁFICO
∆ > 0
x1 ≠ x2
x1 x2
y
x
∆ = 0
x1 = x2
x1 = x2
x
y
∆ < 0
x1, x2 ∉ R
x
y

22. 04)
GABARITO: 1/2

23. 05)
GABARITO: E

24. 06)
GABARITO: E

25. a)

27. Considere o triângulo ABC, com base BC medindo 6cm e com altura 5cm. Um
retângulo inscrito nesse triângulo tem o lado MN paralelo a BC, com x cm de
comprimento. Qual o valor de x, em cm, para que a área do retângulo seja
máxima?

28. FUNÇÃO PAR OU ÍMPARFUNÇÃO PAR OU ÍMPAR
FUNÇÃO PAR
VALORES SIMÉTRICOS DE X
IMAGENS IGUAIS
f(x) = x2
– 4
f(-3) = (-3)2
– 4 =
f(3) = (3)2
– 4 =
5
5
FUNÇÃO ÍMPAR
VALORES SIMÉTRICOS DE X
IMAGENS SIMÉTRICAS
f(x) = x3
f(-4) = (-4)3
=
f(4) = 43
=
- 64
64
f(-x) = f(x) f(-x) = - f(x)

29. FUNÇÃO PAR
VALORES SIMÉTRICOS DE X
IMAGENS IGUAIS
FUNÇÃO ÍMPAR
VALORES SIMÉTRICOS DE X
IMAGENS SIMÉTRICAS
f(-x) = f(x)
f(-x) = - f(x)
FUNÇÃO PAR OU ÍMPAR?FUNÇÃO PAR OU ÍMPAR?
1) f(x) = 4x3
+ x
GRÁFICO SIMÉTRICO AO EIXO Y
GRÁFICO SIMÉTRICO EM RELAÇÃO
A ORIGEM
2) f(x) = 3x4
+ 5x2
3) f(x) = 5x4
+ 2x3
4) f(x) = sen x
5) f(x) = cos x
6) f(x) = tg x
ÍMPARÍMPAR f(-x) = - f(x)
f(-2) = - f(2)
PARPAR f(-x) = f(x)
f(-3) = f(3)
SEMSEM
PARIDADEPARIDADE
ÍMPARÍMPAR sen(-x) = - sen(x)
sen(-30°) = - sen(30°)
PARPAR
cos(-x) = cos(x)
cos(-30°) = cos(30°)
ÍMPARÍMPAR tg(-x) = - tg(x)
tg(-30°) = - tg(30°)

30. UFSC 2013UFSC 2013
f é uma função ÍMPAR?f é uma função ÍMPAR?
NÃO, POIS f(-2)NÃO, POIS f(-2) ≠ -f(2)≠ -f(2)

31. Observe o gráfico da função cujo domínio é o conjunto
D={x∈ R/- 2 < x < 4} e analise as afirmações a seguir.
ACAFE 2013.1ACAFE 2013.1
l. A função é par.
ll. A função possui 3 raízes reais.
lll. No intervalo A=[1,3] a função é
decrescente.
IV. A função pode ser representada por
y = x³ - 3x² -x +3,
sendo D={x∈ R/- 2 <
x < 4}
Todas as afirmações corretas estão em:
a) I - II - III
b) II - IV
c) II - III - IV
d) III - IV

32. ( ) 34xxg −= ( ) 12xxf +=
A B C
FUNÇÃO COMPOSTAFUNÇÃO COMPOSTA
f(g(x)) = fog (x)
g(f(x)) = gof (x)
f(f(x)) = fof(x)
g(g(x)) = gog(x)
NOTAÇÕESNOTAÇÕES
2 5 11
( ) 5-8xg(x)f =
f(x) = 2x + 1
f(…) = 2(…) + 1
f(g(x)) = 2g(x) + 1
f(g(x)) = 2(4x – 3) + 1
CÁLCULO de f(g(x))CÁLCULO de f(g(x))
f(g(x)) = 8x – 5

33. FUNÇÃO COMPOSTAFUNÇÃO COMPOSTA
Sejam f(x) = 2x + 3, g(x) = x – 5 e h(x) = 3x – 1. Calcule f(g(h(3))
f(x) = 2x + 3 g(x) = x – 5 h(x) = 3x – 1
h(3) = 3.3 – 1
h(3) = 9 – 1
h(3) = 8
g(8) = 8 – 5
g(8) = 3
f(3) = 2.3 + 3
f(3) = 6 + 3
f(3) = 9
Portanto f(g(h(3)) = 9

34. O número N de caminhões produzidos em uma montadora durante um
dia, após t horas de operação, é dado por N(t) = 20t – t2
, sendo que 0 ≤ t ≤
10. Suponha que o custo C (em milhares de reais) para se produzir N
caminhões seja dado por C(N) = 50 + 30N.
a) Escreva o custo C como uma função do tempo t de operação da
montadora.
b) Em que instante t, de um dia de produção, o custo alcançará o valor de
2300 milhares de reais?
UFPR – 2013 – SEGUNDA FASEUFPR – 2013 – SEGUNDA FASE

35. UFSC – VERDADEIRO OU FALSOUFSC – VERDADEIRO OU FALSO
Sejam f e g funções reais definidas por f(x) = sen x e g(x) = x2
+ 1.
Então (fog)(x) = (fog)(– x) para todo x real.
UFSC 2012UFSC 2012
VV
Sejam h e k, duas funções, dadas por h(x) = 2x - 1 e k(x) = 3x + 2.
Então h(k(1)) é igual a 9.
UFSC 2002UFSC 2002
VV
UFSC 2006UFSC 2006
UFSC – QUESTÃO ABERTAUFSC – QUESTÃO ABERTA

36. GABARITO: B

37. FUNÇÃO INJETORAFUNÇÃO INJETORA
GRÁFICO ESTRITAMENTE CRESCENTE OU ESTRITAMENTE DECRESCENTE
FUNÇÃO SOBREJETORAFUNÇÃO SOBREJETORA
FUNÇÃO BIJETORAFUNÇÃO BIJETORA

38. UFSC 2013UFSC 2013
f é uma função INJETORA?f é uma função INJETORA?
NÃO, POIS f(2,3) =NÃO, POIS f(2,3) = f(2,7)f(2,7)

39. FUNÇÃO INVERSAFUNÇÃO INVERSA
3x
1-2x
f(x)
−
=
Encontre a inversa da função
3x
1-2x
f(x)
−
=
x =
3
12
−
−
y
y
x(y – 3) = 2y – 1
xy – 3x = 2y – 1
xy – 2y = 3x – 1
xy – 2y = 3x – 1
y(x – 2) = 3x – 1
y =
2
13
−
−
x
x
2x
13x
(x)f 1
−
−
=−
GABARITO: 27