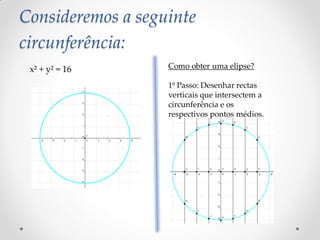
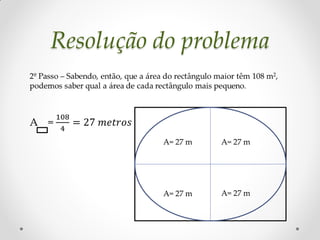
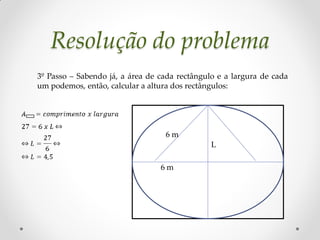
Este documento discute a elipse matemática. Apresenta a origem histórica da elipse com Apolônio de Perga no século II a.C. e descreve as propriedades e componentes da elipse, incluindo focos, vértices e eixos. Também fornece exemplos de como construir elipses geometricamente e resolve dois problemas relacionados a elipses.

1. Trabalho de grupo nº1 de
Matemática
Proposta nº8
2011/2012
Profº: Luís Vilhena & Emília Santos
Trabalho realizado por: Beatriz Cabrita nº3
Bruno Cardoso nº6

2. Recuando no tempo…
Na origem da Elipse estiveram
envolvidos variados matemáticos, mas o
que mais se destacou foi Apolónio de
Perga, um matemático e astrónomo grego
(262 a.C. - 190 a.C.).
Apolônio escreveu oito livros
dedicados especialmente ao estudo de uma
família de curvas - cônicas.

3. As cônicas são curvas que se obtêm intersectando
uma superfície cónica com um plano. Desse modo,
só pode haver quarto tipos de cortes resultantes
desse processo :
• A Círculo
• A Elipse
• A Parábola
• A Hipérbole

4. Aplicações da elipse
φ A elipse é frequentemente usada na
Arquitectura, no Design e na
Engenharia.
φNos auditórios, nos teatros e nas
igrejas são utilizadas porque têm
propriedades que criam condições
acústicas especiais.
φNo século XVII Johannes Kepler
descobriu que a órbita dos planetas do
sistema solar é uma elipse e o sol ocupa
um de seus focos.

5. Mas afinal, o que é uma elipse?
Elipse é o lugar geométrico dos pontos
do plano tais que a soma das distâncias a dois
pontos fixos (focos) é constante e maior que a
distância entre eles.
__ __
KA+KB= constante
___ ___ Foco
HA+BH= constante Foco
___
E maior que AB

6. Como obter uma eclipse a partir de duas
circunferências?
geogebra 1.ggb
Barra de Reprodução
EXEMPLO
Se quisermos construir uma elipse cuja soma das distâncias aos
focos F(-4.0) e F’(4.0) seja 12, podemos fazê-lo através de duas
circunferências com centro nos focos. A soma dos seus raios tem
de ser igual a 12:
(x+4)² + y² = 36 e (x-4)² + y² = 36
(x+4)² + y² = 64 e (x-4)² + y² = 16
(x+4)² + y² = 9 e (x-4)² + y² = 81
…
As intersecções destas circunferências são pontos da elipse.

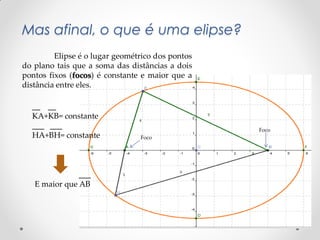
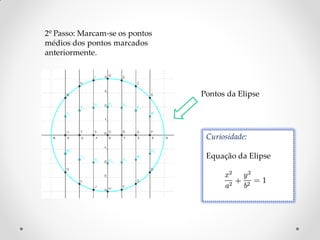
7. Componentes da Elipse:
Dois Focos (F e F’);
Vértice
Eixo Maior [AA’];
Eixo Menor [BB’];
Distância Focal FF’
¯¯;
Vértices (A, A’, B ,B’)

8. Sobre a elipse…
• A distância entre um foco e um dos vértices da elipse é
metade do eixo maior.

9. Consideremos a seguinte
circunferência:
x² + y² = 16 Como obter uma elipse?
1º Passo: Desenhar rectas
verticais que intersectem a
circunferência e os
respectivos pontos médios.

10. 2º Passo: Marcam-se os pontos
médios dos pontos marcados
anteriormente.
Pontos da Elipse
Curiosidade:
Equação da Elipse

11. Podemos construir duas elipses diferentes:
Se o eixo maior for o das Se o eixo maior foi o das
abcissas: ordenadas:

12. 1º Problema

13. Resolução do problema
1º Passo: Constroem-se duas circunferências com centro nos focos da elipse e
raio 6 cada uma, porque a soma das distâncias dos focos a um ponto da elipse é
12 e metade é 6. O raio das circunferências tem de ser 6.
2º Passo: Na intersecção das duas circunferências definimos 2 pontos.

14. Resolução do problema
3º Passo – Constrói-se a elipse sendo que os seus focos são (-4,0) e (4,0) e os
seus vértices são as intersecções das circunferências.

15. Resolução do problema
4º Passo – Sendo o raio das circunferências 6 então, sabemos que a distância
de é igual a 6.

16. 2º Problema

17. Resolução do problema
Tal como mencionámos anteriormente, a distância entre um foco e um dos
pontos da elipse é metade do eixo maior, assim sendo, como a corda
utilizada tinha 12 metros, o eixo maior têm 12 metros.
1º Passo – Divide-se o a figura em 4 partes iguais obtendo 4 rectângulos.
12 m

18. Resolução do problema
A= 27 m A= 27 m
A= 27 m A= 27 m

19. Resolução do problema
3º Passo – Sabendo já, a área de cada rectângulo e a largura de cada
um podemos, então, calcular a altura dos rectângulos:
6m
L
6m

20. Resolução do problema
4º Passo – Podemos concluir que a largura do rectângulo, onde está
inscrita uma elipse, têm 12 metros de largura e 9 metros de altura. A
partir destes dados podemos calcular o perímetro do rectângulo para
saber quantos metros de rede precisa o jardineiro para vedar o canteiro.
P = 12 +12 + 9 + 9
P = 42 metros
9m
Resposta: O jardineiro não
têm rede suficiente para 12 m
vedar o canteiro e para que
tal aconteça precisa de 42
metros.

21. FIM