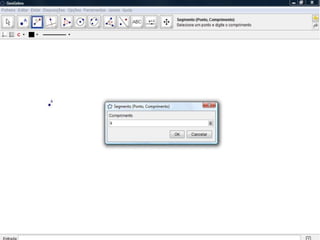
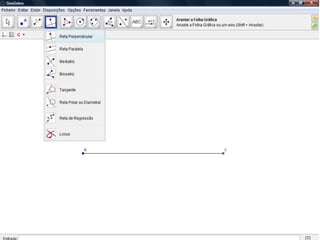
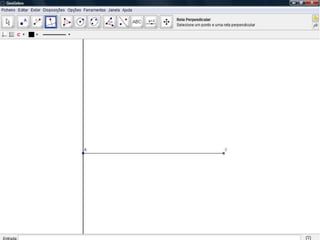
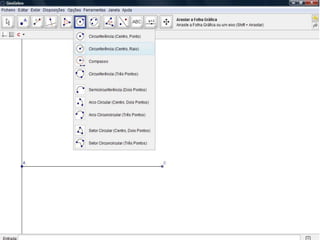
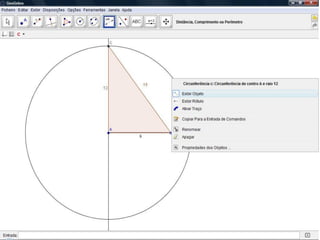
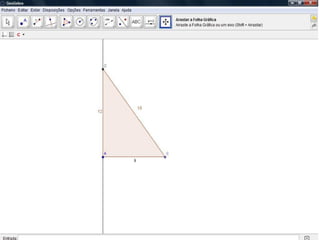
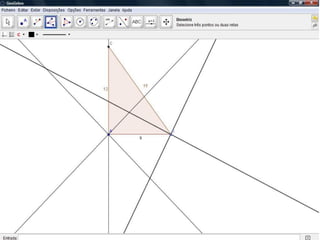
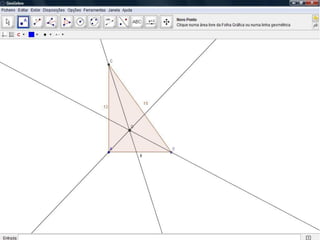
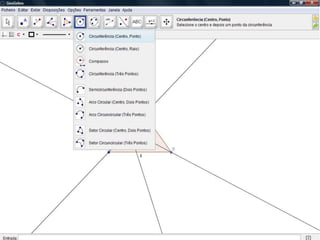
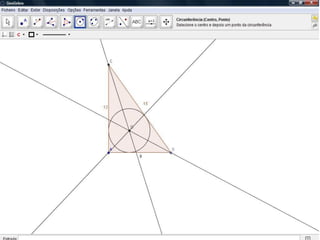
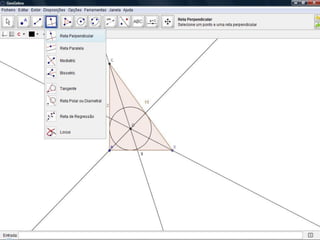
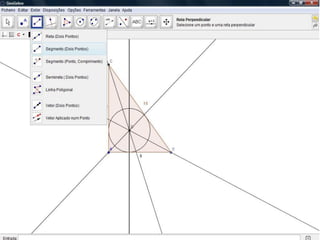
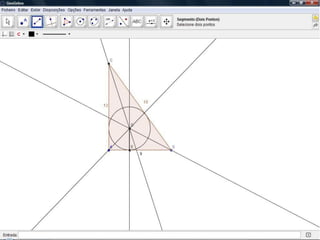
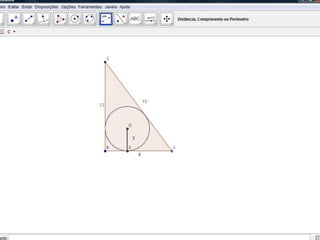
O documento descreve como resolver um problema matemático para encontrar o raio de uma circunferência inscrita em um triângulo. Ele explica como usar o teorema de Pitágoras e a área do triângulo para descobrir que, dados os lados de 9 cm e 12 cm e a hipotenusa de 15 cm, o raio da circunferência é de 3 cm.

1. 2.
O Raio da Circunferência Inscrita
Disciplina de Matemática
Docente: Prof. Luís Vilhena & Emilia Santos
Discentes: Catarina Duarte nº6;
Raquel Duarte nº19;
10ºB 6/12/2011

2. 2. O Raio da Circunferência Inscrita
Introdução

3. 2. O Raio da Circunferência Inscrita
Resolução analítica
Sabemos que,
o perímetro do triângulo é 36 cm;
a hipotenusa do triângulo é 15 cm;
Perímetro do triângulo

4. 2. O Raio da Circunferência Inscrita
Resolução analítica
Para descobrir-mos o X e o Y temos de ir
experimentando vários números até ver se a soma do X
com o Y dá 21.
Por exemplo:
 se o X for 10 e o Y for 11, vai dar 21;
 mas temos de ver, se o X e o Y ao quadrado dão 225
(152) no teorema de Pitágoras.

5. 2. O Raio da Circunferência Inscrita
Resolução analítica
O número 10 e o número 11 dão 21, mas não dão 225, logo
o X e o Y não são nem 10, nem 11.

6. 2. O Raio da Circunferência Inscrita
Resolução analítica
Já vimos que o 10 e 0 11 não dão.
Então agora vamos experimentar com o 9 e com o 12.
A soma do número 9 e o número 12, dá 21.

7. 2. O Raio da Circunferência Inscrita
Resolução analítica
Número 9 e o número 12 são a resposta do problema.

8. 2. O Raio da Circunferência Inscrita
Resolução analítica
Agora que já descobrir-mos o X e o Y, podemos encontrar
o raio da circunferência.
Para descobrir-mos o raio temos de fazer a área do
triângulo.

9. 2. O Raio da Circunferência Inscrita
Resolução analítica
O raio é a altura do três triângulos logo,

10. 2. O Raio da Circunferência Inscrita
Resolução no Geogebra

37. Conclusão
Depois de realizarmos o problema proposto ficámos a
saber que o X e o Y tomavam o valor de 12 cm e 9 cm, a
partir da descoberta desses resultado s conseguimos
obter o valor do raio, que era 3 cm.

38. Fim