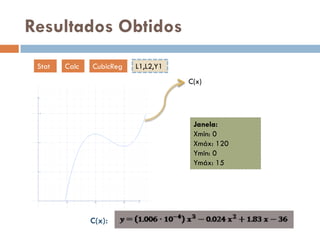
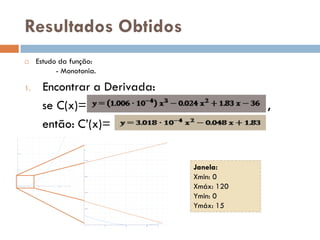
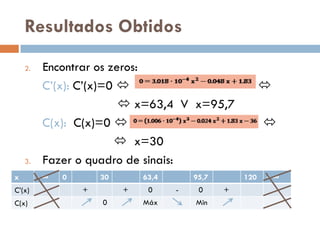
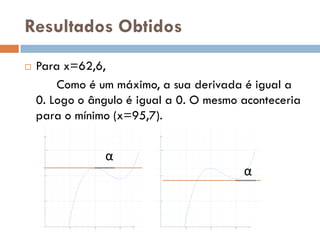
Este documento analisa o consumo de gasolina de um carro Opel em diferentes velocidades entre 40-120 km/h. Ele encontra uma função cúbica para modelar o consumo, estuda a derivada da função para determinar pontos de máximo e mínimo consumo, e conclui que o carro é mais eficiente a velocidades entre 63,4-95,7 km/h, especialmente próximo a 95,7 km/h.

1. Escola Secundária de Pinheiro e Rosa
Matemática A – 11ºB
Ana Fernandes nº1
TRABALHO INDIVIDUAL DE
MATEMÁTICA
Professor:
Rui Lopes
“Consumo de Gasolina”

2. Índice
 Índice
 Introdução
 Metodologia utilizada para a recolha e
tratamento dos dados estatísticos
 Resultados Obtidos
 Conclusões
 Elementos Consultados

3. Introdução
 O trabalho é baseado na aplicação de conteúdos
aprendidos na aula sobre funções, derivadas de
funções, estudo da monotonia através de um
problema real. Este trabalho visa demonstrar a
importância do tema que estudamos este período e
a sua aplicação ao real/quotidiano.

4. Introdução:
 Função: Uma função é uma lei segundo a qual,
para cada elemento x em um conjunto A
corresponde um único elemento y em um conjunto B.
 Derivada: A derivada de uma função y = f(x) num
ponto x = x0 , é igual ao valor da tangente
trigonométrica do ângulo formado pela tangente
geométrica à curva representativa de
y=f(x), no ponto x = x0, ou seja, a derivada é o
coeficiente angular da recta tangente ao gráfico
da função no ponto x0.

5. Metodologia utilizada para a recolha
e tratamento dos dados estatísticos
 Com base no tema “Introdução ao Cálculo
Diferencial. Funções racionais e com radicais.
Taxa Média de variação e derivada”, e
recorrendo a valores reais, foi feito um estudo
da do consumo de gasolina de um carro a
partir de um estudo previamente feito.

6. Problema
 Devido ao aumento dos preços da gasolina, é
necessário, hoje em dia, obter um carro cujo
rendimento energético seja elevado, para que
percorra um maior numero de km com um menor
consumo de gasolina. Assim, procurou-se estudar um
carro OPEL e verificar o seu consumo de gasolina
consoante as suas velocidades (40-120km/h).
Será o carro eficiente segundo as
necessidades do seu utilizador?

7. Resultados Obtidos
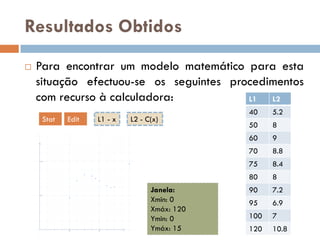
 Sabendo que o carro possui um consumo médio de
7,93 L/km, elaborou-se um estudo para determinar
o seu consumo em velocidades compreendidas entre
40 e 120 km/h:
x 40 50 60 70 75 80 90 95 100 120
C (x) 5,2 8 9 8,8 8,4 8 7,2 6,9 7 10,8
Tabela 1. Dados obtidos através do estudo feito.
Intervalo de variação da função:
- Positivo: x: ]0;120] y: ]0;+∞[
- Negativo: Não existe pois não pode haver consumo negativo.

8. Resultados Obtidos
 Para encontrar um modelo matemático para esta
situação efectuou-se os seguintes procedimentos
com recurso à calculadora: L1 L2
40 5.2
Stat Edit L1 - x L2 - C(x)
50 8
60 9
70 8.8
75 8.4
80 8
Janela: 90 7.2
Xmin: 0 95 6.9
Xmáx: 120
Ymin: 0 100 7
Ymáx: 15 120 10.8

9. Resultados Obtidos
Stat Calc CubicReg L1,L2,Y1
C(x)
Janela:
Xmin: 0
Xmáx: 120
Ymin: 0
Ymáx: 15
C(x):

10. Resultados Obtidos
 Estudo da função:
- Monotonia.
1. Encontrar a Derivada:
se C(x)= ,
então: C’(x)=
Janela:
Xmin: 0
Xmáx: 120
Ymin: 0
Ymáx: 15

11. Resultados Obtidos
2. Encontrar os zeros:
C’(x): C’(x)=0  
 x=63,4 V x=95,7
C(x): C(x)=0  
 x=30
3. Fazer o quadro de sinais:
x -∞ 0 30 63,4 95,7 120 +∞
C’(x) + + 0 - 0 +
C(x) 0 Máx Min

12. Resultados Obtidos
4. Encontrar o mínimo e o máximo:
Máximo:
C(63,4) =
= 9,2
Mínimo:
C(95,7) =
= 7,5

13. Resultados Obtidos
Estudo da Função: Máximo
x=62,6
y=9,2
x=120
y=10,8
Mínimo
x=95,7 Janela:
y=7,5 Xmin: 0
Xmáx: 120
Zero x=40 Ymin: 0
x=30 y=5,2 Ymáx: 15
y=0

14. Resultados Obtidos
 É possível ainda calcular os valores dos ângulos
compreendidos entre a tangente ao ponto e o eixo
Ox:
m = tgα
C’(x)

15. Resultados Obtidos
 Para x=40,
C’(40) = 
 C’(40) = 0,4
se:
m = tgα
então: 
 
 α
Situação para declive positivo.

16. Resultados Obtidos
 Para x=80,
C’(80) = 
 C’(80) = - 0,08
se: m = tgα
então:  Ω
α
 

Ω: 180 – 4,57=175,43º
Situação para declive negativo.

17. Resultados Obtidos
 Para x=62,6,
Como é um máximo, a sua derivada é igual a
0. Logo o ângulo é igual a 0. O mesmo aconteceria
para o mínimo (x=95,7).
α
α

18. Conclusão
 O carro, será mais eficiente caso o seu utilizador
ande regularmente a uma velocidade
compreendida entre os [63,4;95,7] km/h, mas
principalmente quando essa velocidade se
aproxima dos 95,7 km/h.

19. Elementos Consultados
 Costa, B.;Resende, L.; Rodrigues, E. (2010); “Espaço
11”; Matemática A; Editora: ASA