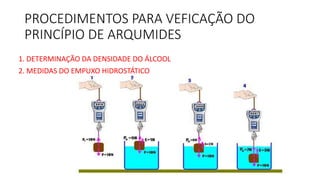
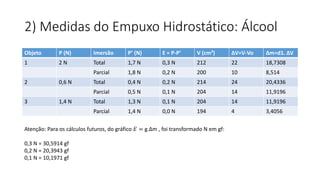
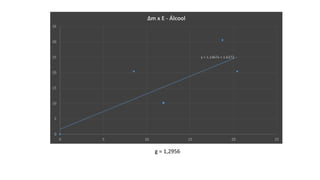
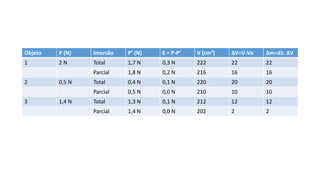
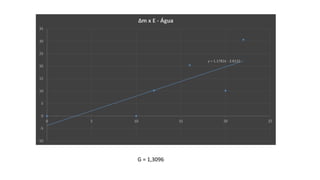
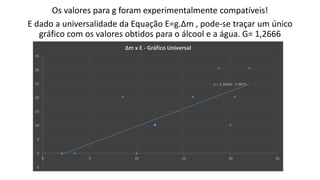
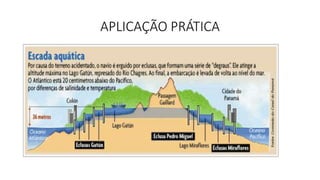
Este documento descreve experimentos realizados para verificar o Princípio de Arquimedes através da determinação da densidade do álcool e medição do empuxo hidrostático em objetos imersos no álcool e na água. Os resultados experimentais validaram a equação universal E=g.Δm para o empuxo.

1. Princípio de Arquimedes –
FÍSICA EXPERIMENTAL II
COMPPONENTES:
Fernanda Diniz
Kmilly Campos
Lucas Angra
Priscila

2. INTRODUÇÃO
• Quando imerso num fluido um corpo sofre,
em virtude do princípio de Pascal, pressões
diferenciadas sobre a sua superfície,
maiores na sua parte inferior que na sua
parte superior, levando a uma força
resultante vertical para cima.
• Este fenômeno é regido pelo chamado
princípio de Arquimedes, em homenagem
ao célebre pensador grego que o observou
já no século III a.C..

3. Experimento Princípio de Arquimedes
Arquimedes, um matemático, físico,
engenheiro grego, foi talvez o maior cientista da
Antiguidade. Não só descobriu a natureza do
empuxo, mas também calculou a razão entre a
circunferência de um círculo e o seu diâmetro e
demostrou também cálculos de volume e área de
superfícies geométricas.

4. Experimento Princípio de Arquimedes
O Princípio de Arquimedes
Um corpo total ou parcialmente imerso num fluido recebe do
fluido um empuxo igual e contrário ao peso da porção de fluido deslocado
e aplicado no centro de gravidade de massa. ( H. MOYSES NUSSENZVEIG,
Curso de física básica vol. 2, p. 11).

5. Experimento Principio de Arquimedes
Teoria
Σ 𝑓𝑦 =
0
𝐸 −
𝑃 = 0
𝐸 =
𝑚𝑔
1
Σ 𝐹𝑓𝑙𝑢𝑖𝑑𝑜 = 𝐵 = 𝐹𝑓𝑢𝑛𝑑𝑜 − 𝐹 𝑇𝑜𝑝𝑜
E − 𝑃 = 𝑚 𝐿. 𝑔 − 𝑀. 𝑔 = 𝜌 𝑓. 𝑉.g − 𝜌𝑐. 𝑉.g
E = 𝜌 𝑓. 𝑔 𝑉 E = 𝑚. 𝑔
𝐦 = 𝝆 𝒇 . 𝑽
𝐶𝑜𝑛𝑐𝑙𝑢í𝑚𝑜𝑠 𝑞𝑢𝑒 𝑚 é igual a massa do líquido deslocado e que o
Empuxo é igual ao peso do fluido deslocado.
E = 𝑃𝑓𝑢𝑛𝑑𝑜 . 𝐴 − 𝑃𝑇𝑜𝑝𝑜 . 𝐴 = Δ𝑃. 𝐴 = 𝜌 𝑓 . g. h. A
E − 𝑃 = 𝜌 𝑓− 𝜌 𝐶 𝑉. 𝑔3
𝐸
𝑃
2

6. Materiais comuns para verificação do
princípio de Arquimedes
• 1. mola
• 2. porta pesos
• 3. conjunto de massas aferidas
• 4. proveta graduada
• 5. béquer
• 6. balança
• 7. picnômetro
• 8. álcool
• 9. água
• 10. diferentes objetos

7. PROCEDIMENTOS PARA VEFICAÇÃO DO
PRINCÍPIO DE ARQUMIDES
1. DETERMINAÇÃO DA DENSIDADE DO ÁLCOOL
2. MEDIDAS DO EMPUXO HIDROSTÁTICO

8. Tratamento de Dados
Principio de Arquimedes

9. 1) Determinação da densidade do Álcool
𝑑𝑟𝑒𝑙 = (75,1 − 32,1)/(82,6 − 32,1)
𝑑𝑟𝑒𝑙 = 0,8514
𝑔
𝑐𝑚3
Como a densidade da água é 1g/cm³,
temos que a densidade do álcool é 0,8514g/cm³.

10. 2) Medidas do Empuxo Hidrostático: Álcool
Objeto P (N) Imersão P’ (N) E = P-P’ V (cm³) ∆V=V-Vo ∆m=d1. ∆V
1 2 N Total 1,7 N 0,3 N 212 22 18,7308
Parcial 1,8 N 0,2 N 200 10 8,514
2 0,6 N Total 0,4 N 0,2 N 214 24 20,4336
Parcial 0,5 N 0,1 N 204 14 11,9196
3 1,4 N Total 1,3 N 0,1 N 204 14 11,9196
Parcial 1,4 N 0,0 N 194 4 3,4056
Atenção: Para os cálculos futuros, do gráfico 𝐸 = g.∆m , foi transformado N em gf:
0,3 N = 30,5914 gf
0,2 N = 20,3943 gf
0,1 N = 10,1971 gf

11. y = 1.1467x + 1.6272
0
5
10
15
20
25
30
35
0 5 10 15 20 25
∆m x E - Álcool
g = 1,2956

12. Objeto P (N) Imersão P’ (N) E = P-P’ V (cm³) ∆V=V-Vo ∆m=d1. ∆V
1 2 N Total 1,7 N 0,3 N 222 22 22
Parcial 1,8 N 0,2 N 216 16 16
2 0,5 N Total 0,4 N 0,1 N 220 20 20
Parcial 0,5 N 0,0 N 210 10 10
3 1,4 N Total 1,3 N 0,1 N 212 12 12
Parcial 1,4 N 0,0 N 202 2 2

13. y = 1.1782x - 3.8132
-10
-5
0
5
10
15
20
25
30
35
0 5 10 15 20 25
∆m x E - Água
G = 1,3096

14. Os valores para g foram experimentalmente compatíveis!
E dado a universalidade da Equação E=g.∆m , pode-se traçar um único
gráfico com os valores obtidos para o álcool e a água. G= 1,2666
y = 1.2666x - 2.9673
-5
0
5
10
15
20
25
30
35
0 5 10 15 20 25
∆m x E - Gráfico Universal

15. APLICAÇÃO PRÁTICA

16. CONCLUSÃO
Princípio de Arquimedes que pode ser
dividida em duas partes:
• Todo corpo submerso em um líquido,
desloca desse líquido uma
quantidade determinada, cujo
volume é exatamente igual ao
volume do corpo submerso.
• O corpo submerso no líquido “perde”
de seu peso uma quantidade igual ao
peso do volume de líquido igual ao
volume submerso do corpo.

17. REFERÊNCIAS
• http://veja.abril.com.br/101199/p_072.html
• http://www.fis.ufba.br/dfg/fis2/Principio_Arquimedes.pdf
• http://www.infoescola.com/fisica/principio-de-arquimedes-empuxo/
• http://matematicaecidadania.wordpress.com/2011/11/03/biografia-
de-arquimedes/