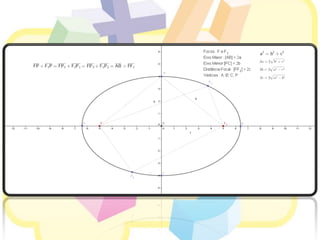
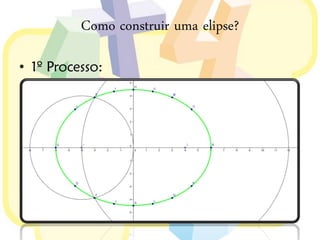
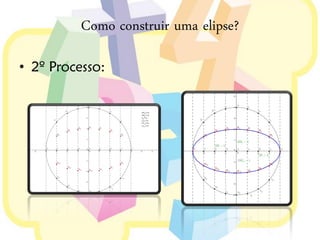
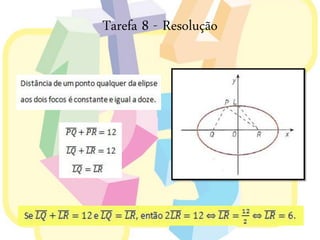
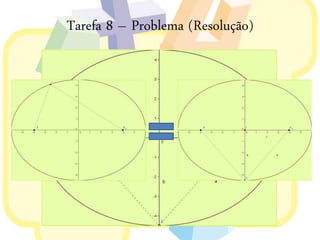
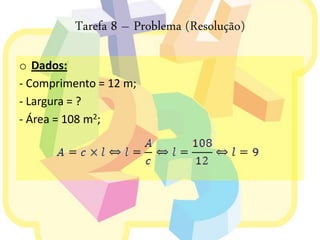
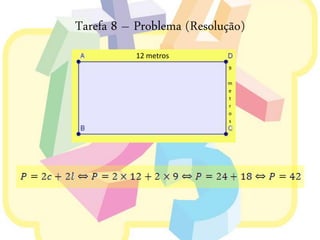
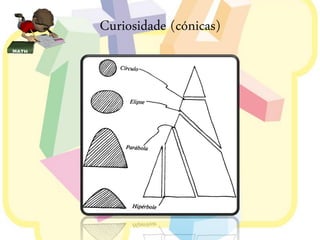
Este documento discute elipses geométricas. Explica que uma elipse é o conjunto de pontos cuja soma das distâncias aos dois focos é constante, apresenta três métodos para construir elipses, e mostra como derivar a equação de uma elipse a partir de uma circunferência. Resolve também um exercício e um problema sobre elipses.

1. Escola Secundária de Pinheiro e Rosa
Ano Lectivo: 2011/2012
10ºA
Alunos: Igor Albernaz e Lucas Sá
Professor: Luís Vilhena & Emila Santos

2. Introdução
• O que é uma elipse?
• Como construir uma elipse?
• Como chegar à equação da elipse?
• Resolução de um Exercício
• Resolução de um Problema

3. O que é uma elipse?
• Elipse é o lugar geométrico dos pontos do
plano tais que a soma das distâncias a dois
pontos fixos (focos) é constante e maior
que a distância entre os focos.

5. Como construir uma elipse?
• 1º Processo:

6. Como construir uma elipse?
• 2º Processo:

7. Como construir uma elipse?
• 3º Processo:
http://www.youtube.com/watch?v=7UD8hOs-vaI&feature=player_embedded

8. Como chegar à equação da elipse?
• Circunferência de centro C(0;0) e
raio 4.
• Equação da circunferência é:
• Considera-se um ponto da
circunferência, P(x;y) e um ponto da
elipse P’(x1;y1).
• x=x1 e y=2y1

9. • 16 é o quadrado de 4, e 4 é o semieixo maior da elipse, a.
• 4 é o quadrado de 2, e 2 é o semieixo menor da elipse, b.
Caso o eixo maior
da elipse pertença
ao eixo das abcissas.
Caso o eixo maior da
elipse pertença ao
eixo das ordenadas.

10. Tarefa 8 - Exercício

11. Tarefa 8 - Resolução

12. Tarefa 8 – Exercício (Resolução)

13. Tarefa 8 - Problema

14. Tarefa 8 – Problema (Resolução)

15. Tarefa 8 – Problema (Resolução)
• Pretende-se saber o perímetro do rectângulo.
• Sabe-se que:
– A corda do jardineiro tem 12 metros, ou seja,
– O eixo maior da elipse é igual ao comprimento do
rectângulo;
– O eixo menor da elipse é igual à largura do rectângulo;
– A área do rectângulo é 108 m2;

16. Tarefa 8 – Problema (Resolução)
o Dados:
- Comprimento = 12 m;
- Largura = ?
- Área = 108 m2;

17. Tarefa 8 – Problema (Resolução)
12 metros
9
m
e
t
r
o
s

18. Tarefa 8 – Problema (Resolução)
• Será que tem rede suficiente para a vedação?
Estuda o problema e indica o comprimento mínimo
de rede necessário para proteger o canteiro.
• R.: Podemos assim concluir que os 40 metros de rede que o
jardineiro possui não são suficientes para vedar o canteiro, e
que são necessários no mínimo 42 metros para o fazer.

19. Curiosidade (cónicas)