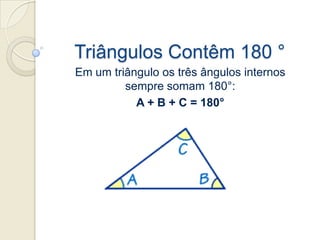
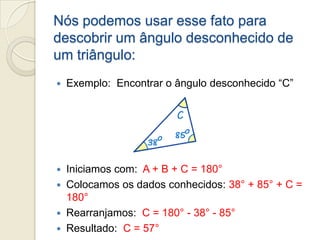
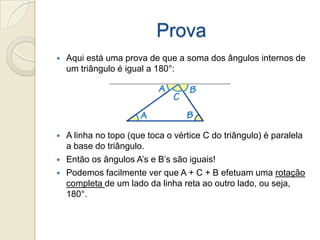
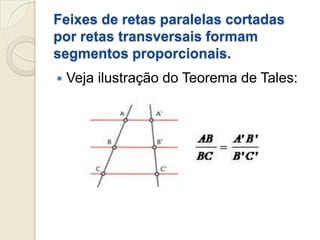
1) A soma dos ângulos internos de um triângulo é igual a 180 graus. 2) Isso pode ser usado para calcular um ângulo desconhecido, dado os outros dois ângulos. 3) Tales provou geometricamente que a soma dos ângulos internos é 180° usando a propriedade de que linhas paralelas cortadas por uma transversal formam ângulos correspondentes.

1. Triângulos Contêm 180 °Em um triânguloostrêsângulosinternossempresomam180°: A + B + C = 180°

2. Nós podemos usar esse fato para descobrir um ângulo desconhecido de um triângulo:Exemplo: Encontrar o ângulo desconhecido “C”Iniciamos com: A + B + C = 180°Colocamos os dados conhecidos: 38° + 85° + C = 180°Rearranjamos: C = 180° - 38° - 85°Resultado: C = 57°

3. ProvaAqui está uma prova de que a soma dos ângulos internos de um triângulo é igual a 180°:A linha no topo (que toca o vértice C do triângulo) é paralela a base do triângulo.Então os ângulos A’s e B’s são iguais!Podemos facilmente ver que A + C + B efetuam uma rotação completa de um lado da linha reta ao outro lado, ou seja, 180°.

4. Teorema de TalesTales nasceu na cidade de Mileto, colônia grega localizada na Ásia menor. Filósofo, Matemático, Astrônomo, desenvolveu uma teoria que ficou conhecida como: Teorema de Tales.Tales ficou conhecido por ter medido a altura de uma pirâmide com base no comprimento de sua sombra. Ele concluiu que os raios solares chegam à Terra inclinados, partindo dessa afirmação ele conseguiu medir a altura da pirâmide da seguinte forma: Fincou uma estaca ao lado da pirâmide e observou que no instante em que o comprimento da sombra da estaca era igual à medida do comprimento da estaca, a altura da pirâmide teria o mesmo comprimento da sua sombra.

5. Feixes de retas paralelas cortadas por retas transversais formam segmentos proporcionais.Veja ilustração do Teorema de Tales:

6. Exemplo 1Calcule o valor de x na ilustração abaixo:4x = 15x = 15/4x = 3,75

7. Exemplo 2Aplique o Teorema de Tales e calcule o valor de x.6(2x-3) = 5(x+2)12x – 18 = 5x + 102x – 5x = 10 + 187x = 28x = 28/7x = 4