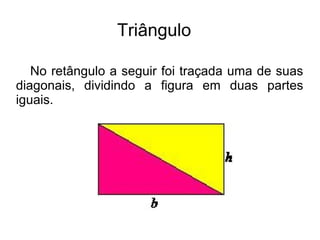
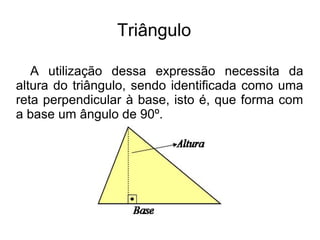
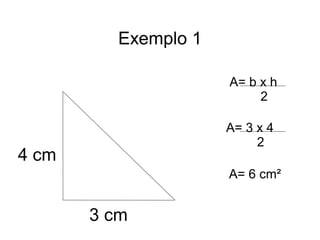
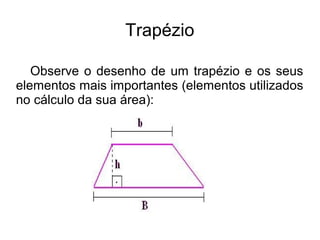
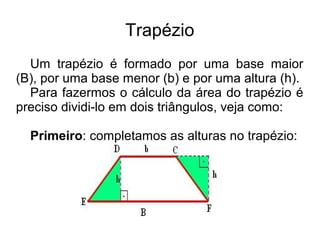
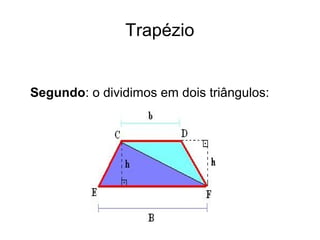
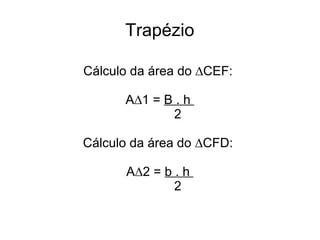
O documento apresenta os métodos para calcular a área de triângulos e trapézios utilizando fórmulas matemáticas. Para triângulos, a área é igual à metade da base vezes a altura. Para trapézios, ele é dividido em dois triângulos e a área total é a soma das áreas desses triângulos, que é igual à metade da soma das bases vezes a altura.

1. Trabalho de Geometria
Escola: Caldas Júnior
Nomes: Júlia e Joana
Turma: 8° Ano B
Disciplina: Matemática
Professora: Loici Pontalti

2. Área do Triângulo
Nos estudos relacionados à Geometria, o
triângulo é considerado uma das figuras mais
importantes em razão da sua imensa utilidade no
cotidiano. Com o auxílio de um retângulo e suas
propriedades, demonstraremos como calcular a
área de um triângulo.

3. Triângulo
No retângulo a seguir foi traçada uma de suas
diagonais, dividindo a figura em duas partes
iguais.

4. Triângulo
Note que a área total do retângulo é dada pela
expressão A = b x h. Considerando que a diagonal
dividiu o retângulo em duas partes iguais formando
dois triângulos, a área de cada triângulo será igual
à metade da área total do retângulo, constituindo
na seguinte expressão matemática:
A= b x h
2

5. Triângulo
A utilização dessa expressão necessita da
altura do triângulo, sendo identificada como uma
reta perpendicular à base, isto é, que forma com
a base um ângulo de 90º.

6. Exemplo 1
3 cm
4 cm
A= b x h
2
A= 3 x 4
2
A= 6 cm²

7. Área do Trapézio
Na geometria, o trapézio é um quadrilátero
com dois lados paralelos, chamados de base
maior e base menor.

8. Trapézio
A área do trapézio está relacionada com a área
do triângulo que é calculada utilizando a seguinte
fórmula: A = b . h (b = base e h =
2
altura).

9. Trapézio
Observe o desenho de um trapézio e os seus
elementos mais importantes (elementos utilizados
no cálculo da sua área):

10. Trapézio
Um trapézio é formado por uma base maior
(B), por uma base menor (b) e por uma altura (h).
Para fazermos o cálculo da área do trapézio é
preciso dividi-lo em dois triângulos, veja como:
Primeiro: completamos as alturas no trapézio:

11. Trapézio
Segundo: o dividimos em dois triângulos:

12. Trapézio
A área desse trapézio pode ser calculada
somando as áreas dos dois triângulos (∆CFD e
∆CEF). (∆ este símbolo quer dizer triângulo).
Antes de fazer o cálculo da área de cada
triângulo separadamente observamos que eles
possuem bases diferentes e alturas iguais.

13. Trapézio
Cálculo da área do ∆CEF:
A∆1 = B . h
2
Cálculo da área do ∆CFD:
A∆2 = b . h
2

14. Trapézio
Somando as duas áreas encontradas, teremos o cálculo
da área de um trapézio qualquer:
AT = A∆1 + A∆2
AT = B . h + b . h
2 2
(colocar a altura (h) em evidência, pois é um termo comum aos dois
fatores)
AT = (B + b) . h
2

15. Trapézio
Portanto, no cálculo da área de um trapézio
qualquer utilizamos a seguinte fórmula:
A = (B + b) . h
2
h = altura
B = base maior do trapézio
b = base menor do trapézio