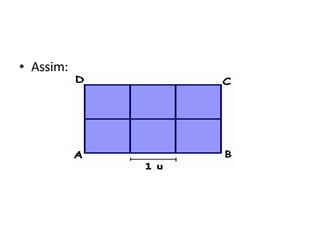
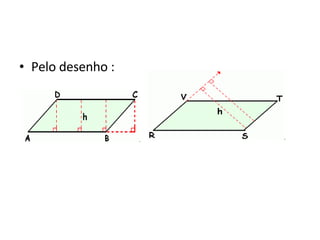
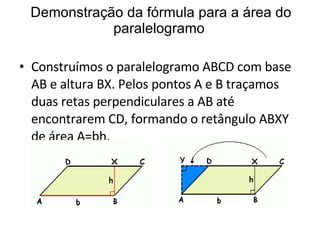
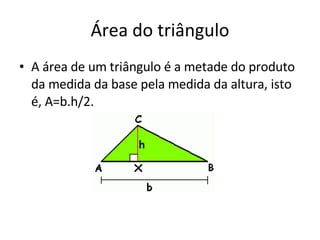
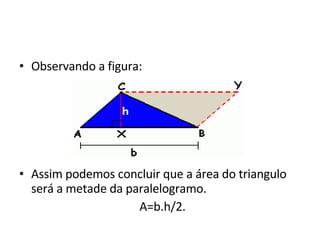
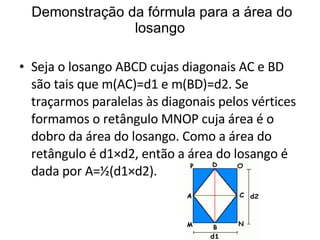
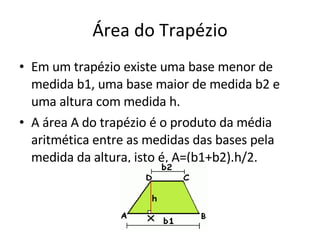
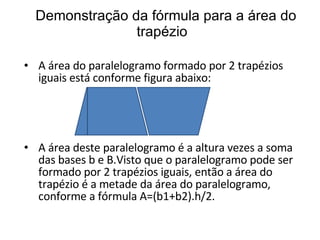
O documento apresenta as fórmulas para calcular a área de diferentes figuras planas (retângulo, quadrado, paralelogramo, triângulo, losango e trapézio) e demonstra como derivá-las geometricamente. Explica que a área é medida em unidades quadradas e define a unidade de área com base em um quadrado de lado unitário. Fornece as seguintes fórmulas: área do retângulo é a base vezes a altura; área do quadrado é o lado ao quadrado; área do paralelogramo, tri

1. Áreas de polígonos Demonstrações de suas fórmulas

2. Antes mesmo de falarmos em áreas devemos saber qual sua unidade de medida,não acha? Unidade de área Para a unidade de medida de área, traçamos um quadrado cujo lado tem uma unidade de comprimento. Esta unidade pode ser o metro, o centímetro, o quilômetro, etc.

3. Área do Retângulo A figura abaixo mostra o retângulo ABCD, que mede 3 unidades de comprimento e 2 unidades de altura. O segmento horizontal que passa no meio do retângulo e os segmentos verticais, dividem o retângulo em seis quadrados tendo cada um 1 unidade de área.

4. Assim:

5. A área do retângulo ABCD é a soma das áreas destes seis quadrados. O número de unidades de área do retângulo coincide com o obtido pelo produto do número de unidades do comprimento da base AB pelo número de unidades da altura BC. O lado do retângulo pode ser visto como a base e o lado adjacente como a altura, assim, a área A do retângulo é o produto da medida da base b pela medida da altura h.

6. Área do Quadrado Um quadrado é um caso particular de retângulo cuja medida da base é igual à medida da altura. A área do quadrado pode ser obtida pelo produto da medida da base por si mesma. Esta é a razão pela qual a segunda potência do número x, indicada por x², tem o nome de quadrado de x e a área A do quadrado é obtida pelo quadrado da medida do lado x. Sendo então : A = x²

7. Área do Paralelogramo Qualquer lado do paralelogramo pode ser tomado como sua base e a altura correspondente é o segmento perpendicular à reta que contém a base até o ponto onde esta reta intercepta o lado oposto do paralelogramo. No paralelogramo ABCD, os segmentos verticais tracejados são congruentes e qualquer um deles pode representar a altura do paralelogramo em relação à base AB.

8. No paralelogramo RSTV, os dois segmentos tracejados são congruentes e qualquer um deles pode representar a altura do paralelogramo em relação à base RV. A área A do paralelogramo é obtida pelo produto da medida da base b pela medida da altura h, isto é, A=b×h.

9. Pelo desenho :

10. Demonstração da fórmula para a área do paralelogramo Construímos o paralelogramo ABCD com base AB e altura BX. Pelos pontos A e B traçamos duas retas perpendiculares a AB até encontrarem CD, formando o retângulo ABXY de área A=bh.

11. Os triângulos ADY e BCX são congruentes, pois são triângulos retângulos, possuem hipotenusas congruentes, pois são lados opostos de um paralelogramo (AD e BC) e um dos catetos congruentes pois (AY=BX) por serem paralelas compreendidas entre paralelas. Portanto, a área do retângulo ABXY é b.h e é igual à área do paralelogramo ABCD.

12. Área do triângulo A área de um triângulo é a metade do produto da medida da base pela medida da altura, isto é, A=b.h/2.

13. Demonstração da fórmula para a área do triângulo Construímos o triângulo ABC com base AB e altura XC. Traçamos uma reta paralela ao segmento AB que passa pelo ponto C e uma reta paralela ao segmento AC que passa pelo ponto B e dessa forma construímos o paralelogramo ABYC cuja área é o dobro da área do triângulo ABC.

14. Observando a figura: Assim podemos concluir que a área do triangulo será a metade da paralelogramo. A=b.h/2.

15. Área do losango O losango é um paralelogramo e a sua área é também igual ao produto do comprimento da medida da base pela medida da altura. A área do losango é o semi-produto das medidas das diagonais, isto é, A=(d 1 ×d 2 )/2.

16. Demonstração da fórmula para a área do losango Seja o losango ABCD cujas diagonais AC e BD são tais que m(AC)=d1 e m(BD)=d2. Se traçarmos paralelas às diagonais pelos vértices formamos o retângulo MNOP cuja área é o dobro da área do losango. Como a área do retângulo é d1×d2, então a área do losango é dada por A=½(d1×d2).

17. Área do Trapézio Em um trapézio existe uma base menor de medida b1, uma base maior de medida b2 e uma altura com medida h. A área A do trapézio é o produto da média aritmética entre as medidas das bases pela medida da altura, isto é, A=(b1+b2).h/2.

18. Demonstração da fórmula para a área do trapézio A área do paralelogramo formado por 2 trapézios iguais está conforme figura abaixo: A área deste paralelogramo é a altura vezes a soma das bases b e B.Visto que o paralelogramo pode ser formado por 2 trapézios iguais, então a área do trapézio é a metade da área do paralelogramo, conforme a fórmula A=(b1+b2).h/2.