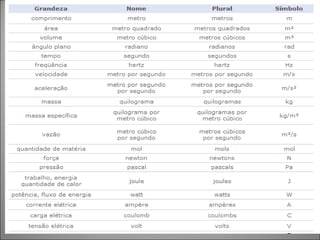
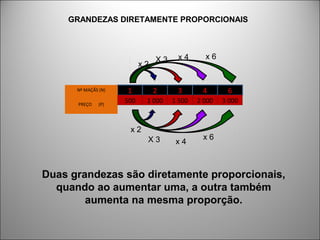
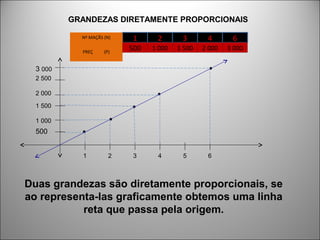
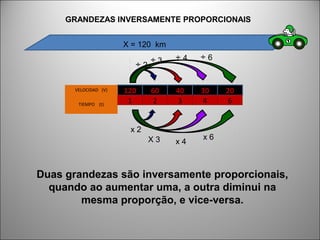
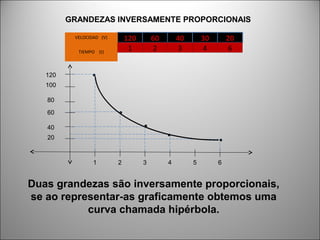
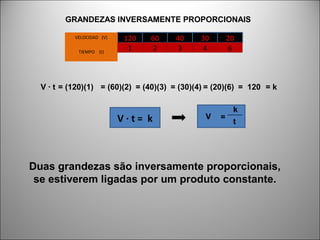
O documento discute o conceito de grandezas e suas proporcionalidades. Grandezas podem ser diretamente proporcionais, quando aumentam na mesma proporção, ou inversamente proporcionais, quando uma aumenta e a outra diminui na mesma proporção. Exemplos e equações mostram como identificar cada tipo de proporcionalidade entre grandezas.

1. Grandezas

3. Grandeza
É uma relação numérica estabelecida com um
objeto. Assim, a altura de uma árvore, o
volume de um tanque, o peso de um corpo, a
quantidade pães, entre outros, são grandezas.
Grandeza é tudo que você pode contar,
medir, pesar, enfim, enumerar.

5. 1 2 3 4 6Nº MAÇÃS (N)
PREÇO (P)
500 1 000 1 500 2 000 3 000
GRANDEZAS DIRETAMENTE PROPORCIONAIS
Duas grandezas são diretamente proporcionais,
quando ao aumentar uma, a outra também
aumenta na mesma proporção.
x 2
X 3 x 4 x 6
x 2
X 3 x 4
x 6

6. 1 2 3 4 6Nº MAÇÃS (N)
PREÇ (P)
500 1 000 1 500 2 000 3 000
500
3 000
2 500
1 000
1 500
2 000
1 65432
Duas grandezas são diretamente proporcionais, se
ao representa-las graficamente obtemos uma linha
reta que passa pela origem.
GRANDEZAS DIRETAMENTE PROPORCIONAIS

7. 1 2 3 4 6Nº MAÇÃS (N)
PREÇO (P)
500 1 000 1 500 2 000 3 000
P
N
=
500
1
=
1 000
2
=
1 500
3
=
2 000
4
=
3 000
6
= 500 = k
P
N
= k P = k N
Duas grandezas são diretamente
proporcionais, se estão ligadas por um
quociente constante.
GRANDEZAS DIRETAMENTE PROPORCIONAIS

8. 120 60 40 30 20VELOCIDAD (V)
TIEMPO (t)
1 2 3 4 6
Duas grandezas são inversamente proporcionais,
quando ao aumentar uma, a outra diminui na
mesma proporção, e vice-versa.
÷ 2
÷ 3 ÷ 4 ÷ 6
x 2
X 3 x 4
x 6
X = 120 km
GRANDEZAS INVERSAMENTE PROPORCIONAIS

9. 20
120
100
40
60
80
1 65432
Duas grandezas são inversamente proporcionais,
se ao representar-as graficamente obtemos uma
curva chamada hipérbola.
120 60 40 30 20VELOCIDAD (V)
TIEMPO (t)
1 2 3 4 6
GRANDEZAS INVERSAMENTE PROPORCIONAIS

10. = k
k
t
=VV · t = k
Duas grandezas são inversamente proporcionais,
se estiverem ligadas por um produto constante.
120 60 40 30 20VELOCIDAD (V)
TIEMPO (t)
1 2 3 4 6
V · t = (120)(1) = (60)(2) = (40)(3) = (30)(4) = (20)(6) = 120
GRANDEZAS INVERSAMENTE PROPORCIONAIS

11. Grandezas
diretamente
proporcionais
Grandezas
inversamente
proporcionais
k
Q
P
= kQP =⋅

12. Compondo Proporções
Trabalhamos com proporções fixas, que
simplesmente ditavam que uma fração deveria
permanecer constante. Mas o que acontece se
uma grandeza é proporcional a várias grandezas
ao mesmo tempo?

13. Podemos trabalhar cada proporcionalidade
individualmente, mas há um método para resolvê-las
com uma única equação.
Começaremos com o clássico problema:
Sr. José precisava consertar
uma cerca quebrada
em sua fazenda.
Pesquisa google(23/06/2008)
501 x 375 - 68k - jpgbloglog.globo.com

14. Como a boiada voltaria das pastagens novas em
uma semana, precisava decidir quantos
trabalhadores contratar para terminar a cerca a
tempo.
Na construção original da cerca, ele empregou 24
homens que ergueram os 100 metros de cerca
em duas semanas.
Sabendo que o buraco se extende por apenas
25 metros, quantos homens serão
nescessários?

15. • O número de homens é inversamente proporcional ao
tempo
• O tamanho da cerca é diretamente proporcional ao
tempo
• O tamanho da cerca é diretamente proporcional ao
número de homens
• Para facilitar o trabalho, escrevemos uma tabela:
Homens Tempo Tamanho
24 2 semanas 100m
X 1 semana 25m

16. Exercícios
1) Em cada um dos casos abaixo, verifique se há ou não
proporcionalidade. Se existir, expresse tal fato algebricamente,
indicando o valor da constante de proporcionalidade.
a) A altura a de uma pessoa é diretamente proporcional a sua idade t?
b) A massa m de uma pessoa é diretamente proporcional a sua idade t?
c) O perímetro p de um quadrado é diretamente proporcional a seu lado a?
d) A diagonal d de um quadrado é diretamente proporcional ao seu lado a?
e) O comprimento c de uma circunferência é diretamente proporcional a seu
diâmetro d?

17. 2) Um prêmio P da loteria deve ser dividido em partes iguais,
cabendo um valor x a cada um dos n ganhadores. Considere
P = 400.000 reais e preencha a tabela abaixo.
n 1 2 3 4 5 8 10 20
x
3) A tabela abaixo relaciona os valores de três grandezas x, y, e z,
que variam de modo inter-relacionado.
x 1 3 4 5 10 15 40 50 60 75 120 150
y 7 21 28 35 70 105 280 350 420 525 840 1050
z 300 100 75 60 30 20 7,5 6 5 4 2,5 2
Verifique se os diversos pares de grandezas ( x e y, x e z, y e z) são
direta ou inversamente proporcionais. Justifique sua resposta.