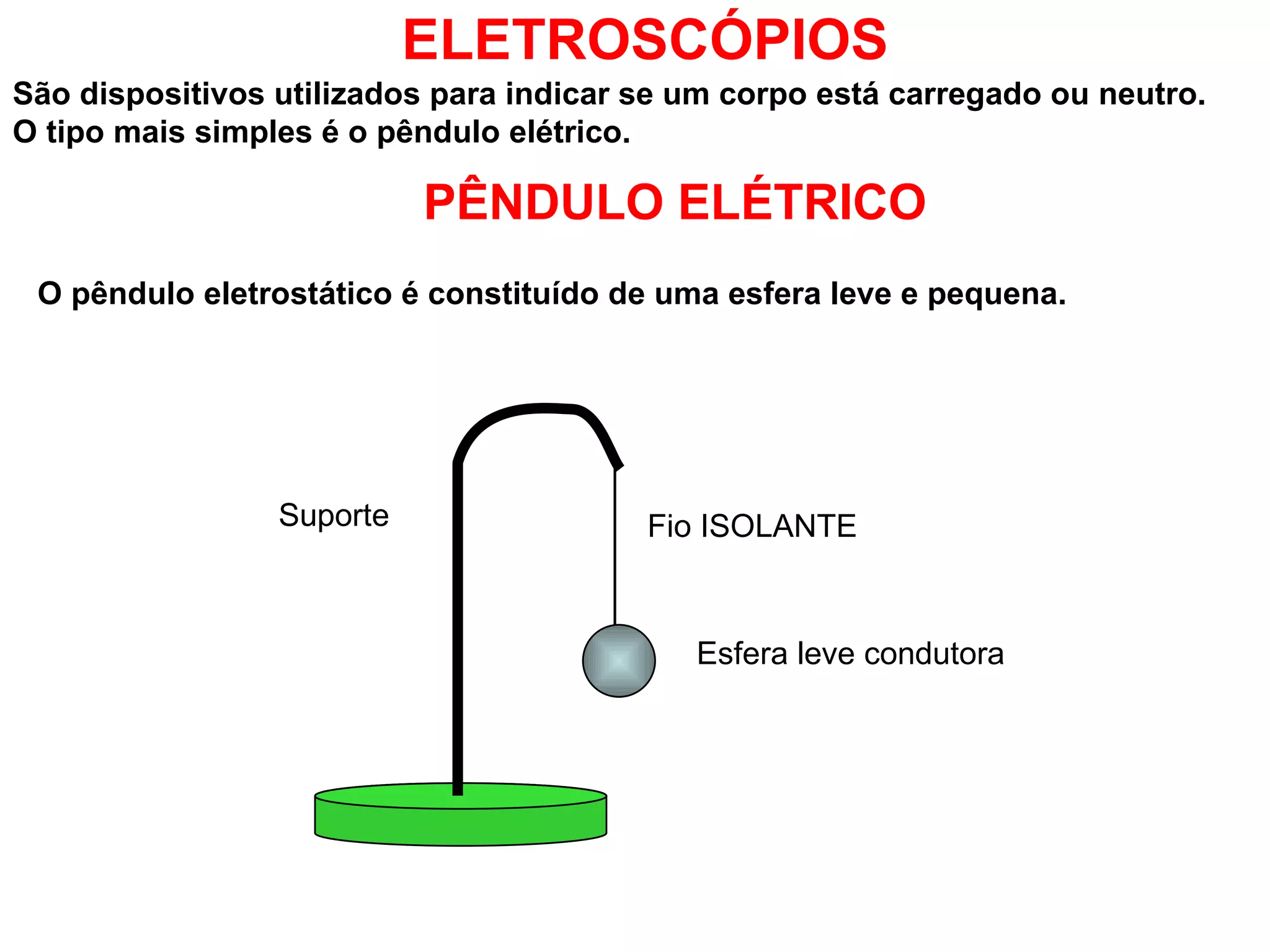
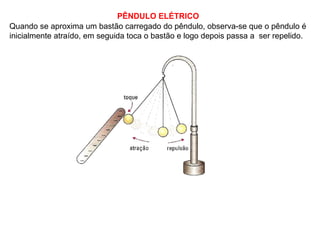
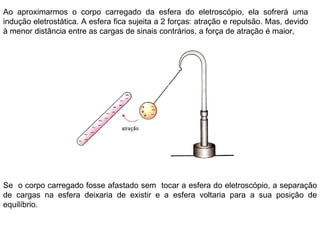
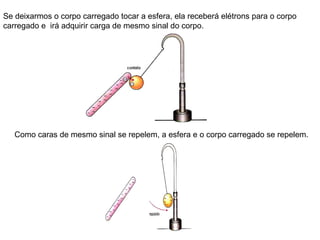
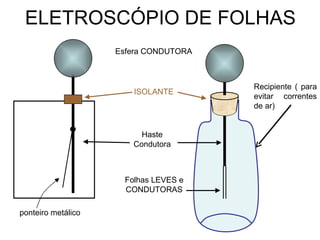
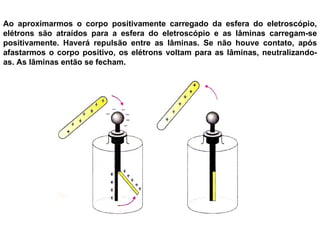
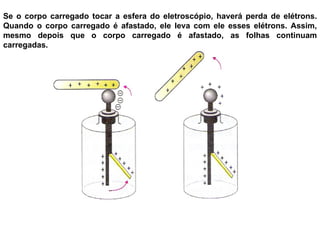
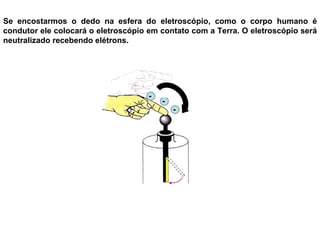
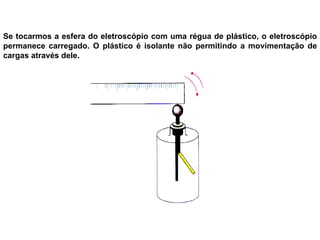
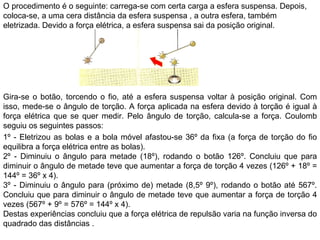
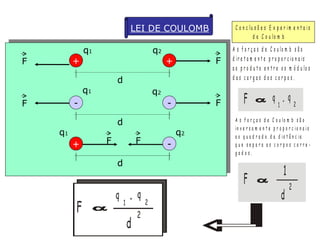
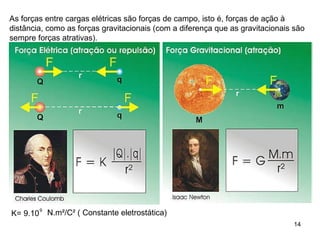
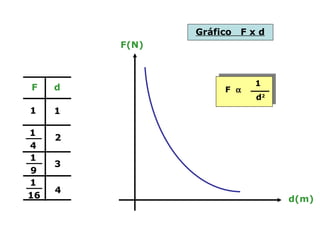
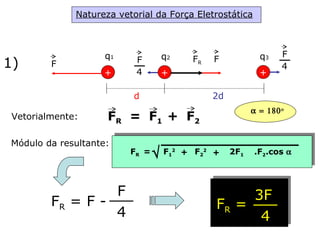
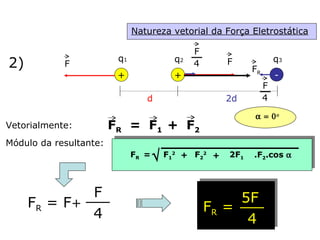
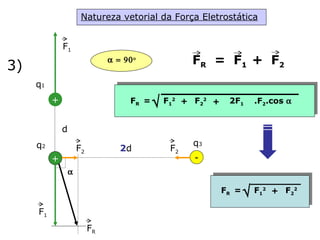
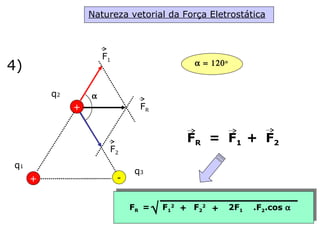
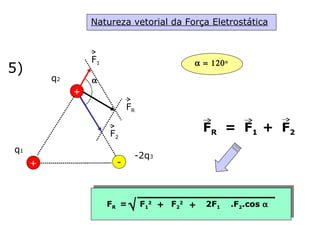
O documento descreve pêndulos elétricos e eletroscópios, que são dispositivos usados para indicar se um corpo está carregado ou não. Pêndulos elétricos usam uma esfera leve que é atraída ou repelida por corpos carregados, enquanto eletroscópios separam folhas condutoras quando carregados. O documento também explica a balança de torção de Coulomb, que mediu precisamente a força entre cargas elétricas variando com o inverso do quadrado da distância.

1. PÊNDULO ELÉTRICO ELETROSCÓPIOS São dispositivos utilizados para indicar se um corpo está carregado ou neutro. O tipo mais simples é o pêndulo elétrico. O pêndulo eletrostático é constituído de uma esfera leve e pequena. Esfera leve condutora Fio ISOLANTE Suporte

2. PÊNDULO ELÉTRICO Quando se aproxima um bastão carregado do pêndulo, observa-se que o pêndulo é inicialmente atraído, em seguida toca o bastão e logo depois passa a ser repelido.

3. Ao aproximarmos o corpo carregado da esfera do eletroscópio, ela sofrerá uma indução eletrostática. A esfera fica sujeita a 2 forças: atração e repulsão. Mas, devido à menor distância entre as cargas de sinais contrários, a força de atração é maior, Se o corpo carregado fosse afastado sem tocar a esfera do eletroscópio, a separação de cargas na esfera deixaria de existir e a esfera voltaria para a sua posição de equilíbrio.

4. Se deixarmos o corpo carregado tocar a esfera, ela receberá elétrons para o corpo carregado e irá adquirir carga de mesmo sinal do corpo. Como caras de mesmo sinal se repelem, a esfera e o corpo carregado se repelem.

5. ELETROSCÓPIO DE FOLHAS Esfera CONDUTORA Recipiente ( para evitar correntes de ar) Haste Condutora Folhas LEVES e CONDUTORAS ISOLANTE ponteiro metálico

6. Ao aproximarmos o corpo positivamente carregado da esfera do eletroscópio, elétrons são atraídos para a esfera do eletroscópio e as lâminas carregam-se positivamente. Haverá repulsão entre as lâminas. Se não houve contato, após afastarmos o corpo positivo, os elétrons voltam para as lâminas, neutralizando-as. As lâminas então se fecham.

7. Se o corpo carregado tocar a esfera do eletroscópio, haverá perda de elétrons. Quando o corpo carregado é afastado, ele leva com ele esses elétrons. Assim, mesmo depois que o corpo carregado é afastado, as folhas continuam carregadas.

8. Se encostarmos o dedo na esfera do eletroscópio, como o corpo humano é condutor ele colocará o eletroscópio em contato com a Terra. O eletroscópio será neutralizado recebendo elétrons. - - -

9. Se tocarmos a esfera do eletroscópio com uma régua de plástico, o eletroscópio permanece carregado. O plástico é isolante não permitindo a movimentação de cargas através dele.

11. Para medir as forças, Coulomb aperfeiçoou o método de detectar a força elétrica entre duas cargas por meio da torção de um fio. A partir dessa idéia criou um medidor de força extremamente sensível, denominado balança de torção . Charles A. Coulomb (1738 - 1806)

12. O procedimento é o seguinte: carrega-se com certa carga a esfera suspensa. Depois, coloca-se, a uma cera distância da esfera suspensa , a outra esfera, também eletrizada. Devido a força elétrica, a esfera suspensa sai da posição original. Gira-se o botão, torcendo o fio, até a esfera suspensa voltar à posição original. Com isso, mede-se o ângulo de torção. A força aplicada na esfera devido à torção é igual à força elétrica que se quer medir. Pelo ângulo de torção, calcula-se a força. Coulomb seguiu os seguintes passos: 1º - Eletrizou as bolas e a bola móvel afastou-se 36º da fixa (a força de torção do fio equilibra a força elétrica entre as bolas). 2º - Diminuiu o ângulo para metade (18º), rodando o botão 126º. Concluiu que para diminuir o ângulo de metade teve que aumentar a força de torção 4 vezes (126º + 18º = 144º = 36º x 4). 3º - Diminuiu o ângulo para (próximo de) metade (8,5º 9º), rodando o botão até 567º. Concluiu que para diminuir o ângulo de metade teve que aumentar a força de torção 4 vezes (567º + 9º = 576º = 144º x 4). Destas experiências concluiu que a força elétrica de repulsão varia na função inversa do quadrado das distâncias .

13. F F F F F F LEI DE COULOMB + + d q 1 q 2 - - d q 1 q 2 + - d q 1 q 2

14. As forças entre cargas elétricas são forças de campo, isto é, forças de ação à distância, como as forças gravitacionais (com a diferença que as gravitacionais são sempre forças atrativas). K= 9.10 9 N.m²/C² ( Constante eletrostática)

15. 1 2 3 4 1 Gráfico F x d 1 4 1 9 1 16 F d F(N) d(m) F   1 d 2

16. Módulo da resultante: 1) Vetorialmente:   Natureza vetorial da Força Eletrostática + + d q 1 q 2 + q 3 2d F F 4 F R F R = F - F 4 F R = 3F 4 F F 4 + F R = F 1 2 F 2 2 + 2F 1 .F 2 .cos   F R = F 1 F 2 +

17. Módulo da resultante: 2) Vetorialmente:   Natureza vetorial da Força Eletrostática + + d q 1 q 2 - q 3 2d F F R = F + F 4 F R = 5F 4 F R F 4 F F 4 F R = F 1 F 2 + + F R = F 1 2 F 2 2 + 2F 1 .F 2 .cos  

18. 3)    + q 2 q 1 - + q 3 d 2 d F 1 F 1 F 2 F 2 F R Natureza vetorial da Força Eletrostática F R = F 1 F 2 + + F R = F 1 2 F 2 2 + 2F 1 .F 2 .cos   + F R = F 1 2 F 2 2 

19. 4)    Natureza vetorial da Força Eletrostática + q 1 q 2 - + q 3 F 1 F 2 F R F R = F 1 F 2 + + F R = F 1 2 F 2 2 + 2F 1 .F 2 .cos  

20. 5)    Natureza vetorial da Força Eletrostática + q 1 q 2 - + -2q 3 F 1 F 2 F R F R = F 1 F 2 + + F R = F 1 2 F 2 2 + 2F 1 .F 2 .cos  