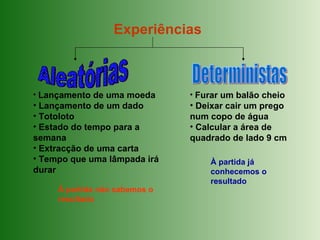
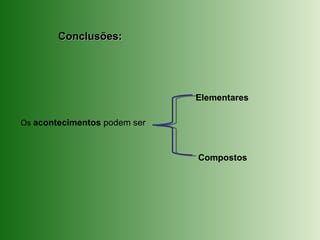
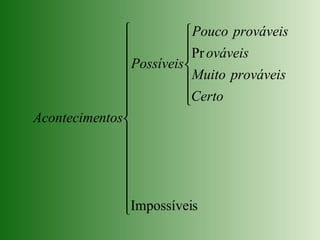
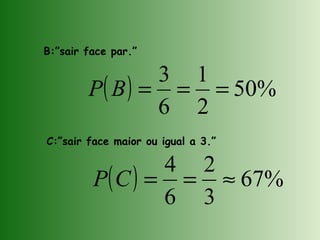Este documento introduz os conceitos fundamentais da teoria das probabilidades, como: eventos aleatórios versus deterministas, espaço amostral, eventos possíveis, cálculo de probabilidades usando a lei de Laplace. A teoria das probabilidades surgiu no século XVII a partir de problemas relacionados a jogos de azar, mas hoje tem aplicações em diversas áreas como economia, medicina e física.

1. Introdução à Teoria das
Probabilidades

2. No nosso dia-a-dia é frequente ouvirmos e dizermos expressões
tais como “improvável”, “por sorte” ou “por acaso” que deixam bem
claro que, em muitos acontecimentos das nossas vidas, não nos é
possível saber, antecipadamente, qual o seu desfecho.
Incapazes de controlar o acaso, conseguimos, contudo,
ter a noção da probabilidade de uma situação ocorrer ou não:
embora nunca possamos com segurança dizer “Amanhã vai
chover”, sabemos que a probabilidade de isso acontecer é maior no
Inverno do que no Verão;
é certo que ouviremos falar Inglês se formos a Inglaterra,
enquanto que em Portugal isso será improvável, mas não impossível;
é mais provável encontrar um atleta num ginásio do que numa
discoteca.

3. A imprevisibilidade aparece, irremediavelmente, associada aos chamados
“jogos de azar”:
ao lançar um dado, com as faces numeradas de 1 a 6, não sabemos
qual ficará voltada para cima;
ao tirarmos uma carta de um baralho não sabemos qual delas nos sairá;
não nos é possível saber previamente quais os números sorteados no
totoloto ou na lotaria (com grande pena nossa!).

4. Blaise Pascal
Matemático Francês
(1623-1662)
Foi exactamente a partir dos “jogos de azar” que no século XVII surge um ramo
da Matemática, que mais tarde se viria a chamar a Teoria das ProbabilidadesTeoria das Probabilidades.
Pierre Fermat
Matemático Francês
(1601-1665)
Segundo historiadores, o Cavaleiro De Méré,
conhecido por ser um jogador inveterado,
colocou algumas dúvidas sobre jogos a dois
matemáticos, Blaise Pascal e Pierre Fermat.
Estes, na tentativa de dar uma resposta ao
jogador, debruçaram-se sobre o assunto,
sendo, desta forma, dado o primeiro passo
para o nascimento desta teoria.
As probabilidades surgem, assim, como forma de quantificar
o grau de incerteza de um determinado acontecimento.

5. Embora o seu nascimento esteja ligado ao jogo, as Probabilidades têm, nos
nossos dias, aplicações em muitas outras ciências, nomeadamente, na
Economia, na Psicologia, na Medicina e até na Física e na Química. Uma área
onde a Teoria das Probabilidades é muito utilizada é a dos seguros. Hoje,
quando fazemos um contrato com uma companhia de seguros (seja esse
contrato um seguro de vida, um seguro de incêndios, um seguro automóvel ou
qualquer outro), o “prémio” a pagar à companhia foi determinado em função da
maior ou menor probabilidade de se verificar um acidente. Por exemplo, num
seguro automóvel, o “prémio” que se paga:
 é mais caro para carros com mais de 5 anos, já que a probabilidade
de se ter um desastre com um carro já com algum desgaste é maior do que com
um carro novo;
é mais caro se o condutor tiver carta de condução há menos de dois anos (a sua
inexperiência torna maior a probabilidade do acidente).
Há até companhias de seguros que fazem descontos para as mulheres condutoras!...

6. EXPERIÊNCIAS ALEATÓRIAS E DETERMINISTAS
Consideremos as seguintes experiências:
1.ª- “Deitar uma moeda num copo com água e verificar o que acontece.”
2.ª- “Lançar uma moeda ao ar e verificar se sai cara ou coroa.”
3.ª- “Tirar duas cartas à sorte de um baralho de 40 que foi
previamente baralhado.”
4.ª- “Deixar de regar um feijoeiro e verificar o que acontece.”
Será que em todas estas experiências conseguimos prever o resultado?
No caso da 1.ª experiência e da 4.ª, sabe-se à partida que a moeda
afunda-se e que a planta morre, caso não seja regada. Assim é possível
prever o resultado antes de realizarmos as experiências.
No caso da 2.ª e 3.ª experiências, não conseguimos prever o resultado,
para saber o que vai acontecer, tem-se mesmo, que realizar as experiências.

7. Experiências deterministas ou causaisExperiências deterministas ou causais – são todas as experiências
em que é possível saber o resultado final, antes de as realizarmos.
Só têm um resultado possível.
Experiências aleatórias ou casuaisExperiências aleatórias ou casuais – são todas as experiências em
que não é possível saber qual o resultado final, antes de as realizarmos.
Podem dar lugar a vários resultados.
Conclusão:Conclusão:
A palavra aleatória deriva da palavra latina
alea que significa sorte, azar, risco ou
acaso.
«Alea jacta est.»- a sorte está lançada.
Para o estudo da teoria dasPara o estudo da teoria das
probabilidades só as experiênciasprobabilidades só as experiências
Aleatórias interessam, aquelasAleatórias interessam, aquelas
que dependem do acaso.que dependem do acaso.

8. Experiências
• Lançamento de uma moeda
• Lançamento de um dado
• Totoloto
• Estado do tempo para a
semana
• Extracção de uma carta
• Tempo que uma lâmpada irá
durar
• Furar um balão cheio
• Deixar cair um prego
num copo de água
• Calcular a área de
quadrado de lado 9 cm
À partida não sabemos o
resultado
À partida já
conhecemos o
resultado

9. Termos e conceitos
Conjunto de Resultados ou Espaço Amostral
Consideremos a experiência seguinte.
“No lançamento de um dado perfeito com as faces numeradas de 1 a 6,
ver qual a face que fica voltada para cima.”
À partida já sabemos quais as opções que podemos obter –
faces: 1, 2, 3, 4, 5 ou 6.
Então, { }6,5,4,3,2,1
é o conjunto de resultados ou o espaço amostral desta experiência.
Esta experiência tem 6 resultados possíveis ou 6 casos possíveis.

10. Definição:
Conjunto de resultados ou espaço amostral – é o conjunto formado
por todos os resultados possíveis de uma experiência aleatória.
Representa-se por E, S ou .Ω
.
{ }6,5,4,3,2,1===Ω SE
EXPERIÊNCIA 2: Jogo de futebol
S = {Vitória, Empate, Derrota }
EXPERIÊNCIA 3: Tirar uma bola de Totoloto
E = {1, 2, 3, ... ,47, 48, 49 }
EXPERIÊNCIA 4: Lançamento de um rapa
= {rapa, tira, deixa ,põe}Ω
R

11. Com o espaço amostral, podem formar-se acontecimentos.
Acontecimentos que se podem formar com a experiência
do lançamento do dado.
AcontecimentosAcontecimentos
Por exemplo:
A: «Sair face 6.»
B: «Sair face 3 e face 4.»
C: «Sair face com um número ímpar.»
D: «Sair face com um número menor que cinco.»
E: «Sair um divisor de 6.»
F: «Sair face com um número ímpar ou par.»
Quantos casos há para cadaQuantos casos há para cada
um dos acontecimentos?um dos acontecimentos?
A={ }6 1 caso
B={ } 0 casos0 casos

12. Então, podemos concluir que:
Acontecimento – é qualquer subconjunto do espaço amostral
(conjunto de resultados) de uma experiência aleatória.
Dá exemplo de um acontecimento na realização da seguinte
experiência aleatória:
“Extracção de uma bola de um saco, que contém: 5 bolas
vermelhas, 2 brancas e 3 azuis.”

13. CLASSIFICAÇÃO DOS ACONTECIMENTOSCLASSIFICAÇÃO DOS ACONTECIMENTOS
Tendo em conta os 6 acontecimentos anteriores, relativos à experiência
“Lançamento de um dada perfeito”, podemos dizer que:
A: «Sair face 6.»
B: «Sair face 3 e face 4.»
C: «Sair face com um número ímpar.»
A={ }6
B= { }
•O acontecimento A é um acontecimento elementar pouco provável.
•O acontecimento B é um acontecimento impossível.
C={ }5,3,1
•O acontecimento C é um acontecimento composto e provável.

14. D: «Sair face com um número menor que cinco.»
F: «Sair face com um número ímpar ou par.»
•O acontecimentos D e E são acontecimentos compostos e muito prováveis
E: «Sair um divisor de 6.»
•O acontecimento F é um acontecimento certo.
{ }4,3,2,1=D
{ }6,3,2,1=E
{ }6,5,4,3,2,1=F

15. Conclusões:Conclusões:
Os acontecimentos podem ser
Elementares
Compostos

16. 





















sImpossívei
Pr
Certo
prováveisMuito
ováveis
prováveisPouco
Possíveis
ntosAcontecime

17. Efectuar todos os exercícios
das páginas 10 e 11 do manual
adoptado.
Individualmente

18. ACONTECIMENTOS EQUIPROVÁVEIS
O cálculo de probabilidades procura medir até que ponto se pode
esperar que ocorra um acontecimento.
Consideremos a seguinte experiência:
“No lançamento de um dado perfeito (ou equilibrado) anotar a face que
fica voltada para cima.”
Observação:
“Dado perfeito ou equilibrado”, significa que o dado não tem nenhum
“vício” que faça com que alguma face saia mais frequentemente do que
as outras. Se o dado for equilibrado ou perfeito então a probabilidade de
sair cada uma das faces é igual. Isto é,
( ) ( ) ( ) ( ) ( ) ( )654321 facePfacePfacePfacePfacePfaceP =====

19. Dois acontecimentos que têm a mesma probabilidade de
ocorrerem, dizem-se acontecimentos equiprováveis.
Definição:

20. Como calcular a probabilidade de um
acontecimento?
Lei de LAPLACE
1749 - 1827

21. Consideremos os acontecimentos relativos à experiência do lançamento
de um dado perfeito.
A:”sair face 5.” B:”sair face par.” C:”sair face maior ou igual a 3.”
Antes de calcularmos a probabilidade destes acontecimentos,
temos de conhecer duas situações:
{ }6,5,4,3,2,1=Ω O número de casos possíveis, 6.
1.ª
2.ª A outra situação, são os chamados casos favoráveis,
que variam de acordo com cada acontecimento.
A:”sair face 5.” { }5=A
Neste caso, só existe 1 caso favorável à ocorrência do acontecimento.
( ) %17
6
1
≈=AP

22. B:”sair face par.”
C:”sair face maior ou igual a 3.”
( ) %50
2
1
6
3
===BP
( ) %67
3
2
6
4
≈==CP

23. ( )
possíveiscasosdeNúmero
favoráveiscasosdeNúmero
AP =
Definição:
Se os acontecimentos elementares são equiprováveisequiprováveis e em número finito,
pode-se calcular a probabilidade de um acontecimento A usando uma
fórmula que tem o nome de Lei de Laplace.
A probabilidade de um acontecimento A, P(A), é igual ao quociente entre
O número de casos favoráveis ao acontecimento e o número de casos
possíveis.
A probabilidade de um acontecimento é um número que pode
apresentar-se sob a forma de fracção, de percentagem ou de
um numeral com vírgula.

24. Exercício:
Um “rapa” tem 4 faces - rapa, R; tira, T; põe, P; deixa, D, todas com
a mesma probabilidade de saírem num lançamento.
Ao lançar o “rapa”, qual a probabilidade de:
( )
4
1
"" =RsairP
( )
4
3
"" =RsairnãoP
( )
2
1
4
2
"" ==TouRsairP
a) sair R?
b) Não sair R?
c) Sair R ou T?

25. Efectuar os exercícios das
páginas 15,16 e 17 do manual
adoptado.