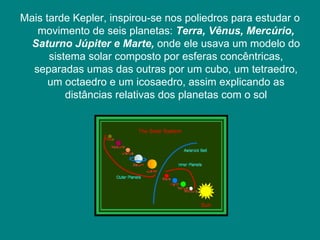
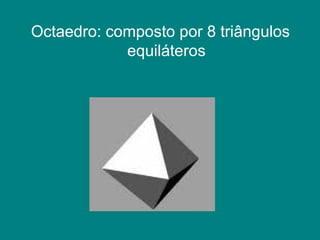
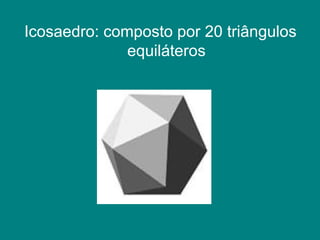
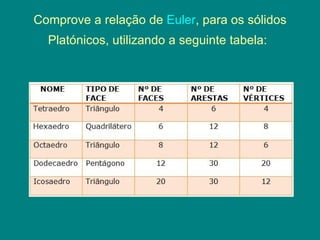
Os sólidos platônicos são os cinco sólidos regulares convexos descritos por Platão - o cubo, tetraedro, octaedro, dodecaedro e icosaedro. Cada sólido representava um elemento da natureza. Kepler mais tarde inspirou-se nos sólidos platônicos para estudar o movimento dos planetas.