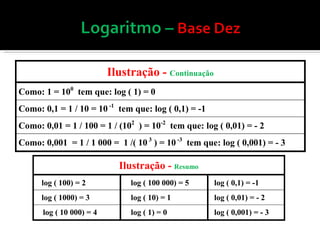
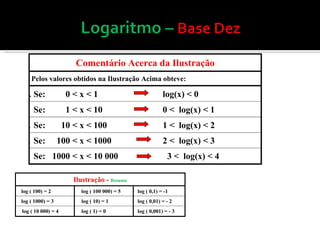
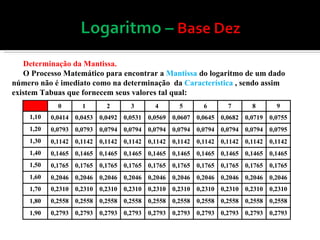
O documento discute logaritmos com bases especiais 10 e e, explicando que a base 10 é usada devido ao sistema numérico decimal e a base e é importante para estudos científicos. Ele também explica como calcular logaritmos usando tábuas, definindo a característica e mantissa e demonstrando exemplos de cálculos.

1. Logaritmo PARTE 5 –Bases Especiais.

2. Dois casos particulares de interesse para se ter logaritmos e de uso universal são: Base Dez – Se deve ao fato de que o Nosso Sistema de Numeração é o Sistema Decimal; Base e – e é um número irracional descoberto pelo matemático NEPER, ao qual a descrição de logaritmos em sua Base é de Total Interesse do Mundo Científico, pois neste sistema o estudo de fenômenos científicos se tornam mais amenos e compreensíveis.

3. No caso de logaritmos na Base Dez (10) dispensa-se o uso explícito da Base, ficando então subtendido, e assim a sua notação é:

6. Questionamento: Mas e quando x for Negativo  Conclusão para este caso: Recordemos: O Número é a Base elevado ao Valor do Logaritmo; Aqui: A Base é 10 (Dez); Assim: a) 10 elevado a um número positivo é um Número Positivo; b) 10 elevado a um Número Negativo é uma Fração em que: i) Numerador é 1; ii) Denominador é 10 elevado ao este número e é Positivo. Daí: Conclui que Para Números Negativos NÃO se calcula o Logaritmo. Logo: Logaritmo é SOMENTE para Números Positivos.

7. O Valor do Logaritmo, quando escrito sob a forma de um número decimal possui a característica: Pela Descrição já vista, para o caso de números maiores que 1, o valor do logaritmo na Base 10 é: Um número decimal (é real mas escrito na forma aproximada) ao qual pode ser escrito como: Um número Inteiro adicionado à parte decimal ( entre Zero e Um) e assim procedendo o valor do logaritmo é composto de: Parte Inteira : É denominado de CARACTERÍSTICA ; Parte Decimal ( < 1,0): é a MANTISSA .

8. Observando o quadro ao lado, tem que o valor da característica é: ZERO se o número está entre 1 e 9; UM se for entre 10 e 99; DOIS se entre 100 e 999; TRÊS se entre 1000 e 9999; Etc. Ou seja: A Característica é um identificador da Grandeza do Número e seu valor é: No caso de números maiores que 1 : A quantia de dígitos da Parte Inteira Subtraído de uma Unidade; Entre 0 e 1 : Será visto em outro momento.

9. Afinal de contas: O que é Realmente a Característica  Resposta: Como se sabe todo número pode ser escrito na Forma de um produto, onde suas parcelas são: Primeira: Um número decimal compreendido de Zero a Um; Segunda: Uma Potência Inteira de Dez. Exemplo. 01. 32,56 = 3,256x10 1 02. 1342,56 = 1,34256x10 3 03. 2,126 = 2,126x10 0 04. 0,00327 = 3,27x10 -3 E a característica é o expoente inteiro de 10. Motivo da Potência de Base 10: Aqui está estudando: Logaritmo Decimal

10. Afinal de contas: O que é Realmente a Característica  Resposta: Como se sabe todo número pode ser escrito na Forma de um produto, onde suas parcelas são: Primeira: Um número decimal compreendido de Zero a Um; Segunda: Uma Potência Inteira de Dez. Exemplo. 01. 32,56 = 3,256x10 1 02. 1342,56 = 1,34256x10 3 03. 2,126 = 2,126x10 0 04. 0,00327 = 3,27x10 -3 E a característica é o expoente inteiro de 10. Motivo da Potência de Base 10: Aqui está estudando: Logaritmo Decimal

11. Exemplo. Do exemplo anterior que foi: 01. 32,56 = 3,256x10 1 02. 1342,56 = 1,34256x10 3 03. 2,126 = 2,126x10 0 04. 0,00327 = 3,27x10 -3 Tem que cada característica é: 01. Um ( 10 1 ) 02. Três ( 10 3 ) 03. Zero (10 0 ) 04. Três Negativo (10 -3 ) Característica de Números entre Zero e UM. Pelo exemplo acima percebe que é a o Número de Posições após a virgula até o Primeiro digito diferente de Zero, porem é seu negativo. Com isto tem: se a = 0,0000 768 a sua característica é: - 5

12. Determinação da Mantissa. O Processo Matemático para encontrar a Mantissa do logaritmo de um dado número não é imediato como na determinação da Característica , sendo assim existem Tabuas que fornecem seus valores tal qual:

13. Uso e Interpretação A Primeira Coluna Indica a Parte Inteira e a Primeira Casa Decimal; A Primeira Linha indica a Segunda Casa Decimal; E cada valor descrito é o logaritmo do número lido, e como 1,00 < x < 9,99 , na realidade o que se tem é a Mantissa.

14. Exemplo de Leitura e Interpretação Olhando na tabela de logaritmo vem: a. log( 1,43 ) = 0,1465 ; b. log(1,10) = 0,0414 ; c. log(1,75) = 0,2310; d. log(1,99) = 0,2793. etc.

15. Comentário Sobre a Tabua: 01. Esta Tabua está totalmente restrita, ela foi apenas didática, existem livro de tabelas de logaritmo; 02. Por questão de comodidade foi tomado os números somente com duas casas decimais; 03. Nas Tabuas Gerais aparecem também as Partes Proporcionais , cujo objetivo é de inserir logaritmos de valores intermediários, aos quais na era da informática já não faz mais necessário pois seus valores se obtêm tanto em Planilhas como em calculadoras cientificas.

16. Cálculo de Logaritmo com o Auxílio da Tabua: Seja um número real positivo qualquer. Como se sabe, este número pode ser escrito na forma: x = a. 10 n aplicando logaritmo vem: log( x ) = log (a. 10 n ) = log ( a) + log (10 n ) log( x ) = log ( a) + n = n + log ( a) Em que: log ( a) é a Mantissa ; n é a característica. Isto Diz que: Para achar o logaritmo de um número qualquer com o uso da Tabua de Logaritmo: Soma: a Característica com a Mantissa .

17. Exemplo: Com o auxilio da Tábua de Logaritmo, ache cada valor que se pede: 01. log( 177 ) Solução Como: 177 = 1,77x 10 2 vem: log( 177 ) = log (1,77. 10 2 ) = log ( 1,77) + log (10 2 ) = log ( 1,77) + 2 Aqui: 2 é a Característica; log(1,77) é a Mantissa . Na tabua: log(1,77) = 0,2310 Logo: log(177) = 2 + 0,2310 Chega a: log(177) = 2,2310 Resposta: 2,2310

18. 02. log( 1 230 000 ) Solução Como: 1 130 000 = 1,13x 10 6 vem: log(1 130 000 ) = log (1,13x 10 6 ) = log ( 1,13) + log (10 6 ) = log ( 1,13) + 6 Característica: log(1,13); Mantissa: 6 . Na tabua: log(1,13) = 0,0531 Logo: log(1 130 000 ) = 6 + 0,0531 Chega a: log(1 130 000 ) = 6,0531 Resposta: 6,0531

19. 03. log( 0,000 15 ) Solução Como: 0,000 15 = 1,5x 10 -5 vem: log(0,000 15 ) = log (1,5x 10 -5 ) = log ( 1,5) + log (10 -5 ) = log ( 1,5) + ( - 5) Característica: log(1,5); Mantissa: - 5 . Na tabua: log(1,5) = 0,1765 Logo: log(0,000 15 ) = - 5 + 0,1765 Chega a: log(0,000 15 ) = - 4,8235 Resposta: - 4,8235

20. PARTE 5 –Bases Especiais FIM Prof. Gercino Monteiro Filho