03_Matematica Banco do Brasil.pdf

1
Banco do Brasil
Escriturário
1 - Números inteiros, racionais e reais; problemas de contagem. .......................................1
2 - Sistema legal de medidas. ...........................................................................................33
3 - Razões e proporções; divisão proporcional; regras de três simples e compostas;
porcentagens. ........................................................................................................................41
4 - Lógica proposicional. ...................................................................................................77
5 - Noções de conjuntos. ................................................................................................104
6 - Relações e funções; Funções polinomiais; Funções exponenciais e logarítmicas. ....115
7 - Matrizes. ....................................................................................................................148
8 - Determinantes. ..........................................................................................................158
9 - Sistemas lineares. .....................................................................................................173
10 - Sequências. 11 - Progressões aritméticas e progressões geométricas. ...................186
Olá Concurseiro, tudo bem?
Sabemos que estudar para concurso público não é tarefa fácil, mas acreditamos na sua
dedicação e por isso elaboramos nossa apostila com todo cuidado e nos exatos termos do
edital, para que você não estude assuntos desnecessários e nem perca tempo buscando
conteúdos faltantes. Somando sua dedicação aos nossos cuidados, esperamos que você
tenha uma ótima experiência de estudo e que consiga a tão almejada aprovação.
Pensando em auxiliar seus estudos e aprimorar nosso material, disponibilizamos o e-mail
professores@maxieduca.com.br para que possa mandar suas dúvidas, sugestões ou
questionamentos sobre o conteúdo da apostila. Todos e-mails que chegam até nós, passam
por uma triagem e são direcionados aos tutores da matéria em questão. Para o maior
aproveitamento do Sistema de Atendimento ao Concurseiro (SAC) liste os seguintes itens:
01. Apostila (concurso e cargo);
02. Disciplina (matéria);
03. Número da página onde se encontra a dúvida; e
04. Qual a dúvida.
Caso existam dúvidas em disciplinas diferentes, por favor, encaminhar em e-mails separados,
pois facilita e agiliza o processo de envio para o tutor responsável, lembrando que teremos até
cinco dias úteis para respondê-lo (a).
Não esqueça de mandar um feedback e nos contar quando for aprovado!
Bons estudos e conte sempre conosco!
1671811 E-book gerado especialmente para CARLA DIAS FERRAZ

1
CONJUNTO DOS NÚMEROS INTEIROS – Z
Definimos o conjunto dos números inteiros1
como a reunião do conjunto dos números naturais N = {0,
1, 2, 3, 4,..., n,...}, o conjunto dos opostos dos números naturais e o zero. Este conjunto é denotado pela
letra Z (Zahlen = número em alemão).
O conjunto dos números inteiros possui alguns subconjuntos notáveis:
Atenção: A nomenclatura utilizada abaixo pode interferir diretamente no contexto de uma questão,
tome muito cuidado ao interpreta-los, pois são todos diferentes (Z+ , Z_ , Z*).
- O conjunto dos números inteiros não nulos:
Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4,...}
Z* = Z – {0}
- O conjunto dos números inteiros não negativos:
Z+ = {0, 1, 2, 3, 4,...}
Z+ é o próprio conjunto dos números naturais: Z+ = N
- O conjunto dos números inteiros positivos:
Z*+ = {1, 2, 3, 4,...}
- O conjunto dos números inteiros não positivos:
Z_ = {..., -5, -4, -3, -2, -1, 0}
- O conjunto dos números inteiros negativos:
Z*- = {..., -5, -4, -3, -2, -1}
Módulo: chama-se módulo de um número inteiro a distância ou afastamento desse número até o zero,
na reta numérica inteira. Representa-se o módulo por | |.
O módulo de 0 é 0 e indica-se |0| = 0
O módulo de +7 é 7 e indica-se |+7| = 7
O módulo de –9 é 9 e indica-se |–9| = 9
O módulo de qualquer número inteiro, diferente de zero, é sempre positivo.
Números Opostos: Dois números inteiros são ditos opostos um do outro quando apresentam soma
zero; assim, os pontos que os representam distam igualmente da origem.
Exemplo: O oposto do número 3 é -3, e o oposto de -3 é 3, pois 3 + (-3) = (-3) + 3 = 0
No geral, dizemos que o oposto, ou simétrico, de a é – a, e vice-versa; particularmente o oposto de
zero é o próprio zero.
1
IEZZI, Gelson – Matemática - Volume Único
IEZZI, Gelson - Fundamentos da Matemática – Volume 01 – Conjuntos e Funções
1 - Números inteiros, racionais e reais; problemas de contagem.

2
Operações entre Números Inteiros
Adição de Números Inteiros
Para melhor entendimento desta operação, associaremos aos números inteiros positivos a ideia de
ganhar e aos números inteiros negativos a ideia de perder.
Ganhar 5 + ganhar 3 = ganhar 8 (+ 5) + (+ 3) = (+8)
Perder 3 + perder 4 = perder 7 (- 3) + (- 4) = (- 7)
Ganhar 8 + perder 5 = ganhar 3 (+ 8) + (- 5) = (+ 3)
Perder 8 + ganhar 5 = perder 3 (- 8) + (+ 5) = (- 3)
O sinal (+) antes do número positivo pode ser dispensado, mas o sinal (–) antes do número negativo
nunca pode ser dispensado.
Subtração de Números Inteiros
A subtração é empregada quando:
- Precisamos tirar uma quantidade de outra quantidade;
- Temos duas quantidades e queremos saber quanto uma delas tem a mais que a outra;
- Temos duas quantidades e queremos saber quanto falta a uma delas para atingir a outra.
A subtração é a operação inversa da adição.
Observe que em uma subtração o sinal do resultado é sempre do maior número!!!
4 + 5 = 9
4 – 5 = -1
Considere as seguintes situações:
1 - Na segunda-feira, a temperatura de Monte Sião passou de +3 graus para +6 graus. Qual foi a
variação da temperatura?
Esse fato pode ser representado pela subtração: (+6) – (+3) = +3
2 - Na terça-feira, a temperatura de Monte Sião, durante o dia, era de +6 graus. À Noite, a temperatura
baixou de 3 graus. Qual a temperatura registrada na noite de terça-feira?
Esse fato pode ser representado pela adição: (+6) + (–3) = +3
Se compararmos as duas igualdades, verificamos que (+6) – (+3) é o mesmo que (+6) + (–3).
Temos:
(+6) – (+3) = (+6) + (–3) = +3
(+3) – (+6) = (+3) + (–6) = –3
(–6) – (–3) = (–6) + (+3) = –3
Daí podemos afirmar: Subtrair dois números inteiros é o mesmo que adicionar o primeiro com o oposto
do segundo.
Fique Atento: todos parênteses, colchetes, chaves, números, ..., entre outros, precedidos de sinal
negativo, tem o seu sinal invertido, ou seja, é dado o seu oposto.
Ex.:
10 – (10+5) =
10 – (+15) =
10 – 15 =
- 5

3
Multiplicação de Números Inteiros
A multiplicação funciona como uma forma simplificada de uma adição quando os números são
repetidos. Poderíamos analisar tal situação como o fato de estarmos ganhando repetidamente alguma
quantidade, como por exemplo, ganhar 1 objeto por 30 vezes consecutivas, significa ganhar 30 objetos e
esta repetição pode ser indicada por um x, isto é: 1 + 1 + 1 ... + 1 + 1 = 30 x 1 = 30
Se trocarmos o número 1 pelo número 2, obteremos: 2 + 2 + 2 + ... + 2 + 2 = 30 x 2 = 60
Se trocarmos o número 2 pelo número -2, obteremos: (–2) + (–2) + ... + (–2) = 30 x (-2) = –60
Na multiplicação o produto dos números a e b, pode ser indicado por a x b, a . b ou ainda ab sem
nenhum sinal entre as letras.
Divisão de Números Inteiros
- Divisão exata de números inteiros.
Veja o cálculo:
(– 20) : (+ 5) = q  (+ 5) . q = (– 20)  q = (– 4)
Logo (– 20) : (+ 5) = - 4
Considerando os exemplos dados, concluímos que, para efetuar a divisão exata de um número inteiro
por outro número inteiro, diferente de zero, dividimos o módulo do dividendo pelo módulo do divisor.
Exemplo: (+7) : (–2) ou (–19) : (–5) são divisões que não podem ser realizadas em Z, pois o resultado
não é um número inteiro.
- No conjunto Z, a divisão não é comutativa, não é associativa e não tem a propriedade da existência
do elemento neutro.
- Não existe divisão por zero.
- Zero dividido por qualquer número inteiro, diferente de zero, é zero, pois o produto de qualquer
número inteiro por zero é igual a zero.
Exemplo: 0 : (–10) = 0 b) 0 : (+6) = 0 c) 0 : (–1) = 0
Regra de Sinais da Multiplicação e Divisão
→ Sinais iguais (+) (+); (-) (-) = resultado sempre positivo.
→ Sinais diferentes (+) (-); (-) (+) = resultado sempre negativo.
Potenciação de Números Inteiros
A potência xn
do número inteiro a, é definida como um produto de n fatores iguais. O número x é
denominado a base e o número n é o expoente. xn
= x . x . x . x ... x, x é multiplicado por x, n vezes.
Exemplos:
33
= (3) x (3) x (3) = 27
(-5)5
= (-5) x (-5) x (-5) x (-5) x (-5) = -3125
(-7)² = (-7) x (-7) = 49
(+9)² = (+9) x (+9) = 81
- Toda potência de base positiva é um número inteiro positivo.
Exemplo: (+3)2
= (+3) . (+3) = +9
- Toda potência de base negativa e expoente par é um número inteiro positivo.
Exemplo: (–8)2
= (–8) . (–8) = +64

4
- Toda potência de base negativa e expoente ímpar é um número inteiro negativo.
Exemplo: (–5)3
= (–5) . (–5) . (–5) = –125
- Propriedades da Potenciação:
1) Produtos de Potências com bases iguais: Conserva-se a base e somam-se os expoentes.
(–7)3
. (–7)6
= (–7)3+6
= (–7)9
2) Quocientes de Potências com bases iguais: Conserva-se a base e subtraem-se os expoentes.
(-13)8
: (-13)6
= (-13)8 – 6
= (-13)2
3) Potência de Potência: Conserva-se a base e multiplicam-se os expoentes.
[(-8)5
]2
= (-8)5 . 2
= (-8)10
4) Potência de expoente 1: É sempre igual à base.
(-8)1
= -8 e (+70)1
= +70
5) Potência de expoente zero e base diferente de zero: É igual a 1.
(+3)0
= 1 e (–53)0
= 1
Radiciação de Números Inteiros
A raiz n-ésima (de ordem n) de um número inteiro x é a operação que resulta em outro número inteiro
não negativo b que elevado à potência n fornece o número x. O número n é o índice da raiz enquanto que
o número x é o radicando (que fica sob o sinal do radical).
√𝑥
𝑛
= b
bn
= x
A raiz quadrada (de ordem 2) de um número inteiro x é a operação que resulta em outro número inteiro
não negativo que elevado ao quadrado coincide com o número x.
Atenção: Não existe a raiz quadrada de um número inteiro negativo no conjunto dos números
inteiros.
Erro comum: Frequentemente lemos em materiais didáticos e até mesmo ocorre em algumas aulas
aparecimento de:
9 = ± 3, mas isto está errado. O certo é: 9 = +3
Observamos que não existe um número inteiro não negativo que multiplicado por ele mesmo resulte
em um número negativo.
A raiz cúbica (de ordem 3) de um número inteiro x é a operação que resulta em outro número inteiro
que elevado ao cubo seja igual ao número x. Aqui não restringimos os nossos cálculos somente aos
números não negativos.
Exemplos:
(a)
3
8 = 2, pois 2³ = 8
(b)
3
8
 = –2, pois (–2)³ = -8
(c)
3
27 = 3, pois 3³ = 27
(d)
3
27
 = –3, pois (–3)³ = -27
Observação: Ao obedecer à regra dos sinais para o produto de números inteiros, concluímos que:
(1) Se o índice da raiz for par, não existe raiz de número inteiro negativo.
(2) Se o índice da raiz for ímpar, é possível extrair a raiz de qualquer número inteiro.

5
Propriedades da Adição e da Multiplicação dos números Inteiros
Para todo a, b e c ∈ 𝑍
1) Associativa da adição: (a + b) + c = a + (b + c)
2) Comutativa da adição: a + b = b + a
3) Elemento neutro da adição: a + 0 = a
4) Elemento oposto da adição: a + (-a) = 0
5) Associativa da multiplicação: (a.b).c = a.(b.c)
6) Comutativa da multiplicação: a.b = b.a
7) Elemento neutro da multiplicação: a.1 = a
8) Distributiva da multiplicação relativamente à adição: a.(b + c) = ab + ac
9) Distributiva da multiplicação relativamente à subtração: a.(b – c) = ab – ac
Atenção: tanto a adição como a multiplicação de um número natural por outro número natural, continua
como resultado um número natural.
Questões
01. (Fundação Casa – Agente Educacional – VUNESP) Para zelar pelos jovens internados e orientá-
los a respeito do uso adequado dos materiais em geral e dos recursos utilizados em atividades educativas,
bem como da preservação predial, realizou-se uma dinâmica elencando “atitudes positivas” e “atitudes
negativas”, no entendimento dos elementos do grupo. Solicitou-se que cada um classificasse suas
atitudes como positiva ou negativa, atribuindo (+4) pontos a cada atitude positiva e (-1) a cada atitude
negativa. Se um jovem classificou como positiva apenas 20 das 50 atitudes anotadas, o total de pontos
atribuídos foi
(A) 50.
(B) 45.
(C) 42.
(D) 36.
(E) 32.
02. (UEM/PR – Auxiliar Operacional – UEM) Ruth tem somente R$ 2.200,00 e deseja gastar a maior
quantidade possível, sem ficar devendo na loja.
Verificou o preço de alguns produtos:
TV: R$ 562,00
DVD: R$ 399,00
Micro-ondas: R$ 429,00
Geladeira: R$ 1.213,00
Na aquisição dos produtos, conforme as condições mencionadas, e pagando a compra em dinheiro, o
troco recebido será de:
(A) R$ 84,00
(B) R$ 74,00
(C) R$ 36,00
(D) R$ 26,00
(E) R$ 16,00
03. (BNDES – Técnico Administrativo – CESGRANRIO) Multiplicando-se o maior número inteiro
menor do que 8 pelo menor número inteiro maior do que - 8, o resultado encontrado será
(A) - 72
(B) - 63
(C) - 56
(D) - 49
(E) – 42

6
04. (Polícia Militar/MG - Assistente Administrativo - FCC) Em um jogo de tabuleiro, Carla e Mateus
obtiveram os seguintes resultados:
Ao término dessas quatro partidas,
(A) Carla perdeu por uma diferença de 150 pontos.
(B) Mateus perdeu por uma diferença de 175 pontos.
(C) Mateus ganhou por uma diferença de 125 pontos.
(D) Carla e Mateus empataram.
05. (Pref. de Palmas/TO – Técnico Administrativo Educacional – COPESE/UFT) Num determinado
estacionamento da cidade de Palmas há vagas para carros e motos. Durante uma ronda dos agentes de
trânsito, foi observado que o número total de rodas nesse estacionamento era de 124 (desconsiderando
os estepes dos veículos). Sabendo que haviam 12 motos no estacionamento naquele momento, é
CORRETO afirmar que estavam estacionados:
(A) 19 carros
(B) 25 carros
(C) 38 carros
(D) 50 carros
06. (Casa da Moeda) O quadro abaixo indica o número de passageiros num voo entre Curitiba e
Belém, com duas escalas, uma no Rio de Janeiro e outra em Brasília. Os números positivos indicam a
quantidade de passageiros que subiram no avião e os negativos, a quantidade dos que desceram em
cada cidade.
O número de passageiros que chegou a Belém foi:
(A) 362
(B) 280
(C) 240
(D) 190
(E) 135
07. (Pref.de Niterói/RJ) As variações de temperatura nos desertos são extremas. Supondo que
durantes o dia a temperatura seja de 45ºC e à noite seja de -10ºC, a diferença de temperatura entre o dia
e noite, em ºC será de:
(A) 10
(B) 35
(C) 45
(D) 50
(E) 55
08. (Pref.de Niterói/RJ) Um trabalhador deseja economizar para adquirir a vista uma televisão que
custa R$ 420,00. Sabendo que o mesmo consegue economizar R$ 35,00 por mês, o número de meses
que ele levará para adquirir a televisão será:
(A) 6
(B) 8
(C) 10
(D) 12
(E) 15

7
09. (Pref.de Niterói/RJ) Um estudante empilhou seus livros, obtendo uma única pilha 52cm de altura.
Sabendo que 8 desses livros possui uma espessura de 2cm, e que os livros restantes possuem espessura
de 3cm, o número de livros na pilha é:
(A) 10
(B) 15
(C) 18
(D) 20
(E) 22
10. (FINEP – Assistente Administrativo – CESGRANRIO) Um menino estava parado no oitavo
degrau de uma escada, contado a partir de sua base (parte mais baixa da escada). A escada tinha 25
degraus. O menino subiu mais 13 degraus. Logo em seguida, desceu 15 degraus e parou novamente.
A quantos degraus do topo da escada ele parou?
(A) 8
(B) 10
(C) 11
(D) 15
(E) 19
Comentários
01. Resposta: A
50-20=30 atitudes negativas
20.4=80
30.(-1)=-30
80-30=50
02. Resposta: D
Geladeira + Micro-ondas + DVD = 1213 + 429 + 399 = 2041
Geladeira + Micro-ondas + TV = 1213 + 429 + 562 = 2204, extrapola o orçamento
Geladeira + TV + DVD = 1213 + 562 + 399 = 2174, é a maior quantidade gasta possível dentro do
orçamento.
Troco:2200 – 2174 = 26 reais
03. Resposta: D
Maior inteiro menor que 8 é o 7
Menor inteiro maior que - 8 é o - 7.
Portanto: 7(- 7) = - 49
04. Resposta: C
Carla: 520 – 220 – 485 + 635 = 450 pontos
Mateus: - 280 + 675 + 295 – 115 = 575 pontos
Diferença: 575 – 450 = 125 pontos
05. Resposta: B
Moto: 2 rodas
Carro: 4
12.2=24
124-24=100
100/4=25 carros
06. Resposta: D
240 - 194 + 158 - 108 + 94 = 190
07. Resposta: E
45 – (- 10) = 55

8
08. Resposta: D
420: 35 = 12 meses
09. Resposta: D
São 8 livros de 2 cm: 8.2 = 16 cm
Como eu tenho 52 cm ao todo e os demais livros tem 3 cm, temos:
52 - 16 = 36 cm de altura de livros de 3 cm
36 : 3 = 12 livros de 3 cm
O total de livros da pilha: 8 + 12 = 20 livros ao todo.
10. Resposta: E
8 + 13 = 21
21– 15 = 6
25 – 6 = 19
CONJUNTO DOS NÚMEROS RACIONAIS – Q
Um número racional2
é o que pode ser escrito na forma
n
m
, onde m e n são números inteiros, sendo
que n deve ser diferente de zero. Frequentemente utilizamos m/n para significar a divisão de m por n.
Como podemos observar, números racionais podem ser obtidos através da razão entre dois números
inteiros, razão pela qual, o conjunto de todos os números racionais é denotado por Q. Assim, é comum
encontrarmos na literatura a notação:
Q = {
n
m
: m e n em Z, n diferente de zero}
No conjunto Q destacamos os seguintes subconjuntos:
Atenção: A nomenclatura utilizada abaixo pode interferir diretamente no contexto de uma
questão, tome muito cuidado ao interpreta-los, pois são todos diferentes (Q+ , Q_ , Q*).
- Q* = conjunto dos racionais não nulos;
- Q+ = conjunto dos racionais não negativos;
- Q*+ = conjunto dos racionais positivos;
- Q _ = conjunto dos racionais não positivos;
- Q*_ = conjunto dos racionais negativos.
Representação Decimal das Frações
Tomemos um número racional
q
p
, tal que p não seja múltiplo de q. Para escrevê-lo na forma decimal,
basta efetuar a divisão do numerador pelo denominador.
Nessa divisão podem ocorrer dois casos:
1º - O numeral decimal obtido possui, após a vírgula, um número finito de algarismos. Decimais Exatos:
2
IEZZI, Gelson - Matemática- Volume Único
IEZZI, Gelson - Fundamentos da Matemática – Volume 1 – Conjuntos e Funções
http://mat.ufrgs.br

9
2º - O numeral decimal obtido possui, após a vírgula, infinitos algarismos (nem todos nulos), repetindo-
se periodicamente Decimais Periódicos ou Dízimas Periódicas:
Existem frações muito simples que são representadas por formas decimais infinitas, com uma
característica especial:
Aproveitando o exemplo acima temos 0,333... = 3. 1/101
+ 3 . 1/102
+ 3 . 1/103
+ 3 . 1/104
...
Representação Fracionária dos Números Decimais
Trata-se do problema inverso, estando o número racional escrito na forma decimal, procuremos
escrevê-lo na forma de fração. Temos dois casos:
1º Transformamos o número em uma fração cujo numerador é o número decimal sem a vírgula e o
denominador é composto pelo numeral 1, seguido de tantos zeros quantas forem as casas decimais do
número decimal dado:
2º Devemos achar a fração geratriz da dízima dada; para tanto, vamos apresentar o procedimento
através de alguns exemplos:
a) Seja a dízima 0, 333...
Veja que o período que se repete é apenas 1(formado pelo 3)  então vamos colocar um 9 no
denominador e repetir no numerador o período.

10
Assim, a geratriz de 0,333... é a fração
9
3
.
b) Seja a dízima 5, 1717...
O período que se repete é o 17, logo dois noves no denominador (99). Observe também que o 5 é a
parte inteira, logo ele vem na frente:
5
17
99
→ 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑓𝑟𝑎çã𝑜 𝑚𝑖𝑠𝑡𝑎, 𝑡𝑟𝑎𝑛𝑓𝑜𝑟𝑚𝑎𝑛𝑑𝑜 → (5.99 + 17) = 512, 𝑙𝑜𝑔𝑜 ∶
512
99
Assim, a geratriz de 5,1717... é a fração
99
512
.
Neste caso para transformarmos uma dízima periódica simples em fração, basta utilizarmos o
dígito 9 no denominador de acordo com a quantidade de dígitos que tiver o período da dízima.
c) Seja a dízima 1, 23434...
O número 234 é a junção do anteperíodo com o período. Neste caso dizemos que a dízima periódica
é composta, pois existe uma parte que não se repete e outra que se repete. Temos então um anteperíodo
(2) e o período (34). Ao subtrairmos deste número o anteperíodo (234-2), obtemos 232 no qual será o
numerador. O denominador é formado por tantos dígitos 9 – que correspondem ao período, neste caso
99 (dois noves) – e pelo dígito 0 – que correspondem a tantos dígitos tiverem o anteperíodo, neste caso
0 (um zero).
1
232
990
→ 𝑡𝑒𝑚𝑜𝑠 𝑢𝑚𝑎 𝑓𝑟𝑎çã𝑜 𝑚𝑖𝑠𝑡𝑎, 𝑡𝑟𝑎𝑛𝑓𝑜𝑟𝑚𝑎𝑛𝑑𝑜 − 𝑎 → (1.990 + 232) = 1222, 𝑙𝑜𝑔𝑜 ∶
1222
990
Simplificando por 2, obtemos x =
495
611
, que será a fração geratriz da dízima 1, 23434...
Módulo ou valor absoluto: É a distância do ponto que representa esse número ao ponto de abscissa
zero.
Exemplos:
1) Módulo de –
2
3
é
2
3
. Indica-se
2
3
 =
2
3
2) Módulo de +
2
3
é
2
3
. Indica-se
2
3
 =
2
3
Números Opostos: Dizemos que –
2
3
e
2
3
são números racionais opostos ou simétricos e cada um
deles é o oposto do outro. As distâncias dos pontos –
2
3
e
2
3
ao ponto zero da reta são iguais.

11
Inverso de um Número Racional
(
𝒂
𝒃
)
−𝒏
, 𝒂 ≠ 𝟎 = (
𝒃
𝒂
)
𝒏
, 𝒃 ≠ 𝟎
Representação geométrica dos Números Racionais
Observa-se que entre dois inteiros consecutivos existem infinitos números racionais.
Soma (Adição) de Números Racionais
Como todo número racional é uma fração ou pode ser escrito na forma de uma fração, definimos a
adição entre os números racionais
b
a
e
d
c
, da mesma forma que a soma de frações, através de:
Subtração de Números Racionais
A subtração de dois números racionais p e q é a própria operação de adição do número p com o
oposto de q, isto é: p – q = p + (–q), onde p =
b
a
e q =
d
c
.
Multiplicação (Produto) de Números Racionais
Como todo número racional é uma fração ou pode ser escrito na forma de uma fração, definimos o
produto de dois números racionais
b
a
e
d
c
, da mesma forma que o produto de frações, através de:
Para realizar a multiplicação de números racionais, devemos obedecer à mesma regra de sinais que
vale em toda a Matemática:
Podemos assim concluir que o produto de dois números com o mesmo sinal é positivo, mas o
produto de dois números com sinais diferentes é negativo.
Divisão (Quociente) de Números Racionais
A divisão de dois números racionais p e q é a própria operação de multiplicação do número p pelo
inverso de q, isto é: p ÷ q = p × q-1
𝒂
𝒃
:
𝒄
𝒅
=
𝒂
𝒃
.
𝒅
𝒄

12
Potenciação de Números Racionais
A potência qn
do número racional q é um produto de n fatores iguais. O número q é denominado a
base e o número n é o expoente.
qn
= q × q × q × q × ... × q, (q aparece n vezes)
Exemplos:
Propriedades da Potenciação:
1) Toda potência com expoente 0 é igual a 1.
2) Toda potência com expoente 1 é igual à própria base.
3) Toda potência com expoente negativo de um número racional diferente de zero é igual a outra
potência que tem a base igual ao inverso da base anterior e o expoente igual ao oposto do expoente
anterior.
4) Toda potência com expoente ímpar tem o mesmo sinal da base.
5) Toda potência com expoente par é um número positivo.
6) Produto de potências de mesma base. Para reduzir um produto de potências de mesma base a uma
só potência, conservamos a base e somamos os expoentes.
7) Divisão de potências de mesma base. Para reduzir uma divisão de potências de mesma base a uma
só potência, conservamos a base e subtraímos os expoentes.
8) Potência de Potência. Para reduzir uma potência de potência a uma potência de um só expoente,
conservamos a base e multiplicamos os expoentes.
Radiciação de Números Racionais
Se um número representa um produto de dois ou mais fatores iguais, então cada fator é chamado raiz
do número.

13
Exemplos:
1)
9
1
Representa o produto
3
1
.
3
1
ou
2
3
1






.Logo,
3
1
é a raiz quadrada de
9
1
.
Indica-se
9
1
=
3
1
2) 0,216 Representa o produto 0,6 . 0,6 . 0,6 ou (0,6)3
. Logo, 0,6 é a raiz cúbica de 0,216. Indica-se
3
216
,
0 = 0,6.
Um número racional, quando elevado ao quadrado, dá o número zero ou um número racional positivo.
Logo, os números racionais negativos não têm raiz quadrada no conjunto dos números racionais.
Por exemplo, o número
9
100
 não tem raiz quadrada em Q, pois tanto
3
10
 como
3
10
 , quando
elevados ao quadrado, dão
9
100
.
Já um número racional positivo, só tem raiz quadrada no conjunto dos números racionais se ele for um
quadrado perfeito.
E o número
3
2
não tem raiz quadrada em Q, pois não existe número racional que elevado ao quadrado
dê
3
2
.
Questões
01. (Pref. Jundiaí/SP– Agente de Serviços Operacionais – MAKIYAMA) Na escola onde estudo, ¼
dos alunos tem a língua portuguesa como disciplina favorita, 9/20 têm a matemática como favorita e os
demais têm ciências como favorita. Sendo assim, qual fração representa os alunos que têm ciências como
disciplina favorita?
(A) 1/4
(B) 3/10
(C) 2/9
(D) 4/5
(E) 3/2
02. (Fundação CASA – Agente de Apoio Operacional – VUNESP) De um total de 180 candidatos,
2/5 estudam inglês, 2/9 estudam francês, 1/3 estuda espanhol e o restante estuda alemão. O número de
candidatos que estuda alemão é:
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.
03. (Fundação CASA – Agente de Apoio Operacional – VUNESP) Em um estado do Sudeste, um
Agente de Apoio Operacional tem um salário mensal de: salário-base R$ 617,16 e uma gratificação de
R$ 185,15. No mês passado, ele fez 8 horas extras a R$ 8,50 cada hora, mas precisou faltar um dia e foi
descontado em R$ 28,40. No mês passado, seu salário totalizou
(A) R$ 810,81.
(B) R$ 821,31.
(C) R$ 838,51.
(D) R$ 841,91.
(E) R$ 870,31.

14
04. (Pref. Niterói) Simplificando a expressão abaixo:
1,3333…+
3
2
1,5+
4
3
Obtém-se
(A) ½.
(B) 1.
(C) 3/2.
(D) 2.
(E) 3.
05. (SABESP – Aprendiz – FCC) Em um jogo matemático, cada jogador tem direito a 5 cartões
marcados com um número, sendo que todos os jogadores recebem os mesmos números. Após todos os
jogadores receberem seus cartões, aleatoriamente, realizam uma determinada tarefa que também é
sorteada. Vence o jogo quem cumprir a tarefa corretamente. Em uma rodada em que a tarefa era colocar
os números marcados nos cartões em ordem crescente, venceu o jogador que apresentou a sequência
(A) −4; −1; √16; √25;
14
3
(B) −1; −4; √16;
14
3
; √25
(C) −1; −4;
14
3
; √16; √25
(D) −4; −1; √16;
14
3
; √25
(E)−4; −1;
14
3
; √16; √25
06. (SABESP – Agente de Saneamento Ambiental – FCC) Somando-se certo número positivo x ao
numerador, e subtraindo-se o mesmo número x do denominador da fração 2/3 obtém-se como resultado,
o número 5. Sendo assim, x é igual a
(A) 52/25.
(B) 13/6.
(C) 7/3.
(D) 5/2.
(E) 47/23.
07. (SABESP – Aprendiz – FCC) Mariana abriu seu cofrinho com 120 moedas e separou-as:
− 1 real: ¼ das moedas
− 50 centavos: 1/3 das moedas
− 25 centavos: 2/5 das moedas
− 10 centavos: as restantes
Mariana totalizou a quantia contida no cofre em
(A) R$ 62,20.
(B) R$ 52,20.
(C) R$ 50,20.
(D) R$ 56,20.
(E) R$ 66,20.
08. (PM/SE – Soldado 3ªclasse – FUNCAB) Numa operação policial de rotina, que abordou 800
pessoas, verificou-se que 3/4 dessas pessoas eram homens e 1/5 deles foram detidos. Já entre as
mulheres abordadas, 1/8 foram detidas.
Qual o total de pessoas detidas nessa operação policial?
(A) 145
(B) 185
(C) 220
(D) 260
(E) 120
09. (Pref. Jundiaí/SP – Agente de Serviços Operacionais – MAKIYAMA) Quando perguntado sobre
qual era a sua idade, o professor de matemática respondeu:
“O produto das frações 9/5 e 75/3 fornece a minha idade!”.

15
Sendo assim, podemos afirmar que o professor tem:
(A) 40 anos.
(B) 35 anos.
(C) 45 anos.
(D) 30 anos.
(E) 42 anos.
Comentários
01. Alternativa: B.
Somando português e matemática:
1
4
+
9
20
=
5 + 9
20
=
14
20
=
7
10
O que resta gosta de ciências:
1 −
7
10
=
3
10
02. Alternativa: C.
2
5
+
2
9
+
1
3
Mmc(3,5,9)=45
18+10+15
45
=
43
45
O restante estuda alemão: 2/45
180 ∙
2
45
= 8
03. Alternativa: D.
𝑠𝑎𝑙á𝑟𝑖𝑜 𝑚𝑒𝑛𝑠𝑎𝑙: 617,16 + 185,15 = 802,31
ℎ𝑜𝑟𝑎𝑠 𝑒𝑥𝑡𝑟𝑎𝑠: 8,5 ∙ 8 = 68
𝑚ê𝑠 𝑝𝑎𝑠𝑠𝑎𝑑𝑜: 802,31 + 68,00 − 28,40 = 841,91
Salário foi R$ 841,91.
04. Alternativa: B.
1,3333...= 12/9 = 4/3
1,5 = 15/10 = 3/2
4
3 +
3
2
3
2
+
4
3
=
17
6
17
6
= 1
05. Alternativa: D.
√16 = 4
√25 = 5
14
3
= 4,67
A ordem crescente é: −4; −1; √16;
14
3
; √25
06. Alternativa: B.
Lá vem o tal do “x” né, mas analise o seguinte, temos a fração
2
3
, aí ele disse o seguinte: Somando-se
certo número positivo x ao numerador, e subtraindo-se o mesmo número x do denominador da fração,
logo devemos somar “x” no 2 e subtrair “x” de 3, ficando:
2 + x
3 − x
Isso é igual a 5, assim teremos formada nossa equação com números racionais!
2+x
3−x
= 5, para resolver devemos multiplicar em cruz (como não tem ninguém no denominador do 5,
devemos colocar o 1).

16
1.(2 + x) = 5.(3 – x)
Aplicando a propriedade distributiva:
2 + x = 15 – 5x
Letra para um lado e número para o outro, não esquecendo que quando troca de lado inverte o número.
x + 5x = 15 – 2
6x = 13
x =
13
6
Portanto a alternativa correta é a “B”.
07. Alternativa: A.
1 𝑟𝑒𝑎𝑙: 120 ∙
1
4
= 30 𝑚𝑜𝑒𝑑𝑎𝑠
50 𝑐𝑒𝑛𝑡𝑎𝑣𝑜𝑠:
1
3
∙ 120 = 40 𝑚𝑜𝑒𝑑𝑎𝑠
25 𝑐𝑒𝑛𝑡𝑎𝑣𝑜𝑠:
2
5
∙ 120 = 48 𝑚𝑜𝑒𝑑𝑎𝑠
10 𝑐𝑒𝑛𝑡𝑎𝑣𝑜𝑠: 120 − 118 𝑚𝑜𝑒𝑑𝑎𝑠 = 2 𝑚𝑜𝑒𝑑𝑎𝑠
30 + 40 ∙ 0,5 + 48 ∙ 0,25 + 2 ∙ 0,10 = 62,20
Mariana totalizou R$ 62,20.
08. Alternativa: A.
Este problema é clássico na utilização de frações, primeiro vamos calcular a quantidade de homens e
mulheres abordadas:
Total: 800
Homens:
3
4
sendo assim devemos encontrar
3
4
𝑑𝑒 800 = 3𝑥800 = 2400, 𝑒 2400 ∶ 4 = 600
Se temos 600 homens, significa que 200 são as mulheres, pois o total é 800, agora vamos calcular os
detidos!
Homens detidos:
1
5
de 600, logo 600 x 1 = 600 e 600 : 5 = 120, portanto 120 homens detidos.
Mulheres detidas:
1
8
de 200, logo 200 x 1 = 200 e 200 : 8 = 25, portanto 25 mulheres detidas.
O enunciado pede o total de pessoas detidas nessa operação policial, logo 120 + 25 = 145, o que nos
remete a alternativa “A”.
09. Alternativa: C.
9
5
∙
75
3
=
675
15
= 45 𝑎𝑛𝑜𝑠
CONJUNTO DOS NÚMEROS REAIS - R
O conjunto dos números reais3
R é uma expansão do conjunto dos números racionais que engloba
não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
Assim temos:
R = Q U I , sendo Q ∩ I = Ø ( Se um número real é racional, não será irracional, e vice-versa).
Lembrando que N Ϲ Z Ϲ Q , podemos construir o diagrama abaixo:
3
IEZZI, Gelson - Fundamentos da Matemática Elementar – Vol. 01 – Conjuntos e Funções

17
O conjunto dos números reais apresenta outros subconjuntos importantes:
- Conjunto dos números reais não nulos: R* = {x ϵ R| x ≠ 0}
- Conjunto dos números reais não negativos: R+ = {x ϵ R| x ≥ 0}
- Conjunto dos números reais positivos: R*+ = {x ϵ R| x > 0}
- Conjunto dos números reais não positivos: R- = {x ϵ R| x ≤ 0}
- Conjunto dos números reais negativos: R*- = {x ϵ R| x < 0}
Representação Geométrica dos números reais
Ordenação dos números reais
A representação dos números reais permite definir uma relação de ordem entre eles. Os números reais
positivos, são maiores que zero e os negativos, menores que zero. Expressamos a relação de ordem da
seguinte maneira:
Dados dois números Reais a e b,
a ≤ b ↔ b – a ≥ 0
Exemplo: -15 ≤ 5 ↔ 5 - ( - 15) ≥ 0
5 + 15 ≥ 0
Intervalos reais
O conjunto dos números reais possui também subconjuntos, denominados intervalos, que são
determinados por meio de desiguladades. Sejam os números a e b , com a < b.
Em termos gerais temos:
- A bolinha aberta = a intervalo aberto (estamos excluindo aquele número), utilizamos os símbolos:
> ;< ou ] ; [
- A bolinha fechada = a intervalo fechado (estamos incluindo aquele número), utilizamos os símbolos:
≥ ; ≤ ou [ ; ]
Podemos utilizar ( ) no lugar dos [ ] , para indicar as extremidades abertas dos intervalos.

18
Às vezes, aparecem situações em que é necessário registrar numericamente variações de valores em
sentidos opostos, ou seja, maiores ou acima de zero (positivos), como as medidas de temperatura ou
reais em débito, em haver e etc. Esses números, que se estendem indefinidamente, tanto para o lado
direito (positivos) como para o lado esquerdo (negativos), são chamados números relativos.
Valor absoluto de um número relativo é o valor do número que faz parte de sua representação, sem o
sinal.
Valor simétrico de um número é o mesmo numeral, diferindo apenas o sinal.
Operações com números relativos
1) Adição e subtração de números relativos
a) Se os numerais possuem o mesmo sinal, basta adicionar os valores absolutos e conservar o sinal.
b) Se os numerais possuem sinais diferentes, subtrai-se o numeral de menor valor e dá-se o sinal do
maior numeral.
Exemplos:
3 + 5 = 8
4 - 8 = - 4
- 6 - 4 = - 10
- 2 + 7 = 5
2) Multiplicação e divisão de números relativos
a) O produto e o quociente de dois números relativos de mesmo sinal são sempre positivos.
b) O produto e o quociente de dois números relativos de sinais diferentes são sempre negativos.
Exemplos:
- 3 x 8 = - 24
- 20 (-4) = + 5
- 6 x (-7) = + 42
28 2 = 14
Questões
01. (EBSERH/ HUPAA – UFAL – Analista Administrativo – Administração – IDECAN) Mário
começou a praticar um novo jogo que adquiriu para seu videogame. Considere que a cada partida ele
conseguiu melhorar sua pontuação, equivalendo sempre a 15 pontos a menos que o dobro marcado na
partida anterior. Se na quinta partida ele marcou 3.791 pontos, então, a soma dos algarismos da
quantidade de pontos adquiridos na primeira partida foi igual a
(A) 4.
(B) 5.
(C) 7.
(D) 8.
(E) 10.
02. (Pref. Guarujá/SP – SEDUC – Professor de Matemática – CAIPIMES) Considere m um número
real menor que 20 e avalie as afirmações I, II e III:
I- (20 – m) é um número menor que 20.
II- (20 m) é um número maior que 20.
III- (20 m) é um número menor que 20.
É correto afirmar que:
(A) I, II e III são verdadeiras.
(B) apenas I e II são verdadeiras.
(C) I, II e III são falsas.
(D) apenas II e III são falsas.

19
03. (Pref. Guarujá/SP – SEDUC – Professor de Matemática – CAIPIMES) Na figura abaixo, o ponto
que melhor representa a diferença
3
4
−
1
2
na reta dos números reais é:
(A) P.
(B) Q.
(C) R.
(D) S.
04. (TJ/PR - Técnico Judiciário – TJ/PR) Uma caixa contém certa quantidade de lâmpadas. Ao retirá-
las de 3 em 3 ou de 5 em 5, sobram 2 lâmpadas na caixa.
Entretanto, se as lâmpadas forem removidas de 7 em 7, sobrará uma única lâmpada. Assinale a
alternativa correspondente à quantidade de lâmpadas que há na caixa, sabendo que esta comporta um
máximo de 100 lâmpadas.
(A) 36.
(B) 57.
(C) 78.
(D) 92.
05. (MP/SP – Auxiliar de Promotoria I – Administrativo – VUNESP) Para ir de sua casa à escola,
Zeca percorre uma distância igual a
3
4
da distância percorrida na volta, que é feita por um trajeto diferente.
Se a distância percorrida por Zeca para ir de sua casa à escola e dela voltar é igual a
7
5
de um quilômetro,
então a distância percorrida por Zeca na ida de sua casa à escola corresponde, de um quilômetro, a
(A)
2
3
(B)
3
4
(C)
1
2
(D)
4
5
(E)
3
5
06. (TJ/SP - Auxiliar de Saúde Judiciário - Auxiliar em Saúde Bucal – VUNESP) Para numerar as
páginas de um livro, uma impressora gasta 0,001 mL por cada algarismo impresso. Por exemplo, para
numerar as páginas 7, 58 e 290 gasta-se, respectivamente, 0,001 mL, 0,002 mL e 0,003 mL de tinta. O
total de tinta que será gasto para numerar da página 1 até a página 1 000 de um livro, em mL, será
(A) 1,111.
(B) 2,003.
(C) 2,893.
(D) 1,003.
(E) 2,561.
07. (Câmara de São Paulo/SP – Técnico Administrativo – FCC) Um funcionário de uma empresa
deve executar uma tarefa em 4 semanas. Esse funcionário executou 3/8 da tarefa na 1a semana. Na 2 a
semana, ele executou 1/3 do que havia executado na 1a semana. Na 3a e 4a semanas, o funcionário
termina a execução da tarefa e verifica que na 3a semana executou o dobro do que havia executado na
4 a semana. Sendo assim, a fração de toda a tarefa que esse funcionário executou na 4ª semana é igual
a
(A) 5/16.
(B) 1/6.
(C) 8/24.
(D)1/ 4.
(E) 2/5.

20
08. (CODAR – Coletor de lixo reciclável – EXATUS/2016) Numa divisão com números inteiros, o
resto vale 5, o divisor é igual ao resto somado a 3 unidades e o quociente é igual ao dobro do divisor.
Assim, é correto afirmar que o valor do dividendo é igual a:
(A) 145.
(B) 133.
(C) 127.
(D) 118.
09. (METRÔ – Assistente Administrativo Júnior – FCC) Quatro números inteiros serão sorteados.
Se o número sorteado for par, ele deve ser dividido por 2 e ao quociente deve ser acrescido 17. Se o
número sorteado for ímpar, ele deve ser dividido por seu maior divisor e do quociente deve ser subtraído
15. Após esse procedimento, os quatro resultados obtidos deverão ser somados. Sabendo que os
números sorteados foram 40, 35, 66 e 27, a soma obtida ao final é igual a
(A) 87.
(B) 59.
(C) 28.
(D) 65.
(E) 63.
10. (UNESP – Assistente de Informática I – VUNESP) O valor de uma aposta em certa loteria foi
repartido em cotas iguais. Sabe-se que a terça parte das cotas foi dividida igualmente entre Alex e Breno,
que Carlos ficou com a quarta parte das cotas, e que Denis ficou com as 5 cotas restantes. Essa aposta
foi premiada com um determinado valor, que foi repartido entre eles de forma diretamente proporcional
ao número de cotas de cada um. Dessa forma, se Breno recebeu R$ 62.000,00, então Carlos recebeu
(A) R$ 74.000,00.
(B) R$ 93.000,00.
(C) R$ 98.000,00.
(D) R$ 102.000,00.
(E) R$ 106.000,00.
Comentários
01. Alternativa: D.
Pontuação atual = 2 . partida anterior – 15
* 4ª partida: 3791 = 2.x – 15
2.x = 3791 + 15
x = 3806 / 2
x = 1903
* 3ª partida: 1903 = 2.x – 15
2.x = 1903 + 15
x = 1918 / 2
x = 959
* 2ª partida: 959 = 2.x – 15
2.x = 959 + 15
x = 974 / 2
x = 487
* 1ª partida: 487 = 2.x – 15
2.x = 487 + 15
x = 502 / 2
x = 251
Portanto, a soma dos algarismos da 1ª partida é 2 + 5 + 1 = 8.
02. Alternativa: C.
I. Falso, pois m é Real e pode ser negativo.
II. Falso, pois m é Real e pode ser negativo.
III. Falso, pois m é Real e pode ser positivo.

21
03. Alternativa: A.
3
4
−
1
2
=
3 − 2
4
=
1
4
= 0,25
04. Alternativa: D.
Vamos chamar as retiradas de r, s e w: e de T o total de lâmpadas.
Precisamos calcular os múltiplos de 3, 5 e de 7, separando um múltiplo menor do que 100 que sirva
nas três equações abaixo:
De 3 em 3: 3 . r + 2 = Total
De 5 em 5: 5 . s + 2 = Total
De 7 em 7: 7 . w + 1 = Total
Primeiramente, vamos calcular o valor de w, sem que o total ultrapasse 100:
7 . 14 + 1 = 99, mas 3 . r + 2 = 99 vai dar que r = 32,333... (não convém)
7 . 13 + 1 = 92, e 3 . r + 2 = 92 vai dar r = 30 e 5 . s + 2 = 92 vai dar s = 18.
05. Alternativa: E.
Ida + volta = 7/5 . 1
3
4
. 𝑥 + 𝑥 =
7
5
5.3𝑥+ 20𝑥=7.4
20
15𝑥 + 20𝑥 = 28
35𝑥 = 28
𝑥 =
28
35
(: 7/7)
𝑥 =
4
5
(volta)
Ida:
3
4
.
4
5
=
3
5
06. Alternativa: C.
1 a 9 = 9 algarismos = 0,0019 = 0,009 ml
De 10 a 99, temos que saber quantos números tem.
99 – 10 + 1 = 90.
OBS: soma 1, pois quanto subtraímos exclui-se o primeiro número.
90 números de 2 algarismos: 0,00290 = 0,18ml
De 100 a 999
999 – 100 + 1 = 900 números
9000,003 = 2,7 ml
1000 = 0,004ml
Somando: 0,009 + 0,18 + 2,7 + 0,004 = 2,893
07. Alternativa: B.
Tarefa: x
Primeira semana: 3/8x
2 semana:
1
3
∙
3
8
𝑥 =
1
8
𝑥
1ª e 2ª semana:
3
8
𝑥 +
1
8
𝑥 =
4
8
𝑥 =
1
2
𝑥
Na 3ª e 4ª semana devem ser feito a outra metade.
3ªsemana: 2y
4ª semana: y
2𝑦 + 𝑦 =
1
2
𝑥
3𝑦 =
1
2
𝑥
𝑦 =
1
6
𝑥

22
08. Alternativa: B.
Tendo D = dividendo; d = divisor; Q = quociente e R = resto, podemos escrever essa divisão como:
D = d.Q + R
Sabemos que o R = 5
O divisor é o R + 3 → d = R + 3 = 5 + 3 = 8
E o quociente o dobro do divisor → Q = 2d = 2.8 = 16
Montando temos: D = 8.16 + 5 = 128 + 5 = 133.
09. Alternativa: B.
* número 40: é par.
40 / 2 + 17 = 20 + 17 = 37
* número 35: é ímpar.
Seu maior divisor é 35.
35 / 35 – 15 = 1 – 15 = – 14
* número 66: é par.
66 / 2 + 17 = 33 + 17 = 50
* número 27: é ímpar.
Seu maior divisor é 27.
27 / 27 – 15 = 1 – 15 = – 14
* Por fim, vamos somar os resultados:
37 – 14 + 50 – 14 = 87 – 28 = 59
10. Alternativa: B.
Vamos chamar o valor de cada cota de ( x ). Assim:
* Breno:
𝟏
𝟐
.
𝟏
𝟑
. 𝒙 = 𝟔𝟐𝟎𝟎𝟎
𝟏
𝟔
. 𝒙 = 𝟔𝟐𝟎𝟎𝟎
x = 62000 . 6
x = R$ 372000,00
* Carlos:
𝟏
𝟒
. 𝟑𝟕𝟐𝟎𝟎𝟎 = 𝑹$ 𝟗𝟑𝟎𝟎𝟎, 𝟎𝟎
ANÁLISE COMBINATÓRIA
A Análise Combinatória4
é a parte da Matemática que desenvolve meios para trabalharmos com
problemas de contagem, sendo eles:
- Princípio Fundamental da Contagem (PFC);
- Fatorial de um número natural;
- Tipos de Agrupamentos Simples (Arranjo, permutação e combinação);
- Tipos de Agrupamentos com Repetição (Arranjo, permutação e combinação).
A Análise Combinatória é o suporte da Teoria das Probabilidades, e de vital importância para as
ciências aplicadas, como a Medicina, a Engenharia, a Estatística entre outras.
Princípio Fundamental da Contagem-PFC (Princípio Multiplicativo)
O princípio multiplicativo ou fundamental da contagem constitui a ferramenta básica para resolver
problemas de contagem sem que seja necessário enumerar seus elementos, através das possibilidades
4
IEZZI, Gelson – Matemática – Volume Único
FILHO, Begnino Barreto; SILVA,Claudio Xavier da – Matemática – Volume Único - FTD
BOSQUILHA, Alessandra - Minimanual compacto de matemática: teoria e prática: ensino médio / Alessandra Bosquilha, Marlene Lima Pires Corrêa, Tânia Cristina
Neto G. Viveiro. -- 2. ed. rev. -- São Paulo: Rideel, 2003.

23
dadas. É uma das técnicas mais utilizadas para contagem, mas também dependendo da questão pode
se tornar trabalhosa.
Exemplos
1) Imagine que, na cantina de sua escola, existem cinco opções de suco de frutas: pêssego, maçã,
morango, caju e mamão. Você deseja escolher apenas um desses sucos, mas deverá decidir também se
o suco será produzido com água ou leite. Escolhendo apenas uma das frutas e apenas um dos
acompanhamentos, de quantas maneiras poderá pedir o suco?
2) Para ir da sua casa (cidade A) até a casa do seu amigo Pedro (que mora na cidade C) João precisa
pegar duas conduções: A1 ou A2 ou A3 que saem da sua cidade até a B e B1 ou B2 que o leva até o
destino final C. Vamos montar o diagrama da árvore para avaliarmos todas as possibilidades:
De forma resumida, e rápida podemos também montar através do princípio multiplicativo o número de
possibilidades:
3) De sua casa ao trabalho, Sílvia pode ir a pé, de ônibus ou de metrô. Do trabalho à faculdade, ela
pode ir de ônibus, metrô, trem ou pegar uma carona com um colega.
De quantos modos distintos Sílvia pode, no mesmo dia, ir de casa ao trabalho e de lá para a faculdade?
Vejamos, o trajeto é a junção de duas etapas:
1º) Casa → Trabalho: ao qual temos 3 possibilidades
2º) Trabalho → Faculdade: 4 possibilidades.

24
Multiplicando todas as possibilidades (pelo PFC), teremos: 3 x 4 = 12.
No total Sílvia tem 12 maneiras de fazer o trajeto casa – trabalho – faculdade.
DEFINIÇÃO do PFC: Se um evento que chamaremos de E1 puder ocorrer de a maneiras e um outro
evento que chamaremos de E2 puder ocorrer de b maneiras e E1 for independente de E2, assim a
quantidade de maneiras distintas de os dois eventos ocorrerem simultaneamente será dado por axb,
isto é, a quantidade de maneiras de a ocorrer, multiplicado pela quantidade de maneiras de b ocorrer.
Questões
01. (Pref. Chapecó/SC – Engenheiro de Trânsito – IOBV) Em um restaurante os clientes têm a sua
disposição, 6 tipos de carnes, 4 tipos de cereais, 4 tipos de sobremesas e 5 tipos de sucos. Se o cliente
quiser pedir 1 tipo carne, 1 tipo de cereal, 1 tipo de sobremesa e 1 tipo de suco, então o número de opções
diferentes com que ele poderia fazer o seu pedido, é:
(A) 19
(B) 480
(C) 420
(D) 90
02. (Pref. Rio de Janeiro/RJ – Agente de Administração – Pref. Rio de Janeiro) Seja N a
quantidade máxima de números inteiros de quatro algarismos distintos, maiores do que 4000, que podem
ser escritos utilizando-se apenas os algarismos 0, 1, 2, 3, 4, 5 e 6.
O valor de N é:
(A) 120
(B) 240
(C) 360
(D) 480
Comentários
01. Resposta: B.
A questão trata-se de princípio fundamental da contagem, logo vamos enumerar todas as
possibilidades de fazermos o pedido:
6 x 4 x 4 x 5 = 480 maneiras.
02. Resposta: C.
Pelo enunciado precisa ser um número maior que 4000, logo para o primeiro algarismo só podemos
usar os números 4,5 e 6 (3 possibilidades). Como se trata de números distintos para o segundo algarismo
poderemos usar os números (0,1,2,3 e também 4,5 e 6 dependo da primeira casa) logo teremos 7 – 1 =
6 possibilidades. Para o terceiro algarismos teremos 5 possibilidades e para o último, o quarto algarismo,
teremos 4 possibilidades, montando temos:
Basta multiplicarmos todas as possibilidades: 3 x 6 x 5 x 4 = 360.
Logo N é 360.
Fatorial de um Número Natural
É comum aparecerem produtos de fatores naturais sucessivos em problemas de análise combinatória,
tais como: 3. 2 . 1 ou 5. 4 . 3 . 2 . 1, por isso surgiu a necessidade de simplificarmos este tipo de notação,
facilitando os cálculos combinatórios. Assim, produtos em que os fatores chegam sucessivamente até a
unidade são chamados fatoriais.
Matematicamente:
Dado um número natural n, sendo n є N e n ≥ 2, temos:

25
Onde:
n! é o produto de todos os números naturais de 1 até n (lê-se: “n fatorial”)
Por convenção temos que:
Exemplos
1) De quantas maneiras podemos organizar 8 alunos em uma fila.
Observe que vamos utilizar a mesma quantidade de alunos na fila nas mais variadas posições:
Temos que 8! = 8.7.6.5.4.3.2.1 = 40320
2) Dado
9!
5!
, qual o valor dessa fração?
Observe que o denominador é menor que o numerador, então para que possamos resolver vamos
levar o numerador até o valor do denominador e simplificarmos:
Tipos de Agrupamento
Os agrupamentos que não possuem elementos repetidos, são chamamos de agrupamentos
simples. Dentre eles, temos aqueles onde a ordem é importante e os que a ordem não é importante.
Vamos ver detalhadamente cada um deles.
- Arranjo simples: agrupamentos simples de n elementos distintos tomados(agrupados) p a p. Aqui a
ordem dos seus elementos é importante, é o que diferencia.
Exemplos
1) Dados o conjunto S formado pelos números S= {1,2,3,4,5,6} quantos números de 3 algarismos
podemos formar com este conjunto?
Observe que 123 é diferente de 321 e assim sucessivamente, logo é um Arranjo.
Se fossemos montar todos os números levaríamos muito tempo, para facilitar os cálculos vamos utilizar
a fórmula do arranjo.
Pela definição temos: A n,p (Lê-se: arranjo de n elementos tomados p a p).
Então:
Utilizando a fórmula:

26
Onde n = 6 e p = 3
An, p =
n!
(n − p)!
→ A6,3 =
6!
(6 − 3)!
=
6!
3!
=
6.5.4.3!
3!
= 120
Então podemos formar com o conjunto S, 120 números com 3 algarismos.
2) Uma escola possui 18 professores. Entre eles, serão escolhidos: um diretor, um vice-diretor e um
coordenador pedagógico. Quantas as possibilidades de escolha?
n = 18 (professores)
p = 3 (cargos de diretor, vice-diretor e coordenador pedagógico)
An, p =
n!
(n − p)!
→ A18,3 =
18!
(18 − 3)!
=
18!
15!
=
18.17.16.15!
15!
= 4896 grupos
- Permutação simples: sequência ordenada de n elementos distintos (arranjo), ao qual utilizamos
todos os elementos disponíveis, diferenciando entre eles apenas a ordem. A permutação simples é um
caso particular do arranjo simples.
É muito comum vermos a utilização de permutações em anagramas (alterações da sequência das
letras de uma palavra).
Exemplos
1) Quantos anagramas podemos formar com a palavra CALO?
Utilizando a fórmula da permutação temos:
n = 4 (letras)
P4! = 4! = 4 . 3 . 2 . 1! = 24 . 1! (como sabemos 1! = 1) → 24 . 1 = 24 anagramas
2) Utilizando a palavra acima, quantos são os anagramas que começam com a letra L?
P3! = 3! = 3 . 2 . 1! = 6 anagramas que começam com a letra L.
- Combinação simples: agrupamento de n elementos distintos, tomados p a p, sendo p ≤ n. O que
diferencia a combinação do arranjo é que a ordem dos elementos não é importante.
Vemos muito o conceito de combinação quando queremos montar uma comitiva, ou quando temos
também de quantas maneiras podemos cumprimentar um grupo ou comitiva, entre outros.

27
Exemplos
1) Uma escola tem 7 professores de Matemática. Quatro deles deverão representar a escola em um
congresso. Quantos grupos de 4 professores são possíveis?
Observe que sendo 7 professores, se invertermos um deles de posição não alteramos o grupo formado,
os grupos formados são equivalentes. Para o exemplo acima temos ainda as seguintes possibilidades
que podemos considerar sendo como grupo equivalentes.
P1, P2, P4, P3 – P2, P1, P3, P4 – P3, P1, P2, P4 – P2, P4, P3, P4 – P4, P3, P1, P2 ...
Com isso percebemos que a ordem não é importante!
Vamos então utilizar a fórmula para agilizar nossos cálculos:
Aqui dividimos novamente por p, para desconsiderar todas as sequências repetidas (P1, P2, P3, P4 =
P4, P2, P1, P3= P3, P2, P4, P1=...).
Aplicando a fórmula:
Cn, p =
n!
(n − p)! p!
→ C7,4 =
7!
(7 − 4)! 4!
=
7!
3! 4!
=
7.6.5.4!
3! 4!
=
210
3.2.1
=
210
6
= 35 grupos de professores
2) Considerando dez pontos sobre uma circunferência, quantas cordas podem ser construídas com
extremidades em dois desses pontos?
Uma corda fica determinada quando escolhemos dois pontos entre
os dez.
Escolher (A,D) é o mesmo que escolher (D,A), então sabemos que
se trata de uma combinação.
Aqui temos então a combinação de 10 elementos tomados 2 a 2.
C10,2 =
n!
(n − p)! p!
=
10!
(10 − 2)! 2!
=
10!
8! 2!
=
10.9.8!
8! 2!
=
90
2
=
45 cordas
Agrupamentos com Repetição
Existem casos em que os elementos de um conjunto repetem-se para formar novos subconjuntos.
Nestes casos, devemos usar fórmulas de agrupamentos com repetição. Assim, teremos:
A) arranjo com repetição;
B) permutação com repetição;
C) combinação com repetição.
Vejamos:
a) Arranjo com repetição: ou arranjo completo, é um grupo de p elementos de um dado conjunto,
com n elementos distintos, onde a mudança de ordem determina grupos diferentes, podendo porém ter
elementos repetidos.
Indicamos por AR n,p

28
No arranjo com repetição, temos todos os elementos do conjunto à disposição a cada escolha, por
isso, pelo Princípio Fundamental da Contagem, temos:
Exemplo
Quantas chapas de automóvel compostas de 2 letras nas duas primeiras posições, seguidas por 4
algarismos nas demais posições (sendo 26 letras do nosso alfabeto e sendo os algarismos do sistema
decimal) podem ser formadas?
O número de pares de letras que poderá ser utilizado é:
Pois podemos repetir eles. Aplicando a fórmula de Arranjo com repetição temos:
𝑨𝑹 𝒏, 𝒑 = 𝒏𝒑
→ 𝑨𝑹 𝟐𝟔, 𝟐 = 𝟐𝟔𝟐
= 𝟔𝟕𝟔
Para a quantidade de números temos (0,1,2,3,4,5,6,7,8,9 – 10 algarismos):
→ 𝑨𝑹 𝟏𝟎, 𝟒 = 𝟏𝟎𝟒
= 𝟏𝟎. 𝟎𝟎𝟎
Assim o número de chapas que podemos ter é dado pela multiplicação dos valores achados:
676 . 10 000 = 6 760 000 possibilidades de placas.
Observação: Caso não pudesse ser utilizada a placa com a sequência de zeros, ou seja, com 4 zeros
teríamos:
→ 𝑨𝑹 𝟏𝟎, 𝟒 = 𝟔𝟕𝟔. 𝟏𝟎𝟒
− 𝟔𝟕𝟔. 𝟏 = 𝟔𝟕𝟔. (𝟏𝟎𝟎𝟎𝟎 − 𝟏)
b) Permutação com repetição: a diferença entre arranjo e permutação é que esta faz uso de todos
os elementos do conjunto. Na permutação com repetição, como o próprio nome indica, as repetições são
permitidas e podemos estabelecer uma fórmula que relacione o número de elementos, n, e as vezes em
que o mesmo elemento aparece.
Com α + β + γ + ... ≤ n
Exemplo
Quantos são os anagramas da palavra ARARA?
n = 5
α = 3 (temos 3 vezes a letra A)
β = 2 (temos 2 vezes a letra R)
Equacionando temos:

29
𝑷𝒏(∝,𝜷,𝜸,… )
=
𝒏!
𝜶! 𝜷! 𝜸!
… → 𝒑𝟓(𝟑,𝟐)
=
𝟓!
𝟑! 𝟐!
=
𝟓. 𝟒. 𝟑!
𝟑! 𝟐!
=
𝟓. 𝟒
𝟐. 𝟏
=
𝟐𝟎
𝟐
= 𝟏𝟎 𝒂𝒏𝒂𝒈𝒓𝒂𝒎𝒂𝒔
B.1) Permutação circular: a permutação circular com repetição pode ser generalizada através da
seguinte forma:
Vejamos o exemplo como chegar na fórmula, para aplicação.
- De quantas maneiras 5 meninas que brincam de roda podem formá-la?
Fazendo um esquema, observamos que são posições iguais:
O total de posições é 5! e cada 5 representa uma só permutação circular. Assim, o total de permutações
circulares será dado por:
𝑃𝑐5
=
5!
5
=
5.4!
5
= 4! = 4.3.2.1 = 24
C) Combinação com repetição: dado um conjunto com n elementos distintos, chama-se combinação
com repetição, classe p (ou combinação completa p a p) dos n elementos desse conjunto, a todo grupo
formado por p elementos, distintos ou não, em qualquer ordem.
Exemplo
Em uma combinação com repetição classe 2 do conjunto {a, b, c}, quantas combinações obtemos?
Ilustrando temos:
Utilizando a fórmula da combinação com repetição, verificamos o mesmo resultado sem necessidade
de enumerar todas as possibilidades:
n = 3 e p = 2
𝑪𝑹𝒏, 𝒑 = 𝑪 𝒏 + 𝒑 − 𝟏, 𝒑 → 𝑪𝑹 𝟑 + 𝟐 − 𝟏, 𝟐 → 𝑪𝑹𝟒, 𝟐 =
𝟒!
𝟐! (𝟒 − 𝟐)!
=
𝟒!
𝟐! 𝟐!
=
𝟒. 𝟑. 𝟐!
𝟐! 𝟐!
=
𝟏𝟐
𝟐
= 𝟔
Questões
01. (CRQ 2ª Região/MG – Auxiliar Administrativo – FUNDEP) Com 12 fiscais, deve-se fazer um
grupo de trabalho com 3 deles. Como esse grupo deverá ter um coordenador, que pode ser qualquer um
deles, o número de maneiras distintas possíveis de se fazer esse grupo é:
(A) 4
(B) 660
(C) 1 320
(D) 3 960

30
02. (PM/SP – Cabo – CETRO) Uma lei de certo país determinou que as placas das viaturas de polícia
deveriam ter 3 algarismos seguidos de 4 letras do alfabeto grego (24 letras). Sendo assim, o número de
placas diferentes será igual a
(A) 175.760.000.
(B) 183.617.280.
(C) 331.776.000.
(D) 358.800.000.
03. (TJ/RS – Técnico Judiciário - FAURGS) O Tribunal de Justiça está utilizando um código de leitura
de barras composto por 5 barras para identificar os pertences de uma determinada seção de trabalho. As
barras podem ser pretas ou brancas. Se não pode haver código com todas as barras da mesma cor, o
número de códigos diferentes que se pode obter é de
(A) 10.
(B) 30.
(C) 50.
(D) 150.
(E) 250.
04. (SEED/SP – Agente de Organização Escolar – VUNESP) Um restaurante possui pratos principais
e individuais. Cinco dos pratos são com peixe, 4 com carne vermelha, 3 com frango, e 4 apenas com
vegetais. Alberto, Bianca e Carolina pretendem fazer um pedido com três pratos principais individuais, um
para cada. Alberto não come carne vermelha nem frango, Bianca só come vegetais, e Carolina só não
come vegetais. O total de pedidos diferentes que podem ser feitos atendendo as restrições alimentares
dos três é igual a
(A) 384.
(B) 392.
(C) 396.
(D) 416.
(E)432.
05. (Pref. Jundiaí/SP – Eletricista – MAKIYAMA) Dentre os nove competidores de um campeonato
municipal de esportes radicais, somente os quatro primeiros colocados participaram do campeonato
estadual. Sendo assim, quantas combinações são possíveis de serem formadas com quatro desses nove
competidores?
(A) 126
(B)120
(C) 224
(D) 212
(E) 156
06. (Pref. Lagoa da Confusão/TO – Orientador Social – IDECAN) Renato é mais velho que Jorge
de forma que a razão entre o número de anagramas de seus nomes representa a diferença entre suas
idades. Se Jorge tem 20 anos, a idade de Renato é
(A) 24.
(B) 25.
(C) 26.
(D) 27.
(E) 28.
07. (Pref. Nepomuceno/MG – Técnico em Segurança do Trabalho – CONSULPLAN) Numa sala há
3 ventiladores de teto e 4 lâmpadas, todos com interruptores independentes. De quantas maneiras é
possível ventilar e iluminar essa sala mantendo, pelo menos, 2 ventiladores ligados e 3 lâmpadas acesas?
(A) 12.
(B) 18.
(C) 20.
(D) 24.
(E) 36.

31
08. (CREA/PR – Agente Administrativo– FUNDATEC) A fim de vistoriar a obra de um estádio de
futebol para a copa de 2014, um órgão público organizou uma comissão composta por 4 pessoas, sendo
um engenheiro e 3 técnicos.
Sabendo-se que em seu quadro de funcionários o órgão dispõe de 3 engenheiros e de 9 técnicos,
pode-se afirmar que a referida comissão poderá ser formada de _____ maneiras diferentes.
Assinale a alternativa que completa corretamente a lacuna do trecho acima.
(A) 252
(B) 250
(C) 243
(D) 127
(E) 81
09. (ESA – Música – EXÉRCITO BRASILEIRO) Colocando-se em ordem alfabética os anagramas da
palavra FUZIL, que posição ocupará o anagrama ZILUF.
(A) 103
(B) 104
(C) 105
(D) 106
(E) 107
10. (CODEMIG – Analista de Administração – Gestão de Concursos) Oito amigos encontraram-se
em uma festa. Se cada um dos amigos trocar um aperto de mão com cada um dos outros, quantos apertos
de mão serão trocados?
(A) 22.
(B) 25.
(C) 27.
(D) 28.
Comentários
01. Resposta: B
Esta questão trata-se de Combinação, pela fórmula temos:
Cn, p =
n!
(n − p)! p!
Onde n = 12 e p = 3
Cn, p =
n!
(n − p)! p!
→ C12,3 =
12!
(12 − 3)! 3!
=
12!
9! 3!
=
12.11.10.9!
9! 3!
=
1320
3.2.1
=
1320
6
= 220
Como cada um deles pode ser o coordenado, e no grupo tem 3 pessoas, logo temos 220 x 3 = 660.
02. Resposta: C
Algarismos possíveis: 0,1,2,3,4,5,6,7,8,9=10 algarismos
_ _ _ _ _ _ _
101010  242424 24=331.776.000
03. Resposta: B
_ _ _ _ _
22222=32 possibilidades se pudesse ser qualquer uma das cores
Mas, temos que tirar código todo preto e todo branco.
32-2=30
04. Resposta: E
Para Alberto:5+4=9
Para Bianca:4
Para Carolina: 12
_ _ _
9.4.12=432

32
05. Resposta: A
1001.
C_9,4 = 9! / 5!4! = (9∙8∙7∙6∙5!) / (5!∙24) = 126
06. Resposta: C
Anagramas de RENATO
_ _ _ _ _ _
6.5.4.3.2.1=720
Anagramas de JORGE
_ _ _ _ _
5.4.3.2.1=120
Razão dos anagramas:
720
120
= 6
Se Jorge tem 20 anos, Renato tem 20+6=26 anos
07. Resposta: C
1ª possibilidade:2 ventiladores e 3 lâmpadas
𝐶3,2 =
3!
1!2!
= 3
𝐶4,3 =
4!
1!3!
= 4
𝐶3,2 ∙ 𝐶4,3 = 3 ∙ 4 = 12
𝐶3,2 =
3!
1!2!
= 3
𝐶4,4 =
4!
0!4!
= 1
𝐶3,2 ∙ 𝐶4,4 = 3 ∙ 1 = 3
𝐶3,3 =
3!
0!3!
= 1
𝐶4,3 =
4!
1!3!
= 4
𝐶3,3 ∙ 𝐶4,3 = 1 ∙ 4 = 4
𝐶3,3 =
3!
0!3!
= 1
𝐶4,4 =
4!
0!4!
= 1
𝐶3,3 ∙ 𝐶4,4 = 1 ∙ 1 = 1
Somando as possibilidades: 12 + 3 + 4 + 1 = 20
08. Resposta: A
Engenheiros
𝐶3,1 =
3!
2! 1!
= 3
Técnicos
𝐶9,3 =
9!
3! 6!
=
9 ∙ 8 ∙ 7 ∙ 6!
6 ∙ 6!
= 84
3 . 84 = 252 maneiras

33
09. Resposta: D
O anagrama que ele quer é ZILUF, assim como se inicia com Z podemos admitir todos os outros
anagramas que iniciam com letra diferente de “Z” estão antes do desejado, assim:
F_ _ _ _ = 4.3.2.1 = 24
I_ _ _ _ = 4.3.2.1 = 24
L_ _ _ _ = 4.3.2.1 = 24
U_ _ _ _ = 4.3.2.1 = 24
Daí começa os com Z
Portanto colocaremos Z e a menor letra na segunda opção que será o F
ZF_ _ _ = 3.2.1 = 6
Agora depois do último que começa com ZF vem o que começa com ZI
Mas antes do L temos o F
Assim devemos contar todos que comecem por ZIF
ZIF_ _ = 2
Agora temos o que começa com ZIL
Mas só temos estes possíveis anagramas em ordem crescente que começam com ZIL
ZILFU = 1
ZILUF (Que é o anagrama que queremos)
Agora basta saber a posição em que ele ficará,
24 + 24 + 24 + 24 + 6 + 2 + 1 = 105 antes dele, portanto ele estará na 106ª posição.
10. Resposta: D
A primeira pessoa apertará a mão de 7
A Segunda, de 6, e assim por diante.
Portanto, haverá: 7+6+5+4+3+2+1=28
SISTEMA DE MEDIDAS
Sistema de Medidas Decimais: Área, volume, comprimento, capacidade, massa
Um sistema de medidas é um conjunto de unidades de medida que mantém algumas relações entre
si. O sistema métrico decimal é hoje o mais conhecido e usado no mundo todo. Na tabela seguinte,
listamos as unidades de medida de comprimento do sistema métrico. A unidade fundamental é o metro,
porque dele derivam as demais.
Há, de fato, unidades quase sem uso prático, mas elas têm uma função. Servem para que o sistema
tenha um padrão: cada unidade vale sempre 10 vezes a unidade menor seguinte.
Por isso, o sistema é chamado decimal.
E há mais um detalhe: embora o decímetro não seja útil na prática, o decímetro cúbico é muito usado
com o nome popular de litro.
As unidades de área do sistema métrico correspondem às unidades de comprimento da tabela anterior.
São elas: quilômetro quadrado (km2
), hectômetro quadrado (hm2
), etc. As mais usadas, na prática, são
o quilômetro quadrado, o metro quadrado e o hectômetro quadrado, este muito importante nas atividades
rurais com o nome de hectare (há): 1 hm2
= 1 ha.
2 - Sistema legal de medidas.

34
No caso das unidades de área, o padrão muda: uma unidade é 100 vezes a menor seguinte e não 10
vezes, como nos comprimentos. Entretanto, consideramos que o sistema continua decimal, porque 100
= 102
.
Existem outras unidades de medida mas que não pertencem ao sistema métrico decimal. Vejamos as
relações entre algumas essas unidades e as do sistema métrico decimal (valores aproximados):
1 polegada = 25 milímetros
1 milha = 1 609 metros
1 légua = 5 555 metros
1 pé = 30 centímetros
A nomenclatura é a mesma das unidades de comprimento acrescidas de quadrado.
Agora, vejamos as unidades de volume. De novo, temos a lista: quilômetro cúbico (km3
), hectômetro
cúbico (hm3
), etc. Na prática, são muitos usados o metro cúbico(m3
) e o centímetro cúbico(cm3
).
Nas unidades de volume, há um novo padrão: cada unidade vale 1000 vezes a unidade menor
seguinte. Como 1000 = 103
, o sistema continua sendo decimal.
A noção de capacidade relaciona-se com a de volume. Se o volume da água que enche um tanque é
de 7.000 litros, dizemos que essa é a capacidade do tanque. A unidade fundamental para medir
capacidade é o litro (l); 1l equivale a 1 dm3
e 1m³ = 1000l.
Cada unidade vale 10 vezes a unidade menor seguinte.
O sistema métrico decimal inclui ainda unidades de medidas de massa. A unidade fundamental é o
grama(g).
Nomenclatura:
Kg – Quilograma
hg – hectograma
dag – decagrama
g – grama
dg – decigrama

35
cg – centigrama
mg – miligrama
Dessas unidades, só têm uso prático o quilograma, o grama e o miligrama. No dia-a-dia, usa-se ainda
a tonelada (t).
Medidas Especiais:
1 Tonelada(t) = 1000 Kg
1 Arroba = 15 Kg
1 Quilate = 0,2 g
Relações entre unidades
Temos que:
1 kg = 1l = 1 dm3
1 hm2
= 1 ha = 10.000m2
1 m3
= 1000 l
Questões
01. (SESAP-RN – Administrador – COMPERVE/2018) Uma criança desenvolveu uma infecção cujo
tratamento deve ser feito com antibióticos. O antibiótico utilizado no tratamento tem recomendação diária
de 1,5 mg por um quilograma de massa corpórea, devendo ser administrado três vezes ao dia, em doses
iguais. Se a criança tem massa equivalente a 12 kg, cada dose administrada deve ser de
(A) 7,5 mg.
(B) 9,0 mg.
(C) 4,5 mg.
(D) 6,0 mg.
02. (MP/SP – Auxiliar de Promotoria I – Administrativo – VUNESP) O suco existente em uma jarra
preenchia
3
4
da sua capacidade total. Após o consumo de 495 mL, a quantidade de suco restante na jarra
passou a preencher
1
5
da sua capacidade total. Em seguida, foi adicionada certa quantidade de suco na
jarra, que ficou completamente cheia. Nessas condições, é correto afirmar que a quantidade de suco
adicionada foi igual, em mililitros, a
(A) 580.
(B) 720.
(C) 900.
(D) 660.
(E) 840.
03. (PM/SP – Oficial Administrativo – VUNESP) Em uma casa há um filtro de barro que contém, no
início da manhã, 4 litros de água. Desse filtro foram retirados 800 mL para o preparo da comida e meio
litro para consumo próprio. No início da tarde, foram colocados 700 mL de água dentro desse filtro e, até
o final do dia, mais 1,2 litros foram utilizados para consumo próprio. Em relação à quantidade de água
que havia no filtro no início da manhã, pode-se concluir que a água que restou dentro dele, no final do
dia, corresponde a uma porcentagem de
(A) 60%.
(B) 55%.
(C) 50%.
(D) 45%.
(E) 40%.

36
04. (UFPE – Assistente em Administração – COVEST) Admita que cada pessoa use, semanalmente,
4 bolsas plásticas para embrulhar suas compras, e que cada bolsa é composta de 3 g de plástico. Em um
país com 200 milhões de pessoas, quanto plástico será utilizado pela população em um ano, para
embrulhar suas compras? Dado: admita que o ano é formado por 52 semanas. Indique o valor mais
próximo do obtido.
(A) 108
toneladas
(B) 107
toneladas
(C) 106
toneladas
(D) 105
toneladas
(E) 104
toneladas
05. (PM/SP – Oficial Administrativo – VUNESP) Uma chapa de alumínio com 1,3 m2
de área será
totalmente recortada em pedaços, cada um deles com 25 cm2
de área. Supondo que não ocorra nenhuma
perda durante os cortes, o número de pedaços obtidos com 25 cm2
de área cada um, será:
(A) 52000.
(B) 5200.
(C) 520.
(D) 52.
(E) 5,2.
06. (CLIN/RJ - Gari e Operador de Roçadeira - COSEAC) Uma peça de um determinado tecido tem
30 metros, e para se confeccionar uma camisa desse tecido são necessários 15 decímetros. Com duas
peças desse tecido é possível serem confeccionadas:
(A) 10 camisas
(B) 20 camisas
(C) 40 camisas
(D) 80 camisas
07. (CLIN/RJ - Gari e Operador de Roçadeira - COSEAC) Um veículo tem capacidade para
transportar duas toneladas de carga. Se a carga a ser transportada é de caixas que pesam 4 quilogramas
cada uma, o veículo tem capacidade de transportar no máximo:
(A) 50 caixas
(B) 100 caixas
(C) 500 caixas
(D) 1000 caixas
08. (PM/SP – Oficial Administrativo – VUNESP) Um trecho de uma estrada com 5,6 km de
comprimento está sendo reparado. A empresa A, responsável pelo serviço, já concluiu
3
7
do total a ser
reparado e, por motivos técnicos,
2
5
do trecho que ainda faltam reparar serão feitos por uma empresa B.
O número total de metros que a empresa A ainda terá que reparar é
(A) 1920.
(B) 1980.
(C) 2070.
(D) 2150.
(E) 2230.
Comentários
01. Resposta: D
Observe que 1,5mg é a dose diária para cada quilograma da criança, como ele é aplicado 3x ao dia,
teremos 0,5mg por aplicação, a criança possui 12kg, assim a quantidade de remédio por aplicação será
de:
0,5 . 12 = 6,0mg
02. Resposta: B.
Vamos chamar de x a capacidade total da jarra. Assim:
3
4
. 𝑥 − 495 =
1
5
. 𝑥

37
3
4
. 𝑥 −
1
5
. 𝑥 = 495
5.3.𝑥 − 4.𝑥=20.495
20
15x – 4x = 9900
11x = 9900
x = 9900 / 11
x = 900 mL (capacidade total)
Como havia 1/5 do total (1/5 . 900 = 180 mL), a quantidade adicionada foi de 900 – 180 = 720 mL
03. Resposta: B.
4 litros = 4000 ml; 1,2 litros = 1200 ml; meio litro = 500 ml
4000 – 800 – 500 + 700 – 1200 = 2200 ml (final do dia)
Utilizaremos uma regra de três simples:
ml %
4000 ------- 100
2200 ------- x
4000.x = 2200 . 100 x = 220000 / 4000 = 55%
04. Resposta: D.
4 . 3 . 200000000 . 52 = 1,248 . 1011
g = 1,248 . 105
t
05. Resposta: C.
1,3 m2
= 13000 cm2
13000 / 25 = 520 pedaços
06. Resposta: C.
Como eu quero 2 peças desse tecido e 1 peça possui 30 metros logo:
30 . 2 = 60 m. Temos que trabalhar com todas na mesma unidade: 1 m é 10dm assim temos 60m . 10
= 600 dm, como cada camisa gasta um total de 15 dm, temos então:
600/15 = 40 camisas.
07. Resposta: C.
Uma tonelada(ton) é 1000 kg, logo 2 ton. 1000kg= 2000 kg
Cada caixa pesa 4kg  2000 kg/ 4kg = 500 caixas.
08. Resposta: A.
Primeiramente, vamos transformar Km em metros: 5,6 Km = 5600 m (.1000)
Faltam
7
7
−
3
7
=
4
7
do total, ou seja,
4
7
𝑑𝑒 5600 =
4.5600
7
= 3200𝑚
A empresa B vai reparar
2
5
𝑑𝑒 3200 =
2.3200
5
= 1280𝑚
Então, a empresa A vai reparar 3200 – 1280 = 1920m
SISTEMA DE MEDIDAS NÃO DECIMAIS (TEMPO E ÂNGULO)
Antigamente, para saber o melhor momento de caçar e plantar, entre outras atividades, as civilizações
observavam a natureza, ou seja, utilizavam-se de fenômenos naturais periódicos.
A unidade básica para a contagem do tempo é o dia, que corresponde ao período de tempo entre dois
eventos equivalentes sucessivos: por exemplo, o intervalo de tempo entre duas ocorrências do nascer do
Sol, que corresponde, em média (dia solar médio), a 24 horas.
O ano solar é o período de tempo decorrido para completar um ciclo de estações (primavera, verão,
outono e inverno). O ano solar médio tem a duração de aproximadamente 365 dias, 5 horas, 48 minutos
e 47 segundos (365,2422 dias). Também é conhecido como ano trópico. A cada quatro anos, as horas
extras acumuladas são reunidas no dia 29 de fevereiro, formando o ano bissexto, ou seja, o ano com 366
dias.
Temos uma maneira prática de verificar se um ano é bissexto:
- Se o número que indica o ano é terminado em 00, esse ano será bissexto se o número for divisível
por 400.

38
- Se o número que indica o ano não é terminado em 00, esse ano será bissexto se o número for divisível
por 4.
Exemplo:
O ano de 2000, por exemplo, foi bissexto porque 2000 termina em 00 e é divisível por 400.
Os calendários antigos baseavam-se em meses lunares (calendários lunares) ou no ano solar
(calendário solar) para contagem do tempo. Eles ainda podem definir outras unidades de tempo, como a
semana, para o propósito de planejar atividades regulares que não se encaixam facilmente com meses
ou anos.
O Ano é dividido em 12 meses, os meses, em semanas, e cada semana, em 7 dias.
O período de 2 meses corresponde a um bimestre, o de 3 meses a um trimestre e o de 6 meses, a um
semestre.
Concluindo:
- 1 ano tem 365 a 366(bissexto) dias;
- 1 ano está dividido em 12 meses;
- 1 mês tem de 30 a 31 dias;
- 1 dia tem 24 horas
Para medirmos o tempo durante o dia, utilizamos o relógio, que pode ser de ponteiros ou digital.
Em geral, os relógios marcam as HORAS, os MINUTOS e os SEGUNDOS.
- 1 dia tem 24 horas.
- 1 hora tem 60 minutos.
- 1 minuto tem 60 segundos.
Observe-se que não é correto escrever 3,20 horas como forma de representar 3h20min, pois o sistema
de medida de tempo não é decimal. O 0,20h representa 12 minutos, pois 0,20.60 min = 12, logo 3,20h =
3horas 12 minutos.
- Adição e Subtração de Medida de tempo
Ao adicionarmos ou subtrairmos medidas de tempo, precisamos estar atentos as unidades. Vejamos
os exemplos:
A) 1 h 50 min + 30 min
Observe que ao somar 50 + 30, obtemos 80 minutos, como sabemos que 1 hora tem 60 minutos,
temos, então acrescentamos a hora +1, e subtraímos 80 – 60 = 20 minutos, é o que resta nos minutos:

39
Logo o valor encontrado é de 2 h 20 min.
B) 2 h 20 min – 1 h 30 min
Observe que não podemos subtrair 20 min de 30 min, então devemos passar uma hora (+1) dos 2 para
a coluna minutos.
Então teremos novos valores para fazermos nossa subtração, 20 + 60 = 80:
Logo o valor encontrado é de 50 min.
Medidas de Ângulos e suas
Transformações
Para medir ângulos, também temos um sistema não decimal. Nesse caso, a unidade básica é o grau.
Na astronomia, na cartografia e na navegação são necessárias medidas inferiores a 1º. Temos, então:
1 grau equivale a 60 minutos (1º = 60’)
1 minuto equivale a 60 segundos (1’ = 60”)
Os minutos e os segundos dos ângulos não são, é claro, os mesmos do sistema de tempo – hora,
minuto e segundo. Há uma coincidência de nomes, mas até os símbolos que os indicam são diferentes:
1h 32min 24s é um intervalo de tempo ou um instante do dia.
1º 32’ 24” é a medida de um ângulo.
Por motivos óbvios, cálculos no sistema hora – minuto – segundo são similares a cálculos no sistema
grau – minuto – segundo, embora esses sistemas correspondam a grandezas distintas.
Questões
01. (SESAP – RN – Técnico em Enfermagem – COMPERVE/2018) Uma profissional de enfermagem
deve administrar 250 ml de soro fisiológico em um paciente durante 90 minutos. Para obter a vazão
correta do soro em gotas por minuto, ela deverá utilizar a fórmula de gotejamento, dividindo o volume do
soro em mililitros pelo triplo do tempo em horas. De acordo com essa fórmula, a quantidade de gotas por
minuto dever ser de, aproximadamente,

40
(A) 28.
(B) 42.
(C) 56.
(D) 70.
02. (Pref. Camaçari/BA – Téc. Vigilância Em Saúde NM – AOCP) Joana levou 3 horas e 53 minutos
para resolver uma prova de concurso, já Ana levou 2 horas e 25 minutos para resolver a mesma prova.
Comparando o tempo das duas candidatas, qual foi a diferença encontrada?
(A) 67 minutos.
(B) 75 minutos.
(C) 88 minutos.
(D) 91 minutos.
(E) 94 minutos.
03. (SAAE/SP – Auxiliar de Manutenção Geral – VUNESP) A tabela a seguir mostra o tempo,
aproximado, que um professor leva para elaborar cada questão de matemática.
O gráfico a seguir mostra o número de questões de matemática que ele elaborou.
O tempo, aproximado, gasto na elaboração dessas questões foi
(A) 4h e 48min.
(B) 5h e 12min.
(C) 5h e 28min.
(D) 5h e 42min.
(E) 6h e 08min.
04. (CEFET – Auxiliar em Administração – CESGRANRIO) Para obter um bom acabamento, um
pintor precisa dar duas demãos de tinta em cada parede que pinta. Sr. Luís utiliza uma tinta de secagem
rápida, que permite que a segunda demão seja aplicada 50 minutos após a primeira. Ao terminar a
aplicação da primeira demão nas paredes de uma sala, Sr. Luís pensou: “a segunda demão poderá ser
aplicada a partir das 15h 40min.”
Se a aplicação da primeira demão demorou 2 horas e 15 minutos, que horas eram quando Sr. Luís
iniciou o serviço?
(A) 12h 25 min
(B) 12h 35 min
(C) 12h 45 min
(D) 13h 15 min
(E) 13h 25 min

41
Comentários
01. Resposta: C.
Para resolver esta questão temos que estar atentos ao enunciado, pois é dividir a quantidade em ml
pelo tempo em horas, então 90min = 1,5hora.
Logo, 250 : 4,5 = 55,555... que é aproximadamente 56.
02. Resposta: C.
Como 1h tem 60 minutos.
Então a diferença entre as duas é de 60+28=88 minutos.
03. Resposta: D.
T = 8 . 4 + 10 . 6 + 15 . 10 + 20 . 5 =
= 32 + 60 + 150 + 100 = 342 min
Fazendo: 342 / 60 = 5 h, com 42 min (resto)
04. Resposta: B.
15 h 40 – 2 h 15 – 50 min = 12 h 35min
RAZÃO
Razão5
é o quociente (divisão) entre dois números (quantidades, medidas, grandezas).
𝑎
𝑏
𝑜𝑢 𝑎: 𝑏 , 𝑐𝑜𝑚 𝑏 ≠ 0
Onde:
Você tem que ficar atento ao fato da frase que estiver o contexto, pois depende da ordem em que for
expressa.
Exemplos
01. Em um vestibular para o curso de marketing, participaram 3600 candidatos para 150 vagas. A
razão entre o número de vagas e o número de candidatos, nessa ordem, foi de
𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑣𝑎𝑔𝑎𝑠
𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑐𝑎𝑛𝑑𝑖𝑑𝑎𝑡𝑜𝑠
=
150
3600
=
1
24
Lemos a fração como: Um vinte e quatro avos ( pronuncia-se “ávos”).
02. Em um processo seletivo diferenciado, os candidatos obtiveram os seguintes resultados:
− Alana resolveu 11 testes e acertou 5
− Beatriz resolveu 14 testes e acertou 6
− Cristiane resolveu 15 testes e acertou 7
5
IEZZI, Gelson – Fundamentos da Matemática – Vol. 11 – Financeira e Estatística Descritiva
IEZZI, Gelson – Matemática Volume Único
http://educacao.globo.com
3 - Razões e proporções; divisão proporcional; regras de três simples e
compostas; porcentagens.

42
− Daniel resolveu 17 testes e acertou 8
− Edson resolveu 21 testes e acertou 9
O candidato contratado, de melhor desempenho, (razão de acertos para número de testes), foi:
𝐴𝑙𝑎𝑛𝑎:
5
11
= 0,45
𝐵𝑒𝑎𝑡𝑟𝑖𝑧:
6
14
= 0,42
𝐶𝑟𝑖𝑠𝑡𝑖𝑎𝑛𝑒:
7
15
= 0,46
𝐷𝑎𝑛𝑖𝑒𝑙:
8
17
= 0,47
𝐸𝑑𝑠𝑜𝑛:
9
21
= 0,42
Daniel teve o melhor desempenho pois 0,47 foi o maior número.
- Quando a e b forem medidas de uma mesma grandeza, essas devem ser expressas na mesma
unidade.
Razões Especiais
Escala
Muitas vezes precisamos ilustrar distâncias muito grandes de forma reduzida, então utilizamos a
escala, que é a razão da medida no mapa com a medida real (ambas na mesma unidade).
𝐸 =
𝑚𝑒𝑑𝑖𝑑𝑎 𝑛𝑜 𝑚𝑎𝑝𝑎
𝑚𝑒𝑑𝑖𝑑𝑎 𝑟𝑒𝑎𝑙
Velocidade Média
É a razão entre a distância percorrida e o tempo total de percurso. As unidades utilizadas são km/h,
m/s, entre outras.
𝑉 =
𝑑𝑖𝑠𝑡â𝑛𝑐𝑖𝑎 𝑝𝑒𝑐𝑜𝑟𝑟𝑖𝑑𝑎
𝑡𝑒𝑚𝑝𝑜 𝑡𝑜𝑡𝑎𝑙
Densidade
É a razão entre a massa de um corpo e o seu volume. As unidades utilizadas são g/cm³, kg/m³, entre
outras.
𝐷 =
𝑚𝑎𝑠𝑠𝑎 𝑑𝑜 𝑐𝑜𝑟𝑝𝑜
𝑣𝑜𝑙𝑢𝑚𝑒 𝑑𝑜 𝑐𝑜𝑟𝑝𝑜
PROPORÇÃO
É uma igualdade entre duas razões.
Dada as razões
𝑎
𝑏
e
𝑐
𝑑
, à setença de igualdade
𝑎
𝑏
=
𝑐
𝑑
chama-se proporção6
.
Onde:
Exemplo
1 - O passageiro ao lado do motorista observa o painel do veículo e vai anotando, minuto a minuto, a
distância percorrida. Sua anotação pode ser visualizada na tabela a seguir:
6
IEZZI, Gelson – Fundamentos da Matemática – Vol. 11 – Financeira e Estatística Descritiva
http://educacao.globo.com

43
Distância percorrida (em km) 2 4 6 8 ...
Tempo gasto (em min) 1 2 3 4 ...
Nota-se que a razão entre a distância percorrida e o tempo gasto para percorrê-la é sempre igual a 2:
2
1
= 2 ;
4
2
= 2 ;
6
3
= 2 ;
8
4
= 2
Então:
2
1
=
4
2
=
6
3
=
8
4
Dizemos que os números da sucessão (2,4,6, 8, ...) são diretamente proporcionais aos números da
sucessão (1,2,3,3, 4, ...).
Propriedades da Proporção
1 - Propriedade Fundamental
O produto dos meios é igual ao produto dos extremos, isto é, a. d = b. c
Exemplo
Na proporção
45
30
=
9
6
,(lê-se: “45 está para 30, assim como 9 está para 6.), aplicando a propriedade
fundamental, temos: 45.6 = 30.9 = 270
2 - A soma dos dois primeiros termos está para o primeiro (ou para o segundo termo), assim como a
soma dos dois últimos está para o terceiro (ou para o quarto termo).
𝑎
𝑏
=
𝑐
𝑑
→
𝑎 + 𝑏
𝑎
=
𝑐 + 𝑑
𝑐
𝑜𝑢
𝑎 + 𝑏
𝑏
=
𝑐 + 𝑑
𝑑
Exemplo
2
3
=
6
9
→
2 + 3
2
=
6 + 9
6
→
5
2
=
15
6
= 30 𝑜𝑢
2 + 3
3
=
6 + 9
9
→
5
3
=
15
9
= 45
3 - A diferença entre os dois primeiros termos está para o primeiro (ou para o segundo termo), assim
como a diferença entre os dois últimos está para o terceiro (ou para o quarto termo).
𝑎
𝑏
=
𝑐
𝑑
→
𝑎 − 𝑏
𝑎
=
𝑐 − 𝑑
𝑐
𝑜𝑢
𝑎 − 𝑏
𝑏
=
𝑐 − 𝑑
𝑑
Exemplo
2
3
=
6
9
→
2 − 3
2
=
6 − 9
6
→
−1
2
=
−3
6
= −6 𝑜𝑢
2 − 3
3
=
6 − 9
9
→
−1
3
=
−3
9
= −9
4 - A soma dos antecedentes está para a soma dos consequentes, assim como cada antecedente está
para o seu consequente.
𝑎
𝑏
=
𝑐
𝑑
→
𝑎 + 𝑐
𝑏 + 𝑑
=
𝑎
𝑏
𝑜𝑢
𝑎 + 𝑐
𝑏 + 𝑑
=
𝑐
𝑑
Exemplo
2
3
=
6
9
→
2 + 6
3 + 9
=
2
3
→
8
12
=
2
3
= 24 𝑜𝑢
2 + 6
3 + 9
=
6
9
→
8
12
=
6
9
= 72

44
5 - A diferença dos antecedentes está para a diferença dos consequentes, assim como cada
antecedente está para o seu consequente.
𝑎
𝑏
=
𝑐
𝑑
→
𝑎 − 𝑐
𝑏 − 𝑑
=
𝑎
𝑏
𝑜𝑢
𝑎 − 𝑐
𝑏 − 𝑑
=
𝑐
𝑑
Exemplo
6
9
=
2
3
→
6 − 2
9 − 3
=
6
9
→
4
6
=
6
9
= 36 𝑜𝑢
6 − 2
9 − 3
=
2
3
→
4
6
=
2
3
= 12
Problemas envolvendo razão e proporção
01. Em uma fundação, verificou-se que a razão entre o número de atendimentos a usuários internos e
o número de atendimento total aos usuários (internos e externos), em um determinado dia, nessa ordem,
foi de 3/5. Sabendo que o número de usuários externos atendidos foi 140, pode-se concluir que, no total,
o número de usuários atendidos foi:
A) 84
B) 100
C) 217
D) 280
E) 350
Resolução:
Usuários internos: i
Usuários externos: e
Sabemos que neste dia foram atendidos 140 externos → e = 140
𝑖
𝑖+𝑒
=
3
5
=
𝑖
𝑖+140
, usando o produto dos meios pelos extremos temos
5i = 3(i + 140) → 5i = 3i + 420 → 5i – 3i = 420 → 2i = 420 → i =
420
2
→ i = 210
i + e = 210 + 140 = 350
Resposta “E”
02. Em um concurso participaram 3000 pessoas e foram aprovadas 1800. A razão do número de
candidatos aprovados para o total de candidatos participantes do concurso é:
A) 2/3
B) 3/5
C) 5/10
D) 2/7
E) 6/7
Resolução:
Resposta “B”
03. Em um dia de muita chuva e trânsito caótico, 2/5 dos alunos de certa escola chegaram atrasados,
sendo que 1/4 dos atrasados tiveram mais de 30 minutos de atraso. Sabendo que todos os demais alunos
chegaram no horário, pode-se afirmar que nesse dia, nessa escola, a razão entre o número de alunos
que chegaram com mais de 30 minutos de atraso e número de alunos que chegaram no horário, nessa
ordem, foi de:
A) 2:3
B) 1:3
C) 1:6
D) 3:4
E) 2:5
Resolução:

45
Se
2
5
chegaram atrasados
1 −
2
5
=
3
5
𝑐ℎ𝑒𝑔𝑎𝑟𝑎𝑚 𝑛𝑜 ℎ𝑜𝑟á𝑟𝑖𝑜
2
5
∙
1
4
=
1
10
𝑡𝑖𝑣𝑒𝑟𝑎𝑚 𝑚𝑎𝑖𝑠 𝑑𝑒 30 𝑚𝑖𝑛𝑢𝑡𝑜𝑠 𝑑𝑒 𝑎𝑡𝑟𝑎𝑠𝑜
𝑟𝑎𝑧ã𝑜 =
𝑡𝑖𝑣𝑒𝑟𝑎𝑚 𝑚𝑎𝑖𝑠 𝑑𝑒 30 min 𝑑𝑒 𝑎𝑡𝑟𝑎𝑠𝑜
𝑐ℎ𝑒𝑔𝑎𝑟𝑎𝑚 𝑛𝑜 ℎ𝑜𝑟á𝑟𝑖𝑜
=
1
10
3
5
𝑟𝑎𝑧ã𝑜 =
1
10
∙
5
3
=
1
6
𝑜𝑢 1: 6
Resposta “C”
Questões
01. (Pref. de Cerquilho/SP – Professor de Ensino Fundamental I – Metro Capital Soluções/2018)
Durante um campeonato de tiro ao alvo, José disparou 12 vezes. Sabendo que a razão do número de
acertos para o total de disparos foi de 3/4 (três quartos), quantos disparos José acertou?
(A) 7.
(B) 10.
(C) 4.
(D) 7.
(E) 9.
02. (Colégio Pedro II – Professor – Colégio Pedro II/2018) O trabalho infantil é um dos mais graves
problemas do país.
De acordo com a Pesquisa Nacional de Amostra por Domicílio (PNAD 2015), mais de 2,7 milhões de
crianças e adolescentes, de 5 a 17 anos, estão em situação de trabalho no Brasil – no mundo, são 152
milhões que estão no trabalho precoce.
Disponível em: http://www.chegadetrabalhoinfantil.org.br. Acesso em: 30 jul. 2018
De acordo com os dados apresentados, a fração que representa o número de meninas em situação
de trabalho infantil no Brasil é:
(A) 2/3
(B) 5/10
(C) 9/27
(D) 94/100
03. (FUNCABES – Escriturário – PROMUN/2018) Em um concurso público em que participaram 3000
candidatos, 1800 foram aprovados. A razão do número de candidatos aprovados para o total de
candidatos participantes do concurso é:
(A) 2/3
(B) 3/5
(C) 5/10
(D) 2/7

46
04. (MPE/SP – Oficial de Promotoria – VUNESP) Alfredo irá doar seus livros para três bibliotecas da
universidade na qual estudou. Para a biblioteca de matemática, ele doará três quartos dos livros, para a
biblioteca de física, um terço dos livros restantes, e para a biblioteca de química, 36 livros. O número de
livros doados para a biblioteca de física será
(A) 16.
(B) 22.
(C) 20.
(D) 24.
(E)18.
05. (EBSERH/HUPA – Técnico em Informática – IDECAN) Entre as denominadas razões especiais
encontram-se assuntos como densidade demográfica, velocidade média, entre outros. Supondo que a
distância entre Rio de Janeiro e São Paulo seja de 430 km e que um ônibus, fretado para uma excursão,
tenha feito este percurso em 5 horas e 30 minutos. Qual foi a velocidade média do ônibus durante este
trajeto, aproximadamente, em km/h?
(A) 71 km/h
(B) 76 km/h
(C) 78 km/h
(D) 81 km/h
(E) 86 km/h.
06. (SEPLAN/GO – Perito Criminal – FUNIVERSA) Em uma ação policial, foram apreendidos 1
traficante e 150 kg de um produto parecido com maconha. Na análise laboratorial, o perito constatou que
o produto apreendido não era maconha pura, isto é, era uma mistura da Cannabis sativa com outras
ervas. Interrogado, o traficante revelou que, na produção de 5 kg desse produto, ele usava apenas 2 kg
da Cannabis sativa; o restante era composto por várias “outras ervas”. Nesse caso, é correto afirmar que,
para fabricar todo o produto apreendido, o traficante usou
(A) 50 kg de Cannabis sativa e 100 kg de outras ervas.
(B) 55 kg de Cannabis sativa e 95 kg de outras ervas.
(C) 60 kg de Cannabis sativa e 90 kg de outras ervas.
(D) 65 kg de Cannabis sativa e 85 kg de outras ervas.
(E) 70 kg de Cannabis sativa e 80 kg de outras ervas.
07. (Pref. Maranguape/CE – Prof. de Educação Básica – GR Consultoria e Assessoria) Eu tenho
duas réguas, uma que ao quebrar ficou com 24 cm de comprimento e a outra tem 30 cm, portanto, a
régua menor é quantos por cento da régua maior?
(A) 90%
(B) 75%
(C) 80%
(D) 85%
08. (SAAE/SP – Auxiliar de Manutenção Geral – VUNESP) Uma cidade A, com 120 km de vias,
apresentava, pela manhã, 51 km de vias congestionadas. O número de quilômetros de vias
congestionadas numa cidade B, que tem 280 km de vias e mantém a mesma proporção que na cidade A,
é
(A) 119 km.
(B) 121 km.
(C) 123 km.
(D) 125 km.
(E) 127 km.
09. (FINEP – Assistente – CESGRANRIO) Maria tinha 450 ml de tinta vermelha e 750 ml de tinta
branca. Para fazer tinta rosa, ela misturou certa quantidade de tinta branca com os 450 ml de tinta
vermelha na proporção de duas partes de tinta vermelha para três partes de tinta branca.
Feita a mistura, quantos ml de tinta branca sobraram?
(A) 75
(B) 125
(C) 175
(D) 375

47
(E) 675
10. (MP/SP – Auxiliar de Promotoria I – VUNESP) A medida do comprimento de um salão retangular
está para a medida de sua largura assim como 4 está para 3. No piso desse salão, foram colocados
somente ladrilhos quadrados inteiros, revestindo-o totalmente. Se cada fileira de ladrilhos, no sentido do
comprimento do piso, recebeu 28 ladrilhos, então o número mínimo de ladrilhos necessários para revestir
totalmente esse piso foi igual a
(A) 588.
(B) 350.
(C) 454.
(D) 476.
(E) 382.
Comentários
01. Resposta: E
A razão do número de acertos para o total é de
3
4
e o total de disparos foi 12, assim a proporção fica
da seguinte forma:
3
4
=
𝑥
12
4x = 3.12
4x = 36
x =
36
4
x = 9
02. Resposta: C
Vamos resolver este pela forma mais simples, nos dados apresentados temos que 2 em cada 3
crianças em situação de trabalho infantil são do sexo masculino, assim sobra apenas 1 em cada 3 para
o sexo feminino, em fração seria
1
3
, mas não temos esta resposta, porém temos
9
27
que nada mais é que
1
3
porém não está simplificado, assim
1
3
=
9
27
.
03. Resposta: B
De acordo com a ordem que foi expressa devemos ter 1800 no numerador e 3000 será o denominador,
ficando assim:
1800
3000
, simplificando:
18
30
=
3
5
04. Resposta: E
X = total de livros
Matemática = ¾ x, restou ¼ de x
Física =
1
3
.
1
4
= 1/12
Química = 36 livros
Logo o número de livros é:
3𝑥
4
+
1𝑥
12
+ 36 = x
Fazendo o m.m.c. dos denominadores (4,12) = 12
Logo:
9𝑥 + 1𝑥 + 432 = 12𝑥
12
→ 10𝑥 + 432 = 12𝑥 → 12𝑥 − 10𝑥 = 432 → 2𝑥 = 432 → 𝑥 =
432
2
→ 𝑥 = 216
Como a Biblioteca de Física ficou com 1/12x, logo teremos:
1
12
. 216 =
216
12
= 18
05. Resposta: C
5h30min = 5,5h, transformando tudo em hora e suas frações.
430
5,5
= 78,18 𝑘𝑚/ℎ

48
06. Resposta: C
O enunciado fornece que a cada 5kg do produto temos que 2kg da Cannabis sativa e os demais outras
ervas. Podemos escrever em forma de razão
2
5
, logo:
2
5
. 150 = 60𝑘𝑔 𝑑𝑒 𝐶𝑎𝑛𝑛𝑎𝑏𝑖𝑠 𝑠𝑎𝑡𝑖𝑣𝑎 ∴ 150 − 60 = 90𝑘𝑔 𝑑𝑒 𝑜𝑢𝑡𝑟𝑎𝑠 𝑒𝑟𝑣𝑎𝑠
07. Resposta: C
Como é a razão do menor pelo maior temos: 24/30 = 0,80. 100 = 80%
08. Resposta: A
A razão da cidade A será:
51
120
A da cidade B será:
𝑐𝑜𝑛𝑔𝑒𝑠𝑡𝑖𝑜𝑛𝑎𝑑𝑎𝑠
280
Como seguem a mesma proporção teremos a seguinte proporção:
51
120
=
𝑥
280
120.x = 51. 280 → x = 14280 / 120 → x = 119 km
09. Resposta: A
Como temos duas partes de tinta vermelha para três partes de tinta branca a fração ficará
2
3
temos
ainda que ela utilizou 450ml de tinta vermelha, então vamos encontrar o quanto ela utilizou de tinta branca
e depois descobrir o quanto sobrou do total (750ml)
2
3
=
450
𝑥
2x = 450. 3 → x = 1350 / 2 → x = 675 ml de tinta branca foram utilizadas.
Sobraram: 750 ml – 675 ml = 75 ml
10. Resposta: A
Chamando de C o comprimento e de L a largura, teremos a seguinte proporção
𝐶
𝐿
=
4
3
Como no comprimento foram utilizados 28 ladrilhos, teremos C = 28 e substituindo na proporção, ficará:
28
𝐿
=
4
3
4L = 28. 3
L =
84
4
L = 21 ladrilhos
Como teremos 28 ladrilhos no comprimento e 21 na largura, a quantidade total será dada pela área
dessa região retangular, ou seja, o produto do comprimento pela largura.
Assim, o total de ladrilhos foi de 28. 21 = 588.
DIVISÃO PROPORCIONAL
Uma forma de divisão no qual determinam-se valores (a,b,c,..) que, divididos por quocientes (x,y,z..)
previamente determinados, mantêm-se uma razão que não tem variação, também é conhecida como
regra de sociedade.
Divisão Diretamente Proporcional
Divisão em duas partes diretamente proporcionais
Para decompor um número M em duas partes A e B diretamente proporcionais a p e q, montamos um
sistema com duas equações e duas incógnitas, de modo que a soma das partes seja A + B = M, porém

49
𝐴
𝑝
=
𝐵
𝑞
A solução segue de acordo com as propriedades das proporções:
𝐴
𝑝
=
𝐵
𝑞
=
𝐴 + 𝐵
𝑝 + 𝑞
=
𝑀
𝑝 + 𝑞
= 𝑲
O valor de K é que proporciona a solução pois: A = K.p e B = K.q
Exemplos
1) Para decompor o número 200 em duas partes A e B diretamente proporcionais a 2 e 3, montaremos
o sistema de modo que A + B = 200, cuja solução segue de:
𝐴
2
=
𝐵
3
=
𝐴 + 𝐵
5
=
200
5
= 𝟒𝟎
Fazendo A = K.p e B = K.q; temos que A = 40.2 = 80 e B=40.3 = 120
2) Determinar números A e B diretamente proporcionais a 8 e 3, sabendo-se que a diferença entre eles
é 40. Para resolver este problema basta tomar A – B = 40 e escrever:
𝐴
8
=
𝐵
3
=
𝐴 − 𝐵
5
=
40
5
= 𝟖
Fazendo A = K.p e B = K.q; temos que A = 8.8 = 64 e B = 8.3 = 24
Divisão em várias partes diretamente proporcionais
Para decompor um número M em partes x1, x2, ..., xn diretamente proporcionais a p1, p2, ..., pn, deve-
se montar um sistema com n equações e n incógnitas, sendo as somas x1 + x2 + ... + xn= M e p1 + p2 + ...
+ pn = P.
𝑥1
𝑝1
=
𝑥2
𝑝2
= ⋯ =
𝑥𝑛
𝑝𝑛
A solução segue das propriedades das proporções:
𝒙𝟏
𝒑𝟏
=
𝒙𝟐
𝒑𝟐
= ⋯ =
𝒙𝒏
𝒑𝒏
=
𝒙𝟏 + 𝒙𝟐 + ⋯ + 𝒙𝒏
𝒑𝟏 + 𝒑𝟐 + ⋯ 𝒑𝒏
=
𝑴
𝑷
= 𝑲
Observa-se que partimos do mesmo princípio da divisão em duas partes proporcionais.
Exemplos
1) Para decompor o número 240 em três partes A, B e C diretamente proporcionais a 2, 4 e 6, deve-
se montar um sistema com 3 equações e 3 incógnitas tal que A + B + C = 240 e 2 + 4 + 6 = P. Assim:
𝐴
2
=
𝐵
4
=
𝐶
6
=
𝐴 + 𝐵 + 𝐶
𝑃
=
240
12
= 𝟐𝟎
Logo: A = 20.2 = 40; B = 20.4 = 80 e C = 20.6 =120
2) Determinar números A, B e C diretamente proporcionais a 2, 4 e 6, de modo que 2A + 3B - 4C =
480
𝐴
2
=
𝐵
4
=
𝐶
6
=
2𝐴 + 3𝐵 − 4𝐶
2.2 + 3.4 − 4.6
=
480
−8
= −𝟔𝟎
Logo: A = - 60.2 = -120 ; B = - 60.4 = - 240 e C = - 60.6 = - 360.
Também existem proporções com números negativos.

50
Divisão Inversamente Proporcional
Divisão em duas partes inversamente proporcionais
Para decompor um número M em duas partes A e B inversamente proporcionais a p e q, deve-se
decompor este número M em duas partes A e B diretamente proporcionais a 1/p e 1/q, que são,
respectivamente, os inversos de p e q.
Assim basta montar o sistema com duas equações e duas incógnitas tal que A + B = M. Desse modo:
𝐴
1/𝑝
=
𝐵
1/𝑞
=
𝐴 + 𝐵
1/𝑝 + 1/𝑞
=
𝑀
1/𝑝 + 1/𝑞
=
𝑀. 𝑝. 𝑞
𝑝 + 𝑞
= 𝑲
O valor de K proporciona a solução pois: A = K/p e B = K/q.
Exemplos
1) Para decompor o número 120 em duas partes A e B inversamente proporcionais a 2 e 3, deve-se
montar o sistema tal que A + B = 120, de modo que:
𝐴
1/2
=
𝐵
1/3
=
𝐴 + 𝐵
1/2 + 1/3
=
120
5/6
=
120.6
5
= 144
Assim A = K/p → A = 144/2 = 72 e B = K/q → B = 144/3 = 48
2) Determinar números A e B inversamente proporcionais a 6 e 8, sabendo-se que a diferença entre
eles é 10. Para resolver este problema, tomamos A – B = 10. Assim:
𝐴
1/6
=
𝐵
1/8
=
𝐴 − 𝐵
1/6 − 1/8
=
10
1/24
= 240
Assim A = K/p → A = 240/6 = 40 e B = K/q → B = 240/8 = 30
Divisão em várias partes inversamente proporcionais
Para decompor um número M em n partes x1, x2, ..., xn inversamente proporcionais a p1, p2, ..., pn,
basta decompor este número M em n partes x1, x2, ..., xn diretamente proporcionais a 1/p1, 1/p2, ..., 1/pn.
A montagem do sistema com n equações e n incógnitas, assume que x1 + x2 + ... + xn= M e além disso:
𝑥1
1/𝑝1
=
𝑥2
1/𝑝2
= ⋯ =
𝑥𝑛
1/𝑝𝑛
Cuja solução segue das propriedades das proporções:
𝒙𝟏
𝟏/𝒑𝟏
=
𝒙𝟐
𝟏/𝒑𝟐
= ⋯ =
𝒙𝒏
𝟏
𝒑𝒏
=
𝒙𝟏 + 𝒙𝟐 + ⋯ + 𝒙𝒏
𝟏
𝒑𝟏
+
𝟏
𝒑𝟐
+ ⋯
𝟏
𝒑𝒏
=
𝑴
𝟏
𝒑𝟏
+
𝟏
𝒑𝟐
+ ⋯ +
𝟏
𝒑𝒏
= 𝑲
Exemplos
1) Para decompor o número 220 em três partes A, B e C inversamente proporcionais a 2, 4 e 6, deve-
se montar um sistema com 3 equações e 3 incógnitas, de modo que A + B + C = 220. Desse modo:
𝐴
1/2
=
𝐵
1/4
=
𝐶
1/6
=
𝐴 + 𝐵 + 𝐶
1/2 + 1/4 + 1/6
=
220
11/12
= 240
A solução é A = K/p1 → A = 240/2 = 120, B = K/p2 → B = 240/4 = 60 e C = K/p3 → C = 240/6 = 40
2) Para obter números A, B e C inversamente proporcionais a 2, 4 e 6, de modo que 2A + 3B - 4C =
10, devemos montar as proporções:
𝐴
1/2
=
𝐵
1/4
=
𝐶
1/6
=
2𝐴 + 3𝐵 − 4𝐶
2/2 + 3/4 − 4/6
=
10
13/12
=
120
13

51
Portanto, A = 60/13, B = 30/13 e C = 20/13
Existem proporções com números fracionários!
Divisão em partes direta e inversamente proporcionais
Divisão em duas partes direta e inversamente proporcionais
Para decompor um número M em duas partes A e B diretamente proporcionais a, c e d e inversamente
proporcionais a p e q, deve-se decompor este número M em duas partes A e B diretamente proporcionais
a c/q e d/q, basta montar um sistema com duas equações e duas incógnitas de forma que A + B = M e
além disso:
𝑨
𝒄/𝒑
=
𝑩
𝒅/𝒒
=
𝑨 + 𝑩
𝒄/𝒑 + 𝒅/𝒒
=
𝑴
𝒄/𝒑 + 𝒅/𝒒
=
𝑴. 𝒑. 𝒒
𝒄. 𝒒 + 𝒑. 𝒅
= 𝑲
O valor de K proporciona a solução pois: A = K.c/p e B = K.d/q.
Exemplos
1) Para decompor o número 58 em duas partes A e B diretamente proporcionais a 2 e 3, e,
inversamente proporcionais a 5 e 7, deve-se montar as proporções:
𝐴
2/5
=
𝐵
3/7
=
𝐴 + 𝐵
2/5 + 3/7
=
58
29/35
= 70
Assim A = K.c/p = (2/5).70 = 28 e B = K.d/q = (3/7).70 = 30
2) Para obter números A e B diretamente proporcionais a 4 e 3 e inversamente proporcionais a 6 e 8,
sabendo-se que a diferença entre eles é 21. Para resolver este problema basta escrever que A – B = 21
devemos resolver as proporções:
𝐴
4/6
=
𝐵
3/8
=
𝐴 − 𝐵
4/6 − 3/8
=
21
7/24
= 72
Assim A = K.c/p = (4/6).72 = 48 e B = K.d/q = (3/8).72 = 27
Divisão em n partes direta e inversamente proporcionais
Para decompor um número M em n partes x1, x2, ..., xn diretamente proporcionais a p1, p2, ..., pn e
inversamente proporcionais a q1, q2, ..., qn, basta decompor este número M em n partes x1, x2, ..., xn
diretamente proporcionais a p1/q1, p2/q2, ..., pn/qn.
A montagem do sistema com n equações e n incógnitas exige que x1 + x2 + ... + xn = M e além disso
𝑥1
𝑝1/𝑞1
=
𝑥2
𝑝2/𝑞2
= ⋯ =
𝑥𝑛
𝑝𝑛/𝑞𝑛
𝒙𝟏
𝒑𝟏/𝒒𝟏
=
𝒙𝟐
𝒑𝟐/𝒒𝟐
= ⋯ =
𝒙𝒏
𝒑𝒏
𝒒𝒏
=
𝒙𝒏 + 𝒙𝟐 + ⋯ + 𝒙𝒏
𝒑𝟏
𝒒𝟏
+
𝒑𝟐
𝒒𝟐
+ ⋯ +
𝒑𝒏
𝒒𝒏
= 𝑲
Exemplos
1) Para decompor o número 115 em três partes A, B e C diretamente proporcionais a 1, 2 e 3 e
inversamente proporcionais a 4, 5 e 6, deve-se montar um sistema com 3 equações e 3 incógnitas de
forma que A + B + C = 115 e também:
𝐴
1/4
=
𝐵
2/5
=
𝐶
3/6
=
𝐴 + 𝐵 + 𝐶
1/4 + 2/5 + 3/6
=
115
23/20
= 100

52
Logo A = K.p1/q1 = (1/4)100 = 25, B = K.p2/q2 = (2/5)100 = 40 e C = K.p3/q3 = (3/6)100 = 50
2) Determinar números A, B e C diretamente proporcionais a 1, 10 e 2 e inversamente proporcionais a
2, 4 e 5, de modo que 2A + 3B - 4C = 10.
A montagem do problema fica na forma:
𝐴
1/2
=
𝐵
10/4
=
𝐶
2/5
=
2𝐴 + 3𝐵 − 4𝐶
2/2 + 30/4 − 8/5
=
10
69/10
=
100
69
A solução é A = K.p1/q1 = 50/69, B = K.p2/q2 = 250/69 e C = K.p3/q3 = 40/69
Problemas envolvendo Divisão Proporcional
1) As famílias de duas irmãs, Alda e Berta, vivem na mesma casa e a divisão de despesas mensais é
proporcional ao número de pessoas de cada família. Na família de Alda são três pessoas e na de Berta,
cinco. Se a despesa, num certo mês foi de R$ 1.280,00, quanto pagou, em reais, a família de Alda?
A) 320,00
B) 410,00
C) 450,00
D) 480,00
E) 520,00
Alda: A = 3 pessoas
Berta: B = 5 pessoas
A + B = 1280
𝐴
3
+
𝐵
5
=
𝐴 + 𝐵
3 + 5
=
1280
8
= 160
A = K.p = 160.3 = 480
Resposta: D
2) Dois ajudantes foram incumbidos de auxiliar no transporte de 21 caixas que continham
equipamentos elétricos. Para executar essa tarefa, eles dividiram o total de caixas entre si, na razão
inversa de suas respectivas idades. Se ao mais jovem, que tinha 24 anos, coube transportar 12 caixas,
então, a idade do ajudante mais velho, em anos era?
A) 32
B) 34
C) 35
D) 36
E) 38
v = idade do mais velho
Temos que a quantidade de caixas carregadas pelo mais novo:
Qn = 12
Pela regra geral da divisão temos:
Qn = k.1/24 → 12 = k/24 → k = 288
A quantidade de caixas carregadas pelo mais velho é: 21 – 12 = 9
Pela regra geral da divisão temos:
Qv = k.1/v → 9 = 288/v → v = 32 anos
Resposta: A
3) Em uma seção há duas funcionárias, uma com 20 anos de idade e a outra com 30. Um total de 150
processos foi dividido entre elas, em quantidades inversamente proporcionais às suas respectivas idades.
Qual o número de processos recebido pela mais jovem?
A) 90
B) 80
C) 60
D) 50
E) 30

53
Estamos trabalhando aqui com divisão em duas partes inversamente proporcionais e para a resolução
da mesma temos que:
𝑨
𝟏/𝒑
=
𝑩
𝟏/𝒒
=
𝑨 + 𝑩
𝟏/𝒑 + 𝟏/𝒒
=
𝑴
𝟏/𝒑 + 𝟏/𝒒
=
𝑴. 𝒑. 𝒒
𝒑 + 𝒒
= 𝑲
O valor de K proporciona a solução pois: A = K/p e B = K/q.
Vamos chamar as funcionárias de p e q respectivamente:
p = 20 anos (funcionária de menor idade)
q = 30 anos
Como será dividido os processos entre as duas, logo cada uma ficará com A e B partes que totalizam
150:
A + B = 150 processos
𝐴
1/𝑝
=
𝐵
1/𝑞
=
150
1/20 + 1/30
=
150
1/20 + 1/30
=
150.20.30
20 + 30
=
90000
50
= 𝟏𝟖𝟎𝟎
A = k/p → A = 1800 / 20 → A = 90 processos.
Questões
01. (Pref. Paulistana/PI – Professor de Matemática – IMA) Uma herança de R$ 750.000,00 deve ser
repartida entre três herdeiros, em partes proporcionais a suas idades que são de 5, 8 e 12 anos. O mais
velho receberá o valor de:
(A) R$ 420.000,00
(B) R$ 250.000,00
(C) R$ 360.000,00
(D) R$ 400.000,00
(E) R$ 350.000,00
02. (TRF/3ªRegião– Técnico Judiciário – FCC) Quatro funcionários dividirão, em partes diretamente
proporcionais aos anos dedicados para a empresa, um bônus de R$36.000,00. Sabe-se que dentre esses
quatro funcionários um deles já possui 2 anos trabalhados, outro possui 7 anos trabalhados, outro possui
6 anos trabalhados e o outro terá direito, nessa divisão, à quantia de R$6.000,00. Dessa maneira, o
número de anos dedicados para a empresa, desse último funcionário citado, é igual a
(A) 5.
(B) 7.
(C) 2.
(D) 3.
(E) 4.
03. (Câmara de São Paulo/SP – Técnico Administrativo – FCC) Uma prefeitura destinou a quantia
de 54 milhões de reais para a construção de três escolas de educação infantil. A área a ser construída
em cada escola é, respectivamente, 1.500 m², 1.200 m² e 900 m² e a quantia destinada à cada escola é
diretamente proporcional a área a ser construída.
Sendo assim, a quantia destinada à construção da escola com 1.500 m² é, em reais, igual a
(A) 22,5 milhões.
(B) 13,5 milhões.
(C) 15 milhões.
(D) 27 milhões.
(E) 21,75 milhões.
04. (SABESP – Atendente a Clientes 01 – FCC) Uma empresa quer doar a três funcionários um
bônus de R$ 45.750,00. Será feita uma divisão proporcional ao tempo de serviço de cada um deles. Sr.
Fortes trabalhou durante 12 anos e 8 meses. Sra. Lourdes trabalhou durante 9 anos e 7 meses e Srta.
Matilde trabalhou durante 3 anos e 2 meses. O valor, em reais, que a Srta. Matilde recebeu a menos que
o Sr. Fortes é

54
(A) 17.100,00.
(B) 5.700,00.
(C) 22.800,00.
(D) 17.250,00.
(E) 15.000,00.
05. (SESP/MT – Perito Oficial Criminal – FUNCAB) Maria, Júlia e Carla dividirão R$ 72.000,00 em
partes inversamente proporcionais às suas idades. Sabendo que Maria tem 8 anos, Júlia, 12 e Carla, 24,
determine quanto receberá quem ficar com a maior parte da divisão.
(A) R$ 36.000,00
(B) R$ 60.000,00
(C) R$ 48.000,00
(D) R$ 24.000,00
(E) R$ 30.000,00
06. (PC/SP – Fotógrafo Perito – VUNESP) Uma verba de R$ 65.000,00 será alocada a três projetos
diferentes. A divisão desse dinheiro será realizada de forma diretamente proporcional aos graus de
importância dos projetos, que são, respectivamente, 2, 4 e 7. Dessa maneira, a quantia que o projeto
mais importante receberá ultrapassa a metade do total da verba em
(A) R$ 2.500,00.
(B) R$ 9.000,00.
(C) R$ 1.000,00.
(D) R$ 5.000,00.
(E) R$ 7.500,00.
07. (PC/SP – Atendente de Necrotério Policial – VUNESP) No ano de 2008, a Secretaria Nacional
de Segurança Pública divulgou o Relatório Descritivo com o Perfil dos Institutos de Medicina Legal (IML)
brasileiros. Nesse relatório, consta que, em 2006, as quantidades de IMLs nos Estados do Espírito Santo,
de Minas Gerais, do Rio de Janeiro e de São Paulo eram, respectivamente, 2, 20, 9 e 64. Supondo-se
que uma verba federal de R$ 190 milhões fosse destinada aos IMLs desses Estados, e a divisão dessa
verba fosse feita de forma diretamente proporcional a essas quantidades de IMLs por estado, o Estado
de São Paulo receberia o valor, em milhões, de
(A) R$ 128.
(B) R$ 165,5.
(C) R$ 98.
(D) R$ 156.
(E) R$ 47,5.
08. (UFABC/SP – Tradutor e Intérprete de Linguagens de Sinais – VUNESP) Alice, Bianca e Carla
trabalharam na organização da biblioteca da escola e, juntas, receberam como pagamento um total de
R$900,00. Como cada uma delas trabalhou um número diferente de horas, as três decidiram que a divisão
do dinheiro deveria ser proporcional ao tempo trabalhado. Alice trabalhou por 4 horas, e Bianca, que
trabalhou 30 minutos menos do que Alice, recebeu R$210,00. A parte devida a Carla foi de
(A) R$400,00.
(B) R$425,00.
(C) R$450,00.
(D) R$475,00.
(E) R$500,00.
09. (EMTU/SP – Agente de Fiscalização – CAIPIMES) Uma calçada retilínea com 171 metros precisa
ser dividida em três pedaços de comprimentos proporcionais aos números 2, 3 e 4. O maior pedaço
deverá medir:
(A) 78 metros.
(B) 82 metros.
(C) 76 metros.
(D) 80 metros.

55
10. (METRÔ/SP - Agente de Segurança Metroviária I - FCC) Repartir dinheiro proporcionalmente às
vezes dá até briga. Os mais altos querem que seja divisão proporcional à altura. Os mais velhos querem
que seja divisão proporcional à idade. Nesse caso, Roberto com 1,75 m e 25 anos e Mônica, sua irmã,
com 1,50 m e 20 anos precisavam dividir proporcionalmente a quantia de R$ 29.250,00. Decidiram, no
par ou ímpar, quem escolheria um dos critérios: altura ou idade. Mônica ganhou e decidiu a maneira que
mais lhe favorecia. O valor, em reais, que Mônica recebeu a mais do que pela divisão no outro critério, é
igual a
(A) 500.
(B) 400.
(C) 300.
(D) 250.
(E) 50.
Comentários
01. Resposta: C
5x + 8x + 12x = 750.000
25x = 750.000
x = 30.000
O mais velho receberá: 1230000=360000
02. Resposta: D
2x + 7x + 6x + 6000 = 36000
15x = 30000
x = 2000
Como o último recebeu R$ 6.000,00, significa que ele se dedicou 3 anos a empresa, pois 2000.3 =
6000
03. Resposta: A
1500x + 1200x + 900x = 54000000
3600x = 54000000
x = 15000
Escola de 1500 m²: 1500.15000 = 22500000 = 22,5 milhões.
04. Resposta: A
* Fortes: 12 anos e 8 meses = 12.12 + 8 = 144 + 8 = 152 meses
* Lourdes: 9 anos e 7 meses = 9.12 + 7 = 108 + 7 = 115 meses
* Matilde: 3 anos e 2 meses = 3.12 + 2 = 36 + 2 = 38 meses
* TOTAL: 152 + 115 + 38 = 305 meses
* Vamos chamar a quantidade que cada um vai receber de F, L e M.
𝑭
𝟏𝟓𝟐
=
𝑳
𝟏𝟏𝟓
=
𝑴
𝟑𝟖
=
𝑭 + 𝑳 + 𝑴
𝟏𝟓𝟐 + 𝟏𝟏𝟓 + 𝟑𝟖
=
𝟒𝟓𝟕𝟓𝟎
𝟑𝟎𝟓
= 𝟏𝟓𝟎
Agora, vamos calcular o valor que M e F receberam:
𝑴
𝟑𝟖
= 𝟏𝟓𝟎
M = 38 . 150 = R$ 5 700,00
𝑭
𝟏𝟓𝟐
= 𝟏𝟓𝟎
F = 152 . 150 = R$ 22 800,00
Por fim, a diferença é: 22 800 – 5700 = R$ 17 100,00
05. Resposta: A
M + J + C = 72000

56
𝑀
1
1
8
=
𝐽
1
1
12
=
𝐶
1
1
24
=
𝑀 +𝐽+𝐶
1
3+2+1
24
=
72000
1
6
24
=
72000 .24
6 .1
= 72000 . 4 = 288000
A maior parte ficará para a mais nova (grandeza inversamente proporcional).
Assim:
8.𝑀
1
= 288000
8.M = 288 000 → M = 288 000 / 8 → M = R$ 36 000,00
06. Resposta: A
Temos que A + B + C = 65 000, por grau de importância temos:
A = K.2
B = K.4
C = K.7
Aplicando na propriedade da divisão proporcional:
𝐴
2
+
𝐵
4
+
𝐶
7
=
𝐴 + 𝐵 + 𝐶
2 + 4 + 7
=
65 000
13
= 5000
Temos que K = 5000, aplicando acima, vamos descobrir o valor atribuído a cada um projeto:
A = 5000 .2 = 10 000
B = 5000.4 = 20 000
C = 5000.7 = 35 000
Como ele quer saber quanto o projeto de maior importância superou a metade da verba total, temos:
Metade da verba total = 65 000/2 = 32 500
Como o valor do projeto de maior importância é 35 000, logo 35 000 – 32 500 = 2 500
07. Resposta: A
Temos que E + M + R + S = 190 milhões
Então:
𝐸
2
+
𝑀
20
+
𝑅
9
+
𝑆
64
=
𝐸 + 𝑀 + 𝑅 + 𝑆
2 + 20 + 9 + 64
=
190 000 0000
95
= 2 000 000
Como queremos saber de o valor de São Paulo:
S = 2 000 000 . 64 = 128 000 000 ou 128 milhões.
08. Resposta: C
Alice: 4horas = 240 minutos
Bianca: 3 horas 30 minutos = 210 minutos
K: constante
210.k = 210
k = 1, cada minuto vale R$ 1,00
Carla: Y
240 + 210 + Y = 900
Y = 900 - 450
Y = 450
09. Resposta: C
𝑥
2
+
𝑦
3
+
𝑧
4
=
171
9
= 19
y = 19.4 = 76 ou
2x + 3x + 4x = 171
9x = 171 → x = 19
Maior pedaço: 4x = 4.19 = 76 metros
10. Resposta: A
Pela altura:
R + M = 29250

57
𝑅
1,75
+
𝑀
1,50
=
29250
1,75 + 1,5
=
29250
3,25
= 9000
Mônica: 1, 5.9000=13500
Pela idade
𝑅
25
+
𝑀
20
=
29250
45
= 650
Mônica: 20.650 = 13000
13500 – 13000 = 500
REGRA DE TRÊS SIMPLES
Os problemas que envolvem duas grandezas diretamente ou inversamente proporcionais podem ser
resolvidos através de um processo prático, chamado regra de três simples7
.
Vejamos a tabela abaixo:
Exemplos
01. Um carro faz 180 km com 15L de álcool. Quantos litros de álcool esse carro gastaria para percorrer
210 km?
O problema envolve duas grandezas: distância e litros de álcool.
Indiquemos por x o número de litros de álcool a ser consumido.
Coloquemos as grandezas de mesma espécie em uma mesma coluna e as grandezas de espécies
diferentes que se correspondem em uma mesma linha:
Na coluna em que aparece a variável x (“litros de álcool”), vamos colocar uma flecha:
7
MARIANO, Fabrício. Matemática Financeira para Concursos. 3ª Edição. Rio de Janeiro. Elsevier,2013.

58
Observe que, se duplicarmos a distância, o consumo de álcool também duplica. Então, as grandezas
distância e litros de álcool são diretamente proporcionais. No esquema que estamos montando,
indicamos esse fato colocando uma flecha na coluna “distância” no mesmo sentido da flecha da coluna
“litros de álcool”:
Armando a proporção pela orientação das flechas, temos:
180
210
=
15
𝑥
→ 𝑐𝑜𝑚𝑜 180 𝑒 210 𝑝𝑜𝑑𝑒𝑚 𝑠𝑒𝑟 𝑠𝑖𝑚𝑝𝑙𝑖𝑓𝑖𝑐𝑎𝑑𝑜𝑠 𝑝𝑜𝑟 30, 𝑡𝑒𝑚𝑜𝑠:
180: 30
210: 30
=
15
𝑥
1806
2107
=
15
𝑥
→ 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑛𝑑𝑜 𝑐𝑟𝑢𝑧𝑎𝑑𝑜(𝑝𝑟𝑜𝑑𝑢𝑡𝑜 𝑑𝑜 𝑚𝑒𝑖𝑜 𝑝𝑒𝑙𝑜𝑠 𝑒𝑥𝑡𝑟𝑒𝑚𝑜𝑠) → 6𝑥 = 7.15
6𝑥 = 105 → 𝑥 =
105
6
= 𝟏𝟕, 𝟓
Resposta: O carro gastaria 17,5 L de álcool.
02. Viajando de automóvel, à velocidade de 50 km/h, eu gastaria 7 h para fazer certo percurso.
Aumentando a velocidade para 80 km/h, em quanto tempo farei esse percurso?
Indicando por x o número de horas e colocando as grandezas de mesma espécie em uma mesma
coluna e as grandezas de espécies diferentes que se correspondem em uma mesma linha, temos:
Na coluna em que aparece a variável x (“tempo”), vamos colocar uma flecha:
Observe que, se duplicarmos a velocidade, o tempo fica reduzido à metade. Isso significa que as
grandezas velocidade e tempo são inversamente proporcionais. No nosso esquema, esse fato é
indicado colocando-se na coluna “velocidade” uma flecha em sentido contrário ao da flecha da coluna
“tempo”:
Na montagem da proporção devemos seguir o sentido das flechas. Assim, temos:
7
𝑥
=
80
50
, 𝑖𝑛𝑣𝑒𝑟𝑡𝑒𝑚𝑜𝑠 𝑒𝑠𝑡𝑒 𝑙𝑎𝑑𝑜 →
7
𝑥
=
808
505
→ 7.5 = 8. 𝑥 → 𝑥 =
35
8
→ 𝑥 = 4,375 ℎ𝑜𝑟𝑎𝑠

59
Como 0,375hora corresponde a 22 minutos aproximadamente (0,375 x 60 minutos), então o percurso
será feito em 4 horas e 22 minutos aproximadamente.
03. Ao participar de um treino de fórmula Indy, um competidor, imprimindo a velocidade média de 180
km/h, faz o percurso em 20 segundos. Se a sua velocidade fosse de 300 km/h, que tempo teria gasto no
percurso?
Vamos representar pela letra x o tempo procurado.
Estamos relacionando dois valores da grandeza velocidade (180 km/h e 300 km/h) com dois valores
da grandeza tempo (20 s e x s).
Queremos determinar um desses valores, conhecidos os outros três.
Se duplicarmos a velocidade inicial do carro, o tempo gasto para fazer o percurso cairá para a metade;
logo, as grandezas são inversamente proporcionais. Assim, os números 180 e 300 são inversamente
proporcionais aos números 20 e x.
Daí temos:
180.20 = 300. 𝑥 → 300𝑥 = 3600 → 𝑥 =
3600
300
→ 𝑥 = 12
Conclui-se, então, que se o competidor tivesse andando em 300 km/h, teria gasto 12 segundos para
realizar o percurso.
Questões
01. (PM/SP – Oficial Administrativo – VUNESP) Em 3 de maio de 2014, o jornal Folha de S. Paulo
publicou a seguinte informação sobre o número de casos de dengue na cidade de Campinas.
De acordo com essas informações, o número de casos registrados na cidade de Campinas, até 28 de
abril de 2014, teve um aumento em relação ao número de casos registrados em 2007, aproximadamente,
de
(A) 70%.
(B) 65%.
(C) 60%.
(D) 55%.
(E) 50%.
02. (FUNDUNESP – Assistente Administrativo – VUNESP) Um título foi pago com 10% de desconto
sobre o valor total. Sabendo-se que o valor pago foi de R$ 315,00, é correto afirmar que o valor total
desse título era de
(A) R$ 345,00.
(B) R$ 346,50.
(C) R$ 350,00.
(D) R$ 358,50.
(E) R$ 360,00.

60
03. (Pref. Imaruí – Agente Educador – Pref. Imaruí) Manoel vendeu seu carro por R$27.000,00(vinte
e sete mil reais) e teve um prejuízo de 10%(dez por cento) sobre o valor de custo do tal veículo, por
quanto Manoel adquiriu o carro em questão?
(A) R$24.300,00
(B) R$29.700,00
(C) R$30.000,00
(D)R$33.000,00
(E) R$36.000,00
04. (Pref. Guarujá/SP – Professor de Matemática – CAIPIMES) Em um mapa, cuja escala era
1:15.104
, a menor distância entre dois pontos A e B, medida com a régua, era de 12 centímetros. Isso
significa que essa distância, em termos reais, é de aproximadamente:
(A) 180 quilômetros.
(B) 1.800 metros.
(C) 18 quilômetros.
(D) 180 metros.
05. (CEFET – Auxiliar em Administração – CESGRANRIO) A Bahia (...) é o maior produtor de cobre
do Brasil. Por ano, saem do estado 280 mil toneladas, das quais 80 mil são exportadas.
O Globo, Rio de Janeiro: ed. Globo, 12 mar. 2014, p. 24.
Da quantidade total de cobre que sai anualmente do Estado da Bahia, são exportados,
aproximadamente,
(A) 29%
(B) 36%
(C) 40%
(D) 56%
(E) 80%
06. (PM/SP – Oficial Administrativo – VUNESP) Um comerciante comprou uma caixa com 90 balas
e irá vender cada uma delas por R$ 0,45. Sabendo que esse comerciante retirou 9 balas dessa caixa
para consumo próprio, então, para receber o mesmo valor que teria com a venda das 90 balas, ele terá
que vender cada bala restante na caixa por:
(A) R$ 0,50.
(B) R$ 0,55.
(C) R$ 0,60.
(D) R$ 0,65.
(E) R$ 0,70.
07. (PM/SP – Oficial Administrativo – VUNESP) Em 25 de maio de 2014, o jornal Folha de S. Paulo
publicou a seguinte informação sobre a capacidade de retirada de água dos sistemas de abastecimento,
em metros cúbicos por segundo (m3
/s):
De acordo com essas informações, o número de segundos necessários para que o sistema Rio Grande
retire a mesma quantidade de água que o sistema Cantareira retira em um segundo é:

61
(A) 5,4.
(B) 5,8.
(C) 6,3.
(D) 6,6.
(E) 6,9.
08. (FUNDUNESP – Auxiliar Administrativo – VUNESP) Certo material para laboratório foi adquirido
com desconto de 10% sobre o preço normal de venda. Sabendo-se que o valor pago nesse material foi
R$ 1.170,00, é possível afirmar corretamente que seu preço normal de venda é
(A) R$ 1.285,00.
(B) R$ 1.300,00.
(C) R$ 1.315,00.
(D) R$ 1.387,00.
(E) R$ 1.400,00.
09. (PC/SP – Oficial Administrativo – VUNESP) A mais antiga das funções do Instituto Médico Legal
(IML) é a necropsia. Num determinado período, do total de atendimentos do IML, 30% foram necropsias.
Do restante dos atendimentos, todos feitos a indivíduos vivos, 14% procediam de acidentes no trânsito,
correspondendo a 588. Pode-se concluir que o total de necropsias feitas pelo IML, nesse período, foi
(A) 2500.
(B) 1600.
(C) 2200.
(D) 3200.
(E) 1800.
10. (SAAE/SP – Auxiliar de Manutenção Geral – VUNESP) A expectativa de vida do Sr. Joel é de 75
anos e, neste ano, ele completa 60 anos. Segundo esta expectativa, pode-se afirmar que a fração de vida
que ele já viveu é
(A)
4
7
(B)
5
6
(C)
4
5
(D)
3
4
(E)
2
3
11. (SAAE/SP – Auxiliar de Manutenção Geral – VUNESP) Foram digitados 10 livros de 200 páginas
cada um e armazenados em 0,0001 da capacidade de um microcomputador. Utilizando-se a capacidade
total desse microcomputador, o número de livros com 200 páginas que é possível armazenar é
(A) 100.
(B) 1000.
(C) 10000.
(D) 100000.
(E) 1000000.
12. (IF/GO – Assistente de Alunos – UFG) Leia o fragmento a seguir
A produção brasileira de arroz projetada para 2023 é de 13,32 milhões de toneladas, correspondendo
a um aumento de 11% em relação à produção de 2013.
Disponível em: <http://www.agricultura.gov.br/arq_editor/projecoes-ver saoatualizada.pdf>. Acesso em: 24 fev. 2014. (Adaptado).
De acordo com as informações, em 2023, a produção de arroz excederá a produção de 2013, em
milhões de toneladas, em:
(A) 1,46
(B) 1,37
(C) 1,32
(D) 1,22

62
13. (PRODAM/AM – Auxiliar de Motorista – FUNCAB) Numa transportadora, 15 caminhões de
mesma capacidade transportam toda a carga de um galpão em quatro horas. Se três deles quebrassem,
em quanto tempo os outros caminhões fariam o mesmo trabalho?
(A) 3 h 12 min
(B) 5 h
(C) 5 h 30 min
(D) 6 h
(E) 6 h 15 min
14. (Câm. de São Paulo/SP – Técnico Administrativo – FCC) Uma receita para fazer 35 bolachas
utiliza 225 gramas de açúcar. Mantendo-se as mesmas proporções da receita, a quantidade de açúcar
necessária para fazer 224 bolachas é
(A) 14,4 quilogramas.
(B) 1,8 quilogramas.
(C) 1,44 quilogramas.
(D) 1,88 quilogramas.
(E) 0,9 quilogramas.
15. (METRÔ/SP – Usinador Ferramenteiro – FCC) Laerte comprou 18 litros de tinta látex que, de
acordo com as instruções na lata, rende 200m² com uma demão de tinta. Se Laerte seguir corretamente
as instruções da lata, e sem desperdício, depois de pintar 60 m² de parede com duas demãos de tinta
látex, sobrarão na lata de tinta comprada por ele
(A) 6,8L.
(B) 6,6L.
(C) 10,8L.
(D) 7,8L.
(E) 7,2L.
Comentários
01. Resposta: E
Utilizaremos uma regra de três simples diretamente proporcional:
ano %
11442 ------- 100
17136 ------- x
11442.x = 17136. 100 x = 1713600 / 11442 = 149,8% (aproximado)
149,8% – 100% = 49,8%
Aproximando o valor, teremos 50%
02. Resposta: C
Se R$ 315,00 já está com o desconto de 10%, então R$ 315,00 equivale a 90% (100% - 10%).
Utilizaremos uma regra de três simples diretamente proporcional:
$ %
315 ------- 90
x ------- 100
90.x = 315. 100 x = 31500 / 90 = R$ 350,00
03. Resposta: C
Como ele teve um prejuízo de 10%, quer dizer 27000 é 90% do valor total, regra de três simples
diretamente proporcional.
Valor %
27000 ------ 90
X ------- 100
27000
𝑥
=
909
10010 →
27000
𝑥
=
9
10
→ 9.x = 27000.10 → 9x = 270000 → x = 30000.

63
04. Resposta: C
1: 15.104
equivale a 1:150000, ou seja, para cada 1 cm do mapa, teremos 150.000 cm no tamanho
real. Assim, faremos uma regra de três simples diretamente proporcional:
mapa real
1 --------- 150000
12 --------- x
1.x = 12. 150000 x = 1.800.000 cm = 18 km
05. Resposta: A
Faremos uma regra de três simples:
cobre %
280 --------- 100
80 ---------- x
280.x = 80. 100 x = 8000 / 280 x = 28,57%
06. Resposta: A
Vamos utilizar uma regra de três simples:
Balas $
1 ----------- 0,45
90 ---------- x
1.x = 0,45. 90
x = R$ 40,50 (total)
* 90 – 9 = 81 balas
Novamente, vamos utilizar uma regra de três simples:
Balas $
81 ----------- 40,50
1 ------------ y
81.y = 1 . 40,50
y = 40,50 / 81
y = R$ 0,50 (cada bala)
07. Resposta: D
Utilizaremos uma regra de três simples INVERSA:
m3
seg
33 ------- 1
5 ------- x
5.x = 33 . 1 x = 33 / 5 = 6,6 seg
08. Resposta: B
$ %
1170 ------- 90
x ------- 100
90.x = 1170 . 100 x = 117000 / 90 = R$ 1.300,00
09. Resposta: E
O restante de atendimento é de 100% – 30% = 70% (restante)
Restante:
atendimentos %
588 ------------ 14
x ------------ 100
14.x = 588 . 100 x = 58800 / 14 = 4200 atendimentos (restante)
Total:
atendimentos %
4200 ------------ 70
x ------------ 30
70.x = 4200 . 30 x = 126000 / 70 = 1800 atendimentos

64
10. Resposta: C
Considerando 75 anos o inteiro (1), utilizaremos uma regra de três simples:
idade fração
75 ------------ 1
60 ------------ x
75.x = 60 . 1 x = 60 / 75 = 4 / 5 (simplificando por 15)
11. Resposta: D
Neste caso, a capacidade total é representada por 1 (inteiro).
Assim, utilizaremos uma regra de três simples:
livros capacidade
10 ------------ 0,0001
x ------------ 1
0,0001.x = 10 . 1 x = 10 / 0,0001 = 100.000 livros
12. Resposta: C
Toneladas %
13,32 ----------- 111
x ------------- 11
111 . x = 13,32 . 11
x = 146,52 / 111
x = 1,32
13. Resposta: B
Vamos utilizar uma Regra de Três Simples Inversa, pois, quanto menos caminhões tivermos, mais
horas demorará para transportar a carga:
caminhões horas
15 ---------------- 4
(15 – 3) ------------- x
12.x = 4 . 15 → x = 60 / 12 → x = 5 h
14. Resposta: C
Bolachas açúcar
35----------------225
224----------------x
𝑥 =
224.225
35
= 1440 𝑔𝑟𝑎𝑚𝑎𝑠 = 1,44 𝑞𝑢𝑖𝑙𝑜𝑔𝑟𝑎𝑚𝑎𝑠
15. Resposta: E
18L----200m²
x-------120
x=10,8L
Ou seja, pra 120m² (duas demãos de 60 m²) ele vai gastar 10,8 l, então sobraram:
18-10,8=7,2L
REGRA DE TRÊS COMPOSTA
O processo usado para resolver problemas que envolvem mais de duas grandezas, diretamente ou
inversamente proporcionais, é chamado regra de três composta8
.
Exemplos
01. Em 4 dias 8 máquinas produziram 160 peças. Em quanto tempo 6 máquinas iguais às primeiras
produziriam 300 dessas peças?
Indiquemos o número de dias por x. Coloquemos as grandezas de mesma espécie em uma só coluna
e as grandezas de espécies diferentes que se correspondem em uma mesma linha. Na coluna em que
aparece a variável x (“dias”), coloquemos uma flecha:
8
MARIANO, Fabrício. Matemática Financeira para Concursos. 3ª Edição. Rio de Janeiro. Elsevier,2013.

65
Iremos comparar cada grandeza com aquela em que está o x.
As grandezas peças e dias são diretamente proporcionais. No nosso esquema isso será indicado
colocando-se na coluna “peças” uma flecha no mesmo sentido da flecha da coluna “dias”:
As grandezas máquinas e dias são inversamente proporcionais (se aumentar o número de máquinas
precisaremos de menos dias). No nosso esquema isso será indicado colocando-se na coluna (máquinas)
uma flecha no sentido contrário ao da flecha da coluna “dias”:
Agora vamos montar a proporção, igualando a razão que contém o x, que é
x
4
, com o produto das
outras razões, obtidas segundo a orientação das flechas 





300
160
.
8
6
:
Simplificando as proporções obtemos:
4
𝑥
=
2
5
→ 2𝑥 = 4.5 → 𝑥 =
4.5
2
→ 𝑥 = 10
Resposta: Em 10 dias.
02. Uma empreiteira contratou 210 pessoas para pavimentar uma estrada de 300 km em 1 ano. Após
4 meses de serviço, apenas 75 km estavam pavimentados. Quantos empregados ainda devem ser
contratados para que a obra seja concluída no tempo previsto?
Iremos comparar cada grandeza com aquela em que está o x.
As grandezas “pessoas” e “tempo” são inversamente proporcionais (duplicando o número de
pessoas, o tempo fica reduzido à metade). No nosso esquema isso será indicado colocando-se na coluna
“tempo” uma flecha no sentido contrário ao da flecha da coluna “pessoas”:
As grandezas “pessoas” e “estrada” são diretamente proporcionais. No nosso esquema isso será
indicado colocando-se na coluna “estrada” uma flecha no mesmo sentido da flecha da coluna “pessoas”:

66
Como já haviam 210 pessoas trabalhando, logo 315 – 210 = 105 pessoas.
Reposta: Devem ser contratados 105 pessoas.
Questões
01. (Câm. de São Paulo/SP – Técnico Administrativo – FCC) O trabalho de varrição de 6.000 m² de
calçada é feita em um dia de trabalho por 18 varredores trabalhando 5 horas por dia. Mantendo-se as
mesmas proporções, 15 varredores varrerão 7.500 m² de calçadas, em um dia, trabalhando por dia, o
tempo de
(A) 8 horas e 15 minutos.
(B) 9 horas.
(C) 7 horas e 45 minutos.
(D) 7 horas e 30 minutos.
(E) 5 horas e 30 minutos.
02. (Pref. Corbélia/PR – Contador – FAUEL) Uma equipe constituída por 20 operários, trabalhando
8 horas por dia durante 60 dias, realiza o calçamento de uma área igual a 4800 m². Se essa equipe fosse
constituída por 15 operários, trabalhando 10 horas por dia, durante 80 dias, faria o calçamento de uma
área igual a:
(A) 4500 m²
(B) 5000 m²
(C) 5200 m²
(D) 6000 m²
(E) 6200 m²
03. (PC/SP – Oficial Administrativo – VUNESP) Dez funcionários de uma repartição trabalham 8
horas por dia, durante 27 dias, para atender certo número de pessoas. Se um funcionário doente foi
afastado por tempo indeterminado e outro se aposentou, o total de dias que os funcionários restantes
levarão para atender o mesmo número de pessoas, trabalhando uma hora a mais por dia, no mesmo
ritmo de trabalho, será:
(A) 29.
(B) 30.
(C) 33.
(D) 28.
(E) 31.
04. (TRF/3ª Região – Técnico Judiciário – FCC) Sabe-se que uma máquina copiadora imprime 80
cópias em 1 minuto e 15 segundos. O tempo necessário para que 7 máquinas copiadoras, de mesma
capacidade que a primeira citada, possam imprimir 3360 cópias é de
(A) 15 minutos.
(B) 3 minutos e 45 segundos.
(C) 7 minutos e 30 segundos.
(D) 4 minutos e 50 segundos.
(E) 7 minutos.

67
05. (METRÔ/SP – Analista Desenvolvimento Gestão Júnior – FCC) Para inaugurar no prazo a
estação XYZ do Metrô, o prefeito da cidade obteve a informação de que os 128 operários, de mesma
capacidade produtiva, contratados para os trabalhos finais, trabalhando 6 horas por dia, terminariam a
obra em 42 dias. Como a obra tem que ser terminada em 24 dias, o prefeito autorizou a contratação de
mais operários, e que todos os operários (já contratados e novas contratações) trabalhassem 8 horas por
dia. O número de operários contratados, além dos 128 que já estavam trabalhando, para que a obra seja
concluída em 24 dias, foi igual a
(A) 40.
(B) 16.
(C) 80.
(D) 20.
(E) 32.
06. (PRODAM/AM – Assistente – FUNCAB) Para digitalizar 1.000 fichas de cadastro, 16 assistentes
trabalharam durante dez dias, seis horas por dia. Dez assistentes, para digitalizar 2.000 fichas do mesmo
modelo de cadastro, trabalhando oito horas por dia, executarão a tarefa em quantos dias?
(A) 14
(B) 16
(C) 18
(D) 20
(E) 24
07. (CEFET – Auxiliar em Administração – CESGRANRIO) No Brasil, uma família de 4 pessoas
produz, em média, 13 kg de lixo em 5 dias. Mantida a mesma proporção, em quantos dias uma família de
5 pessoas produzirá 65 kg de lixo?
(A) 10
(B) 16
(C) 20
(D) 32
(E) 40
08. (UFPE – Assistente em Administração – COVEST) Na safra passada, um fazendeiro usou 15
trabalhadores para cortar sua plantação de cana de 210 hectares. Trabalhando 7 horas por dia, os
trabalhadores concluíram o trabalho em 6 dias exatos. Este ano, o fazendeiro plantou 480 hectares de
cana e dispõe de 20 trabalhadores dispostos a trabalhar 6 horas por dia. Em quantos dias o trabalho
ficará concluído?
Obs.: Admita que todos os trabalhadores tenham a mesma capacidade de trabalho.
(A) 10 dias
(B) 11 dias
(C) 12 dias
(D) 13 dias
(E) 14 dias
09. (BNB – Analista Bancário – FGV) Em uma agência bancária, dois caixas atendem em média seis
clientes em 10 minutos. Considere que, nesta agência, todos os caixas trabalham com a mesma eficiência
e que a média citada sempre é mantida. Assim, o tempo médio necessário para que cinco caixas atendam
45 clientes é de:
(A) 45 minutos;
(B) 30 minutos;
(C) 20 minutos;
(D) 15 minutos;
(E) 10 minutos.
Comentários
01. Resposta: D
Comparando- se cada grandeza com aquela onde está o x.
m² varredores horas
6000--------------18-------------- 5

68
7500--------------15--------------- x
Quanto mais a área, mais horas (diretamente proporcionais)
Quanto menos trabalhadores, mais horas (inversamente proporcionais)
5
𝑥
=
6000
7500
∙
15
18
6000 ∙ 15 ∙ 𝑥 = 5 ∙ 7500 ∙ 18
90000𝑥 = 675000
𝑥 = 7,5 ℎ𝑜𝑟𝑎𝑠
Como 0,5 h equivale a 30 minutos, logo o tempo será de 7 horas e 30 minutos.
02. Resposta: D
Operários horas dias área
20-----------------8-------------60-------4800
15----------------10------------80-------- x
Todas as grandezas são diretamente proporcionais, logo:
4800
𝑥
=
20
15
∙
8
10
∙
60
80
20 ∙ 8 ∙ 60 ∙ 𝑥 = 4800 ∙ 15 ∙ 10 ∙ 80
9600𝑥 = 57600000
𝑥 = 6000𝑚²
03. Resposta: B
Temos 10 funcionários inicialmente, com os afastamentos esse número passou para 8. Se eles
trabalham 8 horas por dia, passarão a trabalhar uma hora a mais perfazendo um total de 9 horas, nesta
condições temos:
Funcionários horas dias
10---------------8--------------27
8----------------9-------------- x
Quanto menos funcionários, mais dias devem ser trabalhados (inversamente proporcionais).
Quanto mais horas por dia, menos dias devem ser trabalhados (inversamente proporcionais).
27
𝑥
=
8
10
∙
9
8
→ x.8.9 = 27.10.8 → 72x = 2160 → x = 30 dias.
04. Resposta: C
Transformando o tempo para segundos: 1 min e 15 segundos = 75 segundos
Quanto mais máquinas menor o tempo (flecha contrária) e quanto mais cópias, mais tempo (flecha
mesma posição)
Máquina cópias tempo
1----------------80-----------75 segundos
7--------------3360-----------x
75
𝑥
=
7
1
∙
80
3360
→ x.7.80 = 75.1.3360 → 560x = 252000 → x = 450 segundos
Transformando
1minuto-----60segundos
x-------------450
x = 7,5 minutos = 7 minutos e 30segundos.
05. Resposta: A
Vamos utilizar a Regra de Três Composta:
Operários  horas dias
128 ----------- 6 -------------- 42
x ------------- 8 -------------- 24
Quanto mais operários, menos horas trabalhadas (inversamente)
Quanto mais funcionários, menos dias (inversamente)

69
𝑥
128
=
6
8
∙
42
24
𝑥
128
=
1
8
∙
42
4
𝑥
128
=
1
8
∙
21
2
16𝑥 = 128 ∙ 21
𝑥 = 8 ∙ 21 = 168
168 – 128 = 40 funcionários a mais devem ser contratados.
06. Resposta: E
Fichas Assistentes dias horas
1000 --------------- 16 -------------- 10 ------------ 6
2000 -------------- 10 -------------- x -------------- 8
Quanto mais fichas, mais dias devem ser trabalhados (diretamente proporcionais).
Quanto menos assistentes, mais dias devem ser trabalhados (inversamente proporcionais).
Quanto mais horas por dia, menos dias (inversamente proporcionais).
10
𝑥
=
1000
2000
∙
10
16
.
8
6
10
𝑥
=
80000
192000
80. 𝑥 = 192.10
𝑥 =
1920
80
𝑥 = 24 𝑑𝑖𝑎𝑠
07. Resposta: C
Faremos uma regra de três composta:
Pessoas Kg dias
4 ------------ 13 ------------ 5
5 ------------ 65 ------------ x
Mais pessoas irão levar menos dias para produzir a mesma quantidade de lixo (grandezas
inversamente proporcionais).
Mais quilos de lixo levam mais dias para serem produzidos (grandezas diretamente proporcionais).
5
𝑥
=
5
4
.
13
65
5
𝑥
=
65
260
65.x = 5 . 260
x = 1300 / 65
x = 20 dias
08. Resposta: C
Faremos uma regra de três composta:
Trabalhadores Hectares h / dia dias
15 ------------------ 210 ---------------- 7 ----------------- 6
20 ------------------ 480 ---------------- 6 ----------------- x
Mais trabalhadores irão levar menos dias para concluir o trabalho (grandezas inversamente
proporcionais).
Mais hectares levam mais dias para se concluir o trabalho (grandezas diretamente proporcionais).

70
Menos horas por dia de trabalho serão necessários mais dias para concluir o trabalho (grandezas
inversamente proporcionais).
6
𝑥
=
20
15
.
210
480
.
6
7
6
𝑥
=
25200
50400
25200.x = 6. 50400 → x = 302400 / 25200 → x = 12 dias
09. Resposta: B
caixas clientes minutos
2 ----------------- 6 ----------- 10
5 ----------------- 45 ----------- x
Quanto mais caixas, menos minutos levará para o atendimento (inversamente proporcionais).
Quanto mais clientes, mais minutos para o atendimento (diretamente proporcionais).
10
𝑥
=
5
2
∙
6
45
10
𝑥
=
30
90
30. 𝑥 = 90.10 𝑥 =
900
30
𝑥 = 30 𝑚𝑖𝑛𝑢𝑡𝑜𝑠
PORCENTAGEM
Razões de denominador 100 que são chamadas de razões centesimais ou taxas percentuais ou
simplesmente de porcentagem9. Servem para representar de uma maneira prática o "quanto" de um
"todo" se está referenciando.
Costumam ser indicadas pelo numerador seguido do símbolo % (Lê-se: “por cento”).
𝒙% =
𝒙
𝟏𝟎𝟎
Exemplos:
01. A tabela abaixo indica, em reais, os resultados das aplicações financeiras de Oscar e Marta entre
02/02/2013 e 02/02/2014.
Notamos que a razão entre os rendimentos e o saldo em 02/02/2013 é:
50
500
, 𝑝𝑎𝑟𝑎 𝑂𝑠𝑐𝑎𝑟, 𝑛𝑜 𝐵𝑎𝑛𝑐𝑜 𝐴;
50
400
, 𝑝𝑎𝑟𝑎 𝑀𝑎𝑟𝑡𝑎, 𝑛𝑜 𝐵𝑎𝑛𝑐𝑜 𝐵.
Quem obteve melhor rentabilidade?
Resolução:
Uma das maneiras de compará-las é expressá-las com o mesmo denominador (no nosso caso o 100),
para isso, vamos simplificar as frações acima:
9IEZZI, Gelson – Fundamentos da Matemática – Vol. 11 – Financeira e Estatística Descritiva
http://www.porcentagem.org
http://www.infoescola.com

71
𝑂𝑠𝑐𝑎𝑟 ⇒
50
500
=
10
100
, = 10%
𝑀𝑎𝑟𝑡𝑎 ⇒
50
400
=
12,5
100
, = 12,5%
Com isso podemos concluir que Marta obteve uma rentabilidade maior que Oscar ao investir no Banco
B.
Uma outra maneira de expressar será apenas dividir o numerador pelo denominador, ou seja:
𝑂𝑠𝑐𝑎𝑟 ⇒
50
500
= 0,10 = 10%
𝑀𝑎𝑟𝑡𝑎 ⇒
50
400
= 0,125 = 12,5%
02. Em uma classe com 30 alunos, 18 são rapazes e 12 são moças. Qual é a taxa percentual de
rapazes na classe?
Resolução:
A razão entre o número de rapazes e o total de alunos é
18
30
. Devemos expressar essa razão na forma
centesimal, isto é, precisamos encontrar x tal que:
18
30
=
𝑥
100
⟹ 𝑥 = 60
E a taxa percentual de rapazes é 60%. Poderíamos ter divido 18 por 30, obtendo:
18
30
= 0,60(. 100%) = 60%
Lucro e Prejuízo
É a diferença entre o preço de venda e o preço de custo.
Caso a diferença seja positiva, temos o lucro(L), caso seja negativa, temos prejuízo(P).
Lucro (L) = Preço de Venda (V) – Preço de Custo (C).
Podemos ainda escrever:
C + L = V ou L = V - C
P = C – V ou V = C - P
A forma percentual é:
Exemplos:
01. Um objeto custa R$ 75,00 e é vendido por R$ 100,00. Determinar:
a) a porcentagem de lucro em relação ao preço de custo;
b) a porcentagem de lucro em relação ao preço de venda.
Resolução:
Preço de custo + lucro = preço de venda → 75 + lucro =100 → Lucro = R$ 25,00
𝑎)
𝑙𝑢𝑐𝑟𝑜
𝑝𝑟𝑒ç𝑜 𝑑𝑒 𝑐𝑢𝑠𝑡𝑜
. 100% ≅ 33,33% 𝑏)
𝑙𝑢𝑐𝑟𝑜
𝑝𝑟𝑒ç𝑜 𝑑𝑒 𝑣𝑒𝑛𝑑𝑎
. 100% = 25%

72
02. O preço de venda de um bem de consumo é R$ 100,00. O comerciante tem um ganho de 25%
sobre o preço de custo deste bem. O valor do preço de custo é:
A) R$ 25,00
B) R$ 70,50
C) R$ 75,00
D) R$ 80,00
E) R$ 125,00
Resolução:
𝐿
𝐶
. 100% = 25% ⇒ 0,25 , o lucro é calculado em cima do Preço de Custo(PC).
C + L = V → C + 0,25. C = V → 1,25. C = 100 → C = 80,00
Resposta D
Aumento e Desconto Percentuais
A) Aumentar um valor V em p%, equivale a multiplicá-lo por (𝟏 +
𝒑
𝟏𝟎𝟎
).V .
Logo:
VA = (𝟏 +
𝒑
𝟏𝟎𝟎
).V
Exemplos:
01. Aumentar um valor V de 20%, equivale a multiplicá-lo por 1,20, pois:
(1 +
20
100
).V = (1+0,20).V = 1,20.V
02. Aumentar um valor V de 200%, equivale a multiplicá-lo por 3, pois:
(1 +
200
100
).V = (1+2).V = 3.V
03. Aumentando-se os lados a e b de um retângulo de 15% e 20%, respectivamente, a área do
retângulo é aumentada de:
(A)35%
(B)30%
(C)3,5%
(D)3,8%
(E) 38%
Resolução:
Área inicial: a.b
Com aumento: (a.1,15).(b.1,20) → 1,38.a.b da área inicial. Logo o aumento foi de 38%.
Logo, alternativa E.
B) Diminuir um valor V em p%, equivale a multiplicá-lo por (𝟏 −
𝒑
𝟏𝟎𝟎
).V.
Logo:
V D = (𝟏 −
𝒑
𝟏𝟎𝟎
).V
Exemplos:
01. Diminuir um valor V de 20%, equivale a multiplicá-lo por 0,80, pois:
(1 −
20
100
). V = (1-0,20). V = 0, 80.V
02. Diminuir um valor V de 40%, equivale a multiplicá-lo por 0,60, pois:
(1 −
40
100
). V = (1-0,40). V = 0, 60.V
03. O preço do produto de uma loja sofreu um desconto de 8% e ficou reduzido a R$ 115,00. Qual
era o seu valor antes do desconto?
Temos que V D = 115, p = 8% e V =? é o valor que queremos achar.

73
V D = (1 −
𝑝
100
). V → 115 = (1-0,08).V → 115 = 0,92V → V = 115/0,92 → V = 125
O valor antes do desconto é de R$ 125,00.
A esse valor final de (𝟏 +
𝒑
𝟏𝟎𝟎
) ou (𝟏 −
𝒑
𝟏𝟎𝟎
), é o que chamamos de fator de multiplicação, muito útil
para resolução de cálculos de porcentagem. O mesmo pode ser um acréscimo ou decréscimo no
valor do produto.
Abaixo a tabela com alguns fatores de multiplicação:
Aumentos e Descontos Sucessivos
São valores que aumentam ou diminuem sucessivamente. Para efetuar os respectivos descontos ou
aumentos, fazemos uso dos fatores de multiplicação.
Vejamos alguns exemplos:
01. Dois aumentos sucessivos de 10% equivalem a um único aumento de...?
Utilizando VA = (1 +
𝑝
100
).V → V. 1,1, como são dois de 10% temos → V. 1,1 . 1,1 → V. 1,21
Analisando o fator de multiplicação 1,21; concluímos que esses dois aumentos significam um único
aumento de 21%.
Observe que: esses dois aumentos de 10% equivalem a 21% e não a 20%.
02. Dois descontos sucessivos de 20% equivalem a um único desconto de:
Utilizando VD = (1 −
𝑝
100
).V → V. 0,8 . 0,8 → V. 0,64 . . Analisando o fator de multiplicação 0,64,
observamos que esse percentual não representa o valor do desconto, mas sim o valor pago com o
desconto. Para sabermos o valor que representa o desconto é só fazermos o seguinte cálculo:
100% - 64% = 36%
Observe que: esses dois descontos de 20% equivalem a 36% e não a 40%.
03. Certo produto industrial que custava R$ 5.000,00 sofreu um acréscimo de 30% e, em seguida,
um desconto de 20%. Qual o preço desse produto após esse acréscimo e desconto?
Utilizando VA = (1 +
𝑝
100
).V para o aumento e VD = (1 −
𝑝
100
).V, temos:
VA = 5000 .(1,3) = 6500 e VD = 6500 .(0,80) = 5200, podemos, para agilizar os cálculos, juntar tudo
em uma única equação:
5000 . 1,3 . 0,8 = 5200
Logo o preço do produto após o acréscimo e desconto é de R$ 5.200,00
Questões
01. (MPE/GO – Auxiliar Administrativo – MPE/GO/2018) João e Miguel são filhos de Pedro e
recebem pensão alimentícia do pai no percentual de 20% sobre o seu salário, cada um. Considerando
que os rendimentos de Pedro são de R$ 2.400,00 mensais, quantos reais sobram para Pedro no final do
mês?
(A) R$ 1.510,00
(B) R$ 1.920,00
(C) R$ 960,00

74
(D) R$ 1.440,00
(E) R$ 480,00
02. (MPE/GO – Secretário Auxiliar – MPE/GO/2018) Joana foi trazer compras. Encontrou um vestido
de 150 reais. Descobriu que se pagasse à vista teria um desconto de 35%. Depois de muito pensar, Joana
pagou à vista o tal vestido.
Quanto ela pagou?
(A) 120,00 reais;
(B) 112,50 reais
(C) 127,50 reais.
(D) 97,50 reais.
(E) 95,00 reais.
03. (SABESP – Agente de Saneamento Ambiental – FCC/2018) O preço de um automóvel, à vista,
é de R$ 36.000,00 e um certo financiamento permite que esse mesmo automóvel seja pago em 18
parcelas mensais idênticas de R$ 2.200,00. Sendo assim, optando por financiar a compra do automóvel,
o valor total a ser pago pelo automóvel, em relação ao preço à vista, aumentará em
(A) 20%.
(B) 12%.
(C) 10%.
(D) 15%.
(E) 22%.
04. (SANEAGO/GO – Agente de Saneamento – UFG/2018) As vendas de Natal em 2017 nos
shopping centers cresceram 6% em relação a 2016, movimentando R$ 51,2 bilhões [O Estado de S.
Paulo, 27/12/2017, p. B1]. De acordo com essas informações, o valor movimentado, em bilhões, pelos
shopping centers com as compras de Natal em 2016 foi, aproximadamente, de
(A) R$ 45,13
(B) R$ 48,20
(C) R$ 48,30
(D) R$ 50,14
05. (SEAD/AP – Assistente Administrativo – FCC/2018) Em uma empresa, o departamento de
recursos humanos fez um levantamento a respeito do número de dependentes de cada funcionário e
organizou os resultados na seguinte tabela:
A porcentagem dos funcionários que têm exatamente um dependente é igual a
(A) 60%.
(B) 40%.
(C) 50%.
(D) 33%.
(E) 66%.
06. (LIQUIGÁS – Assistente Administrativo – CESGRANRIO/2018) Um comerciante comprou
algumas geladeiras, ao preço unitário de R$ 1.550,00, e conseguiu vender apenas algumas delas. Em
cada geladeira vendida, o comerciante obteve um lucro de 16% sobre o preço de compra, e o lucro total
obtido com todas as geladeiras vendidas foi de R$ 26.040,00.
Quantas geladeiras o comerciante vendeu?
(A) 15
(B) 45
(C) 75
(D) 105
(E) 150

75
07. (Câm. de Chapecó/SC – Assistente de Legislação e Administração – OBJETIVA) Em
determinada loja, um sofá custa R$ 750,00, e um tapete, R$ 380,00. Nos pagamentos com cartão de
crédito, os produtos têm 10% de desconto e, nos pagamentos no boleto, têm 8% de desconto. Com base
nisso, realizando-se a compra de um sofá e um tapete, os valores totais a serem pagos pelos produtos
nos pagamentos com cartão de crédito e com boleto serão, respectivamente:
(A) R$ 1.100,00 e R$ 1.115,40.
(B) R$ 1.017,00 e R$ 1.039,60.
(C) R$ 1.113,00 e R$ 1.122,00.
(D) R$ 1.017,00 e R$ 1.010,00.
08. (UFPE - Assistente em Administração – COVEST) Uma loja compra televisores por R$ 1.500,00
e os revende com um acréscimo de 40%. Na liquidação, o preço de revenda do televisor é diminuído em
35%. Qual o preço do televisor na liquidação?
(A) R$ 1.300,00
(B) R$ 1.315,00
(C) R$ 1.330,00
(D) R$ 1.345,00
(E) R$ 1.365,00
09. (Câmara de São Paulo/SP – Técnico Administrativo – FCC) O preço de venda de um produto,
descontado um imposto de 16% que incide sobre esse mesmo preço, supera o preço de compra em 40%,
os quais constituem o lucro líquido do vendedor. Em quantos por cento, aproximadamente, o preço de
venda é superior ao de compra?
(A) 67%.
(B) 61%.
(C) 65%.
(D) 63%.
(E) 69%.
10. (PM/SE – Soldado 3ª Classe – FUNCAB) Numa liquidação de bebidas, um atacadista fez a
seguinte promoção:
Cerveja em lata: R$ 2,40 a unidade.
Na compra de duas embalagens com 12 unidades cada, ganhe 25% de desconto no valor da segunda
embalagem.
Alexandre comprou duas embalagens nessa promoção e revendeu cada unidade por R$3,50. O lucro
obtido por ele com a revenda das latas de cerveja das duas embalagens completas foi:
(A) R$ 33,60
(B) R$ 28,60
(C) R$ 26,40
(D) R$ 40,80
(E) R$ 43,20
11. (Pref. Maranguape/CE – Prof. de educação básica – GR Consultoria e Assessoria) Marcos
gastou 30% de 50% da quantia que possuía e mais 20% do restante. A porcentagem que lhe sobrou do
valor, que possuía é de:
(A) 58%
(B) 68%
(C) 65%
(D) 77,5%
Comentários
01. Resposta: D
Para resolver esta questão devemos encontrar 20% do salário de Pedro, ou seja:
2.400,00 x 20% = 2400 x 0,20 = 480,00
que é o valor que ele paga de pensão, mas como são 2 filhos será 480 + 480 = 960,00, portanto o
valor que ele recebe será de 2400 – 960 = 1440,00.

76
02. Resposta: D
Vamos calcular quanto representa 35% de 150 reais.
150 x 0,35 = 52,50 (é o valor do desconto)
Logo o valor do vestido à vista será de: 150,00 – 52,50 = 97,50.
03. Resposta: C
Primeiramente vamos encontrar o valor o automóvel financiado em 18 parcelas de 2.200:
18 x 2.200 = 39.600.
Agora basta fazermos uma regra de três simples onde o valor à vista de 36.000,00 será os 100% e do
resultado o que aumentar além dos 100% será o valor da porcentagem de acréscimo.
36000 ---- 100
39600 ---- x
36000x = 39600 . 100
36000x = 3960000
x =
3960000
36000
= 110
Assim o valor financiado passou a ser 110%, logo o aumento foi de 110 – 100 = 10%
04. Resposta: C
Primeiramente devemos saber que 51,2 bilhões já está com o aumento de 6% então ele representa
106%, agora basta descobrir o valor ante do aumento, através de uma regra de três simples.
51,2 ---- 106
x ---- 100
106x = 51,2 . 100
106x = 5120
x =
5120
106
= 48,30 aproximadamente.
05. Resposta: B
Aqui devemos ficar atentos pois existe uma pegadinha, observe que o número de funcionários que têm
um ou mais dependentes é de 15, e na outra coluna o número de funcionários que têm dois ou mais
dependentes é de 5, assim estes 5 já estão inclusos nos 5, portanto o total de funcionários será 10 + 15
= 25 e também temos que o número de funcionários que terão apenas 1 dependente será 15 – 5 = 10
funcionários.
Vamos agora encontrar a porcentagem dos funcionários que têm exatamente um dependente:
10
25
= 0,40 = 40%
06. Resposta: D
O primeiro passo é saber quanto que o comerciante lucra por geladeira, com ele lucra 16%, basta
encontrar 16% de 1550.
0,16 x 1550 = 248
Assim o valor que ele lucra por geladeira será 248, mas 26040 foi o valor total de lucro, portanto para
saber quantas geladeiras ele vendeu devemos dividir o lucro total pelo lucro de uma geladeira.
26040
248
= 105
Vendeu 105 geladeiras no total.
07. Resposta: B
Vamos encontrar o valor pago pelo sofá e pelo tapete em cada uma das formas de pagamento:
Cartão de crédito:
10
100
(750 + 380) = 0,10 . 1130 = 113
1130 – 113 = R$ 1017,00
Boleto:
8
100
. (750 + 380) = 0,08 . 1130 = 90,4
1130 – 90,4 = R$ 1039,60

77
08. Resposta: E
Vamos encontrar o preço que ele revende e depois dar o desconto sob esse preço de revenda.
Preço de revenda: 1500 + 40% = 1500 + 1500 x 0,40 = 1500 + 600 = 2100
Preço com desconto: 2100 – 35% =2100 – 0,35 x 2100 = 2100 – 735 = R$ 1365,00
09. Resposta: A
Preço de venda: V
Preço de compra: C
V – 0,16V = 1,4C
0,84V = 1,4C
𝑉
𝐶
=
1,4
0,84
= 1,67
O preço de venda é 67% superior ao preço de compra.
10. Resposta: A
Vamos encontrar o valor da primeira embalagem:
2,40 . 12 = 28,80
Agora como tem desconto de 25% na segunda embalagem, vamos encontrar seu valor (100% - 25%
= 75%):
28,80. 0,75 = 21,60
O total que ele gastou foi de
28,80 + 21,60 = 50,40
Como ele revendeu cada lata por 3,50 ele terá recebido um total de:
3,50 x 24 = 84,00
O lucro então foi de:
R$ 84,00 – R$ 50,40 = R$ 33,60
11. Resposta: B
De um total de 100%, temos que ele gastou 30% de 50% = 30%.50% = 15% foi o que ele gastou,
sobrando: 100% - 15% = 85%. Desses 85% ele gastou 20%, logo 20%.85% = 17%, sobrando:
85% - 17% = 68%.
ÁLGEBRA DAS PROPOSIÇÕES OU LÓGICA PROPOSICIONAL
Caro(a) candidato(a), para que você possa entender o conteúdo de Álgebra das Proposições (ou
Lógica Proposicional), é necessário ficar atento a alguns itens que estão diretamente relacionados,
muito abordado em concursos.
Lógica Proposicional é formada por combinação das proposições, que utiliza conectivos lógicos e
um sistema de regras de derivação.
Para isso é necessário estudarmos conceitos de proposições (simples ou atômicas, abertas ou
fechadas, etc.), tabela verdade, os operadores lógicos e suas propriedades, implicações lógicas.
Portanto é um amplo conhecimento necessário, assim sendo, esse assunto você poderá encontrar
nos conceitos apresentados em nosso material.
ESTRUTURAS LÓGICAS
A lógica pela qual conhecemos hoje foi definida por Aristóteles, constituindo-a como uma ciência
autônoma que se dedica ao estudo dos atos do pensamento (Conceito, Juízo, Raciocínio, Demonstração)
do ponto de vista da sua estrutura ou forma lógica, sem ter em conta qualquer conteúdo material.
4 - Lógica proposicional.

78
A lógica matemática (ou lógica formal) estuda a lógica segundo a sua estrutura ou forma. As estruturas
lógicas consistem em um sistema dedutivo de enunciados, que tem como objetivo criar um grupo de leis
e regras para determinar a validade dos raciocínios. Assim, um raciocínio é considerado válido se é
possível alcançar uma conclusão verdadeira a partir de premissas verdadeiras.
O estudo das estruturas lógicas10
, consiste em aprendermos a associar determinada proposição ao
conectivo correspondente. Mas é necessário aprendermos alguns conceitos importantes para o
aprendizado.
Conceito de Proposição
Chama-se proposição todo o conjunto de palavras ou símbolos que expressam um pensamento ou
uma ideia de sentido completo. Assim, as proposições transmitem pensamentos, isto é, afirmam,
declaram fatos ou exprimem juízos que formamos a respeito de determinados conceitos ou entes.
Elas devem possuir além disso:
- um sujeito e um predicado;
- deve sempre ser possível atribuir um valor lógico: verdadeiro (V) ou falso (F).
Preenchendo esses requisitos estamos diante de uma proposição.
Exemplos
A) Júpiter é o maior planeta do sistema Solar
Analisando temos:
- Quem é o maior planeta do sistema Solar? Júpiter, logo tem um sujeito e um predicado;
- É uma frase declarativa (a frase informa ou declara alguma coisa);
- Podemos atribuir um valor lógico V ou F, independente da questão em si.
B) Salvador é a capital do Brasil.
- Quem é a capital do Brasil? Salvador (atenção, não estamos aqui para julgar), logo tem um sujeito e
um predicado;
C) Todos os músicos são românticos.
- Quem são românticos? Todos os músicos, logo tem um sujeito e um predicado;
Princípios Fundamentais da Lógica
A Lógica matemática adota como regra fundamental três princípios11
(ou axiomas):
I – PRINCÍPIO DA IDENTIDADE: uma proposição verdadeira é verdadeira; uma proposição
falsa é falsa.
II – PRINCÍPIO DA NÃO CONTRADIÇÃO: uma proposição não pode ser verdadeira E falsa
ao mesmo tempo.
III – PRINCÍPIO DO TERCEIRO EXCLUÍDO: toda proposição OU é verdadeira OU é falsa,
verificamos sempre um desses casos, NUNCA existindo um terceiro caso.
Se os princípios acimas não puderem ser aplicados, NÃO podemos classificar uma frase como
proposição.
10
CABRAL, L. C. D.; NUNES, M. C. de A. Raciocínio lógico passo a passo. Rio de Janeiro. Elsevier, 2013.
ALENCAR FILHO, E. de. Iniciação a lógica matemática. São Paulo. Nobel, 2002.
11
Algumas bibliografias consideram apenas dois axiomas o II e o III.

79
Valores Lógicos das Proposições
Chamamos de valor lógico de uma proposição: a verdade, se a proposição for verdadeira (V), e a
falsidade, se a proposição for falsa (F). Designamos as letras V e F para abreviarmos os valores lógicos
verdade e falsidade respectivamente.
Consideremos as seguintes proposições e os seus respectivos valores lógicos:
a) A velocidade de um corpo é inversamente proporcional ao seu tempo. (V)
b) A densidade da madeira é maior que a densidade da água. (F)
A maioria das proposições são proposições contingenciais, ou seja, dependem do contexto para sua
análise. Assim, por exemplo, se considerarmos a proposição simples:
“Existe vida após a morte”, ela poderá ser verdadeira ou falsa, não importa no que nós pensamos, o
que importa é que pode ser atribuído um valor lógico que será verdadeiro ou falso.
Classificação das Proposições
As proposições podem ser classificadas em:
I - Proposições simples (ou atômicas): são formadas por uma única oração, sem conectivos, ou seja,
elementos de ligação.
Exemplos
O céu é azul.
Hoje é sábado.
II - Proposições compostas (ou moleculares): possuem elementos de ligação (conectivos) que ligam
as orações, podendo ser duas, três, e assim por diante.
Exemplos
O ceu é azul ou cinza.
Se hoje é sábado, então vou à praia e jogo futebol.
Observação: os termos em destaque são alguns dos conectivos (termos de ligação) que utilizamos
em lógica matemática.
Sentença aberta
Quando não se pode atribuir um valor lógico verdadeiro ou falso para ela (ou valorar a proposição!),
portanto, não é considerada frase lógica. São consideradas sentenças abertas:
a) Frases interrogativas: Quando será prova? - Estudou ontem? – Fez Sol ontem?
b) Frases exclamativas: Gol! – Que maravilhoso!
c) Frase imperativas: Estude e leia com atenção. – Desligue a televisão.
d) Frases sem sentido lógico (expressões vagas, paradoxais, ambíguas, ...): “esta frase é falsa”
(expressão paradoxal); O cavalo do meu vizinho morreu (expressão ambígua); y + 6 = 4 (se y = - 2 é
verdadeira, mas se y for igual a qualquer outro valor, será falsa e uma proposição não pode ser verdadeira
e falsa ao mesmo tempo, princípio da não contradição).
Proposição (sentença) fechada
Quando a proposição admitir um único valor lógico, seja ele verdadeiro ou falso, nesse caso, será
considerada uma frase, proposição ou sentença lógica.

80
Questões
01. (TJ/PR – Técnico Judiciário – CESPE/2019) Considere as seguintes sentenças.
I A ouvidoria da justiça recebe críticas e reclamações relacionadas ao Poder Judiciário do estado.
II Nenhuma mulher exerceu a presidência do Brasil até o ano 2018.
III Onde serão alocados os candidatos aprovados no concurso para técnico judiciário do TJ/PR?
Assinale a opção correta.
(A) Apenas a sentença I é proposição.
(B) Apenas a sentença III é proposição.
(C) Apenas as sentenças I e II são proposições.
(D) Apenas as sentenças II e III são proposições.
(E) Todas as sentenças são proposições.
02. (CEEE/RS – Técnico em Enfermagem do Trabalho – FUNDATEC/2019) Lista de símbolos:
⇒ Condicional
⇔ Bicondicional
∧ Conector “e”
∨ Conector “ou”
⊻ Conector “ou” exclusivo
¬ Negação da proposição
Assinale a alternativa que apresenta um exemplo de proposição simples.
(A) João é alto e Maria é baixa
(B) Qual é o horário da missa?
(C) Se João estuda, então Maria passa no concurso.
(D) Dois é um número par se e somente se dez é um número ímpar.
(E) Florianópolis é a capital do estado de Santa Catarina.
03. (Pref. de Guarulhos/SP – Inspetor Fiscal de Rendas – VUNESP/2019) Dentre as sentenças a
seguir, aquela que é uma sentença aberta é
(A) 3 ⋅ x + 4 – x – 3 – 2 ⋅ x = 0
(B) 7 + 3 = 11
(C) 0 ⋅ x = 5
(D) 13 ⋅ x = 7
(E) 43 – 1 = 42
04. (FDSBC – Oficial Administrativo – QUADRIX/2019) Das frases a seguir, a única que representa
uma proposição é:
(A) Ronaldo, venha até aqui, por favor.
(B) Que tarde agradável!
(C) Sim.
(D) Maria preparou os documentos.
(E) Onde estão os documentos?
05. (PM/RR – Soldado da Polícia Militar – UERR) Uma sentença aberta pode ser transformada numa
proposição se for atribuído valor a uma variável. Dada a sentença aberta p(y): y2
> 10, assinale o valor a
ser atribuído para tornar a proposição p(y) verdadeira:
DICA: Tire esse PESO de você!
P: Perguntas;
E: Exclamações;
S: Sem sentido;
O: Ordem.
Não são consideradas proposições.

81
(A) x = 4
(B) y = -2
(C) y = 1
(D) x = 0
(E) y = 5
Comentários
01. Resposta: C
I A ouvidoria da justiça recebe críticas e reclamações relacionadas ao Poder Judiciário do estado. É
PROPOSIÇÃO.
II Nenhuma mulher exerceu a presidência do Brasil até o ano 2018. É PROPOSIÇÃO.
III Onde serão alocados os candidatos aprovados no concurso para técnico judiciário do TJ/PR? NÃO
É UMA PROPOSIÇÃO, pois é uma pergunta.
02. Resposta: E
(A) João é alto e Maria é baixa (proposição composta ligada pelo conectivo “e” conjunção)
(B) Qual é o horário da missa? (Não é proposição, pois é uma pergunta)
(C) Se João estuda, então Maria passa no concurso. (proposição composta ligada pelo conectivo
se...então... condicional)
(D) Dois é um número par se e somente se dez é um número ímpar. (proposição composta ligada pelo
conectivo ...se, e somente se... bicondicional)
(E) Florianópolis é a capital do estado de Santa Catarina. (é uma proposição simples)
03. Resposta: D
(A) 3 ⋅ x + 4 – x – 3 – 2 ⋅ x = 0 (simplificando esta expressão teremos 0x + 1 = 0, logo será sentença
fechada, pois qualquer que seja o valor para x, teremos sempre uma mesma resposta)
(B) 7 + 3 = 11 (é uma sentença fechada, pois podemos assumir apenas um valor, F ou V)
(C) 0 ⋅ x = 5 (é uma sentença fechada, pois qualquer que seja o valor de x, sempre podemos atribuir a
mesma resposta, logo podemos valorar em V ou em F)
(D) 13 ⋅ x = 7 (não é uma sentença fechada, pois um valor gera V e qualquer outro valor gera uma F)
(E) 43 – 1 = 42 (é uma sentença fechada, pois podemos assumir apenas um valor, F ou V.)
04. Resposta: D
(A) Ronaldo, venha até aqui, por favor. (Uma ordem, não é proposição)
(B) Que tarde agradável! (Exclamação, não é uma proposição)
(C) Sim. (não é proposição, não possui nem verbo)
(D) Maria preparou os documentos. (É uma proposição, pois possui sentido e verbo, podendo atribuir
V ou F)
(E) Onde estão os documentos? (É uma pergunta, logo não é proposição)
05. Resposta: E
Analisando as alternativas:
A) x = 4, errado pois não temos a variável x.
B) y = -2, errado, pois −22
= 4 < 10
C) y = 1, errado, pois 12
= 1 < 10
D) x = 0, não temos a variável x.
E) y = 5, correto. 52
= 25 > 10
Conceito de Tabela Verdade
É uma forma usual de representação das regras da Álgebra Booleana. Nela, é representada cada
proposição (simples ou composta) e todos os seus valores lógicos possíveis. Partimos do Princípio do
Terceiro Excluído, toda proposição simples é verdadeira ou falsa , tendo os valores lógicos V (verdade)
ou F (falsidade).
Quando trabalhamos com as proposições compostas, determinamos o seu valor lógico partindo das
proposições simples que a compõe.

82
Número de Linhas de uma Tabela Verdade
“A tabela verdade de uma proposição composta com n* proposições simples componentes
contém 2n
linhas.” (* Algumas bibliografias utilizam o “p” no lugar do “n”)
Os valores lógicos “V” e “F” se alteram de dois em dois para a primeira proposição “p” e de um em um
para a segunda proposição “q”, em suas respectivas colunas, e, além disso, VV, VF, FV e FF, em cada
linha, são todos os arranjos binários com repetição dos dois elementos “V” e “F”, segundo ensina a Análise
Combinatória.
Construção da tabela verdade de uma proposição composta
Vamos começar contando o número de proposições simples que a integram. Se há n proposições
simples componentes, então temos 2n
linhas. Feito isso, atribuimos a 1ª proposição simples “p1” 2n
/ 2 =
2n -1
valores V , seguidos de 2n – 1
valores F, e assim por diante.
Exemplos
1) Se tivermos 2 proposições temos que 2n
=22
= 4 linhas e 2n – 1
= 22 - 1
= 2, temos para a 1ª proposição
2 valores V e 2 valores F se alternam de 2 em 2 , para a 2ª proposição temos que os valores se alternam
de 1 em 1 (ou seja metade dos valores da 1ª proposição). Observe a ilustração, a primeira parte dela
corresponde a árvore de possibilidades e a segunda a tabela propriamente dita.
(Fonte: http://www.colegioweb.com.br/nocoes-de-logica/tabela-verdade.html)
2) Se tivermos 3 proposições simples, fazendo os cálculos temos: 2n
=23
= 8 linhas e 2n – 1
= 23 - 1
= 4,
temos para a 1ª proposição 4 valores V e 4 valores F se alternam de 4 em 4 , para a 2ª proposição temos
que os valores se alternam de 2 em 2 (metade da 1ª proposição) e para a 3ª proposição temos valores
que se alternam de 1 em 1(metade da 2ª proposição).
ATENÇÃO:
O valor lógico de qualquer proposição composta depende UNICAMENTE dos
valores lógicos das proposições simples componentes, ficando por eles
UNIVOCAMENTE determinados.

83
(Fonte: http://www.colegioweb.com.br/nocoes-de-logica/tabela-verdade.html)
Estudo dos Operadores e Operações Lógicas (Conectivos Lógicos)
Quando efetuamos certas operações sobre proposições chamadas operações lógicas, efetuamos
cálculos proposicionais, semelhantes a aritmética sobre números, de forma a determinarmos os valores
das proposições.
1) Negação ( ~ ): chamamos de negação de uma proposição representada por “não p” cujo valor lógico
é verdade (V) quando p é falsa e falsidade (F) quando p é verdadeira. Assim “não p” tem valor lógico
oposto daquele de p.
Pela tabela verdade temos:
Exemplos
Na primeira parte da tabela todas as afirmações são verdadeiras, logo ao negarmos os termos passam
a ter como valor lógico a falsidade.
Para negar algo que já possui o “não”, basta retirá-lo.
A negação de “Mário não é palmeirense” será “Mário é palmeirense”.
- Dupla negação (Teoria da Involução): vamos considerar as seguintes proposições primitivas, p:”
Netuno é o planeta mais distante do Sol”; sendo seu valor verdadeiro ao negarmos “p”, vamos obter a
seguinte proposição ~p: “Netuno NÃO é o planeta mais distante do Sol” e negando novamente a
proposição “~p” teremos ~(~p): “NÃO É VERDADE que Netuno NÃO é o planeta mais distante do Sol”,
sendo seu valor lógico verdadeiro (V). Logo, a dupla negação equivale a termos de valores lógicos a sua
proposição primitiva.
p ≡ ~(~p)
2) Conjunção “e” – produto lógico (^): chama-se de conjunção de duas proposições p e q a
proposição representada por “p e q”, cujo valor lógico é verdade (V) quando as proposições, p e q, são
ambas verdadeiras e falsidade (F) nos demais casos.
Simbolicamente temos: “p ^ q” (lê-se: “p E q”).

84
Exemplos
Sejam as seguintes proposições:
p: Carlos é médico; (suponha que seja V)
q: João é dentista; (suponha que seja F)
r: Ricardo é professor; (suponha que seja V)
s: Manoel é jogador de futebol. (suponha que seja F)
I –
p: Carlos é médico;
r: Ricardo é professor;
Carlos é médico e Ricardo é professor.
V e V
Gera uma proposição composta Verdadeira.
II –
Carlos é médico e João é Dentista.
V e F
Gera uma proposição composta Falsa.
III –
Manoel é jogador de futebol e Ricardo é professor.
F e V
IV –
João é dentista e Manoel é jogador de futebol.
F e F
3) Disjunção inclusiva “ou” – soma lógica – disjunção simples (v): chama-se de disjunção
inclusiva de duas proposições p e q a proposição representada por “p ou q”, cujo valor lógico é verdade
(V) quando pelo menos uma das proposições, p e q, é verdadeira e falsidade (F) quando ambas são
falsas.
Simbolicamente: “p v q” (lê-se: “p OU q”).
DICA:
Na conjunção (e), só é Verdade se as duas partes
forem V, caso contrário a conjunção será Falsa.

85
Exemplos
I –
Carlos é médico ou Ricardo é professor.
V ou V
II –
Carlos é médico ou João é Dentista.
V ou F
III –
Manoel é jogador de futebol ou Ricardo é professor.
F ou V
IV –
João é dentista ou Manoel é jogador de futebol.
F ou F
4) Disjunção exclusiva ( v ): chama-se disjunção exclusiva de duas proposições p e q, cujo valor
lógico é verdade (V) somente quando p é verdadeira ou q é verdadeira, mas não quando p e q são
ambas verdadeiras e a falsidade (F) quando p e q são ambas verdadeiras ou ambas falsas.
Simbolicamente: “p v q” (lê-se; “OU p OU q”; “OU p OU q, MAS NÃO AMBOS”).
DICA:
Na disjunção simples (ou), só é Falso se as duas
partes forem F, caso contrário a disjunção simples
será V, ou seja, uma parte sendo V já garante que
ela seja V.

86
Exemplos
I –
OU Carlos é médico ou Ricardo é professor.
Ou V ou V
II –
Ou Carlos é médico ou João é Dentista.
Ou V ou F
III –
OU Manoel é jogador de futebol ou Ricardo é professor.
Ou F ou V
IV –
Ou João é dentista ou Manoel é jogador de futebol.
Ou F ou F
5) Implicação lógica ou condicional (→): chama-se proposição condicional ou apenas condicional
representada por “se p então q”, cujo valor lógico é falsidade (F) no caso em que p é verdade e q é falsa
e a verdade (V) nos demais casos.
Simbolicamente: “p → q” (lê-se: p é condição suficiente para q; q é condição necessária para p).
p é o antecedente e q o consequente e “→” é chamado de símbolo de implicação.
DICA:
Na disjunção exclusiva (ou...ou...), só é Falso se as
duas partes forem F, ou se as duas partes forem V,
ou seja, se as duas partes tiverem o mesmo valor
lógico, o resultado será falso.

87
Exemplos
I –
Se Carlos é médico, então Ricardo é professor.
V → V
II –
Se Carlos é médico, então João é Dentista.
V → F
Gera uma proposição composta FALSA.
III –
Se Manoel é jogador de futebol, então Ricardo é professor.
F → V
IV –
Se João é dentista, então Manoel é jogador de futebol.
F → F
6) Dupla implicação ou bicondicional (↔):chama-se proposição bicondicional ou apenas
bicondicional representada por “p se e somente se q”, cujo valor lógico é verdade (V) quando p e q são
ambas verdadeiras ou ambas falsas e a falsidade (F) nos demais casos.
Simbolicamente: “p ↔ q” (lê-se: p é condição necessária e suficiente para q; q é condição necessária
e suficiente para p).
DICA:
Na condicional (Se...então...), só é Falso se a
primeira parte (antecedente) for V e a segunda parte
(consequente) for F, caso contrário será sempre
Verdadeiro.

88
Exemplos
I –
Carlos é médico se, e somente se Ricardo é professor.
V ↔ V
II –
Carlos é médico se, e somente se João é Dentista.
V ↔ F
III –
Manoel é jogador de futebol se, e somente se Ricardo é professor.
F ↔ V
IV –
João é dentista se, e somente se Manoel é jogador de futebol.
F ↔ F
Transformação da linguagem corrente para a simbólica
Este assunto é muito abordado em provas, ou então, os candidatos(as) acabam utilizando para
resolver as questões de lógica, eu particularmente, sempre transformo para a linguagem simbólica, pois
acredito que facilita a resolução dos exercícios.
DICA:
Na bicondicional (...se, e somente se...), só é
Verdadeiro quando ambas forem iguais (FF ou VV),
se for uma parcela verdadeira e a outra falsa, a
bicondicional será falsa, é o contrário da disjunção
exclusiva.

89
Sejam as seguintes proposições simples denotadas por “p”, “q” e “r” representadas por:
p: Luciana estuda.
q: João bebe.
r: Carlos dança.
Sejam, agora, as seguintes proposições compostas denotadas por: “P”, “Q”, “R”, representadas por:
P: Se Luciana estuda e João bebe, então Carlos não dança.
Q: É falso que João bebe ou Carlos dança, mas Luciana não estuda.
R: Ou Luciana estuda ou Carlos dança se, e somente se, João não bebe.
O primeiro passo é destacarmos os operadores lógicos (modificadores e conectivos) e as proposições.
Depois reescrevermos de forma simbólica, vejamos:
Juntando as informações temos que, P: (p ^ q) → ~r
Continuando:
Q: É falso que João bebe ou Carlos dança, mas Luciana estuda.
Simbolicamente temos: Q: ~ (q v r ^ ~p).
R: Ou Luciana estuda ou Carlos dança se, e somente se, João não bebe.
(p v r) ↔ ~q
Observação: os termos “É falso que”, “Não é verdade que”, “É mentira que” e “É uma falácia que”,
quando iniciam as frases negam, por completo, as frases subsequentes.
O uso de parêntesis
A necessidade de usar parêntesis na simbolização das proposições se deve a evitar qualquer tipo de
ambiguidade, assim na proposição, p ^ q v r, nos dá as seguintes proposições:
(I) (p ^ q) v r - Conectivo principal é da disjunção simples.
(II) p ^ (q v r) - Conectivo principal é da conjunção.
As quais apresentam significados diferentes, pois os conectivos principais de cada proposição
composta dão valores lógicos diferentes como conclusão.
Agora observe a expressão: p ^ q → r v s, dá lugar, colocando parêntesis as seguintes proposições:
a) ((p ^ q) → r) v s
b) p ^ ((q → r) v s)
c) (p ^ (q → r)) v s
d) p ^ (q → (r v s))
e) (p ^ q) → (r v s)
Aqui duas quaisquer delas não tem o mesmo significado. Porém existem muitos casos que os
parêntesis são suprimidos, a fim de simplificar as proposições simbolizadas, desde que, naturalmente,
ambiguidade alguma venha a aparecer. Para isso a supressão do uso de parêntesis se faz mediante a
algumas convenções, das quais duas são particularmente importantes:

90
1ª) A “ordem de precedência” para os conectivos é:
(I) ~ (negação)
(II) ^, v (conjunção “e” ou disjunção simples “ou”, têm a mesma precedência, operando-se o que ocorrer
primeiro, da esquerda para direita).
(III) v (disjunção exclusiva, ou...ou...)
(III) → (condicional, se...então...)
(IV) ↔ (bicondicional, ...se, e somente se...)
Portanto o mais “fraco” é “~” e o mais “forte” é “↔”.
Logo: Os símbolos → e ↔ têm preferência sobre ^ e v.
Exemplos
1) p → q ↔ s ^ r, é uma bicondicional e nunca uma condicional ou uma conjunção. Para convertê-la
numa condicional há que se usar parêntesis:
p →( q ↔ s ^ r )
E para convertê-la em uma conjunção:
(p → q ↔ s) ^ r
2ª) Quando um mesmo conectivo aparece sucessivamente repetido, suprimem-se os
parêntesis, fazendo-se a associação a partir da esquerda.
Segundo estas duas convenções, as duas seguintes proposições se escrevem:
- Outros símbolos para os conectivos (operadores lógicos):
“¬” (cantoneira) para negação (~).
“●” e “&” para conjunção (^).
“‫”ﬤ‬ (ferradura) para a condicional (→).
Em síntese temos a tabela verdade das proposições que facilitará na resolução de diversas questões
(Fonte: http://www laifi.com.)
Exemplo
1) Vamos construir a tabela verdade da proposição:
P(p,q) = ~ (p ^ ~q)
1ª Resolução) Vamos formar o par de colunas correspondentes as duas proposições simples p e q.
Em seguida a coluna para ~q , depois a coluna para p ^ ~q e a útima contendo toda a proposição ~ (p ^
~q), atribuindo todos os valores lógicos possíveis de acordo com os operadores lógicos.

91
2ª Resolução) Vamos montar primeiro as colunas correspondentes a proposições simples p e q ,
depois traçar colunas para cada uma dessas proposições e para cada um dos conectivos que compõem
a proposição composta.
Depois completamos, em uma determinada ordem as colunas escrevendo em cada uma delas os
valores lógicos.
Observe que, vamos preenchendo a tabela com os valores lógicos (V e F), depois resolvemos os
operadores lógicos (modificadores e conectivos) e obtemos em 4 os valores lógicos da proposição que
correspondem a todas possíveis atribuições de p e q.
3ª Resolução) Resulta em suprimir a tabela verdade anterior as duas primeiras da esquerda relativas
às proposições simples componentes p e q. Obtermos então a seguinte tabela verdade simplificada:
ÁLGEBRA DAS PROPOSIÇÕES12
Propriedades da Conjunção
Sendo as proposições p, q e r simples, quaisquer que sejam t e w, proposições também simples, cujos
valores lógicos respectivos são V (verdade) e F (falsidade), temos as seguintes propriedades:
1) Idempotente: p ^ p ⇔ p (o símbolo “⇔” representa equivalência).
A tabela verdade de p ^ p e p, são idênticas, ou seja, a bicondicional p ^ p ↔ p é tautológica.
12
CABRAL, L. C. D.; NUNES, M. C. de A. Raciocínio lógico passo a passo. Rio de Janeiro. Elsevier, 2013.
ALENCAR FILHO, E. de. Iniciação a lógica matemática. São Paulo. Nobel, 2002.

92
2) Comutativa: p ^ q ⇔ q ^ p
A tabela verdade de p ^ q e q ^ p são idênticas, ou seja, a bicondicional p ^ q ↔ q ^ p é tautológica.
3) Associativa: (p ^ q) ^ r ⇔ p ^ (q ^ r)
A tabela verdade de (p ^ q) ^ r e p ^ (q ^ r) são idênticas, ou seja, a bicondicional (p ^ q) ^ r ↔ p ^ (q ^
r) é tautológica.
4) Identidade: p ^ t ⇔ p e p ^ w ⇔ w
A tabela verdade de p ^ t e p, e p ^ w e w são idênticas, ou seja, a bicondicional p ^ t ↔ p e p ^ w ↔ w
são tautológicas.
Estas propriedades exprimem que t e w são respectivamente elemento neutro e elemento absorvente
da conjunção.
Propriedades da Disjunção
Sendo as proposições p, q e r simples, quaisquer que sejam t e w, proposições também simples, cujos
valores lógicos respectivos são V (verdade) e F (falsidade), temos as seguintes propriedades:
1) Idempotente: p v p ⇔ p
A tabela verdade de p v p e p, são idênticas, ou seja, a bicondicional p v p ↔ p é tautológica.
2) Comutativa: p v q ⇔ q v p
A tabela verdade de p v q e q v p são idênticas, ou seja, a bicondicional p v q ↔ q v p é tautológica.

93
3) Associativa: (p v q) v r ⇔ p v (q v r)
A tabela verdade de (p v q) v r e p v (q v r) são idênticas, ou seja, a bicondicional (p v q) v r ↔ p v (q v
r) é tautológica.
4) Identidade: p v t ⇔ t e p v w ⇔ p
A tabela verdade de p v t e p, e p v w e w são idênticas, ou seja, a bicondicional p v t ↔ t e p v w ↔ p
são tautológicas.
Estas propriedades exprimem que t e w são respectivamente elemento absorvente e elemento neutro
da disjunção.
Propriedades da Conjunção e Disjunção
Sejam p, q e r proposições simples quaisquer.
1) Distributiva:
- p ^ (q v r) ⇔ (p ^ q) v (p ^ r)
- p v (q ^ r) ⇔ (p v q) ^ (p v r)
A tabela verdade das proposições p ^ (q v r) e (p v q) ^ (p v r) são idênticas, e observamos que a
bicondicional p ^ (q v r) ↔ (p ^ q) v (p ^ r) é tautológica.
Analogamente temos ainda que a tabela verdade das proposições p v (q ^ r) e (p v q) ^ (p v r) são
idênticas e sua bicondicional p v (q ^ r) ↔ (p v q) ^ (p v r) é tautológica.
A equivalência p ^ (q v r) ↔ (p ^ q) v (p ^ r), exprime que a conjunção é distributiva em relação à
disjunção, e a equivalência p v (q ^ r) ↔ (p v q) ^ (p v r), exprime que a disjunção é distributiva em relação
à conjunção.
Exemplo
“Carlos estuda E Jorge trabalha OU viaja” é equivalente à seguinte proposição:
“Carlos estuda E Jorge trabalha” OU “Carlos estuda E Jorge viaja”.
2) Absorção:
- p ^ (p v q) ⇔ p
- p v (p ^ q) ⇔ p

94
A tabela verdade das proposições p ^ (p v q) e p, ou seja, a bicondicional p ^ (p v q) ↔ p é tautológica.
Analogamente temos ainda que a tabela verdade das proposições p v (p ^ q) e p são idênticas, ou
seja, a bicondicional p v (p ^ q) ↔ p é tautológica.
Sinônimos dos Conectivos Lógicos
Não é tão incomum utilizar alguns sinônimos para os conectivos lógicos, vamos ver alguns deles.
Seja p: João é Dentista, q: João é paulista.
João é dentista, mas é paulista.
João é dentista e paulista.
e = mas (conjunção)
João não é dentista, nem paulista.
João não é dentista e não é paulista.
Nem = e + não
Referências
CABRAL, Luiz Cláudio Durão; NUNES, Mauro César de Abreu - Raciocínio lógico passo a passo – Rio de Janeiro: Elsevier, 2013.
ALENCAR FILHO, Edgar de – Iniciação a lógica matemática – São Paulo: Nobel – 2002.
Questões
01. (DOCAS/PB – Assistente Administrativo – IBFC) Se o valor lógico de uma proposição “P” é
verdade e o valor lógico de uma proposição “Q” é falso, então o valor lógico do bicondicional entre as
duas proposições é:
(A) Falso
(B) Verdade
(C) Inconclusivo
(D) Falso ou verdade
02. (DOCAS/PB – Assistente Administrativo – IBFC) Dentre as alternativas, a única correta é:
(A) O valor lógico da conjunção entre duas proposições é verdade se os valores lógicos das duas
proposições forem falsos.
(B) O valor lógico do bicondicional entre duas proposições é verdade se os valores lógicos das duas
(C) O valor lógico da disjunção entre duas proposições é verdade se os valores lógicos das duas
(D) O valor lógico do condicional entre duas proposições é falso se os valores lógicos das duas
03. (EBSERH – Técnico em Citopatologia – AOCP) Considerando a proposição composta (p ∨ r), é
correto afirmar que
(A) a proposição composta é falsa se apenas p for falsa.
(B) a proposição composta é falsa se apenas r for falsa.

95
(C) para que a proposição composta seja verdadeira é necessário que ambas, p e r sejam verdadeiras.
(D) para que a proposição composta seja verdadeira é necessário que ambas, p e r sejam falsas.
(E) para que a proposição composta seja falsa é necessário que ambas, p e r sejam falsas.
04. (MEC – Conhecimentos básicos para os Postos 9,10,11 e 16 – CESPE)
A figura acima apresenta as colunas iniciais de uma tabela-verdade, em que P, Q e R representam
proposições lógicas, e V e F correspondem, respectivamente, aos valores lógicos verdadeiro e falso.
Com base nessas informações e utilizando os conectivos lógicos usuais, julgue o item subsecutivo.
A última coluna da tabela-verdade referente à proposição lógica P v (Q↔R) quando representada na
posição horizontal é igual a
( ) Certo ( ) Errado
05. (FLAMA/SC – Geólogo – UNESC/2019) Considere verdadeiras as afirmações a seguir:
I - Se Vivi é costureira, então Verônica não é advogada
II - Se Verinha é bailarina, então Verônica é advogada
III - Virna é professora
IV - Ou Verinha é bailarina, ou Virna não é professora.
Com base nessas afirmações podemos concluir corretamente que:
(A) Se Virna é professora, então Verônica não é advogada
(B) Se Verônica não é advogada, então Verinha não é bailarina
(C) Virna é professora e Verônica não é advogada
(D) Verônica não é advogada ou Vivi é costureira
06. (Pref. de Manaus/AM – Assistente Técnico Fazendário – FCC/2019) Aos domingos,
− como pizza no jantar ou não tomo açaí,
− corro ou jogo futebol e
− tomo açaí ou não corro.
Se, no último domingo, não joguei futebol, então
(A) corri e não comi pizza no jantar.
(B) não corri e comi pizza no jantar.
(C) não comi pizza no jantar e não tomei açaí.
(D) não corri e não tomei açaí.
(E) corri e tomei açaí.

96
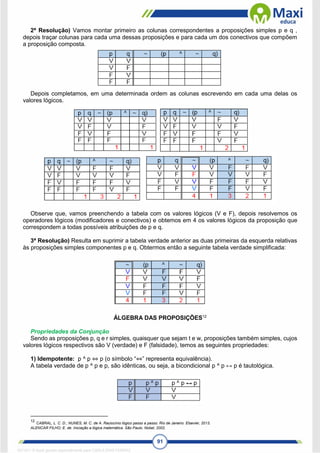
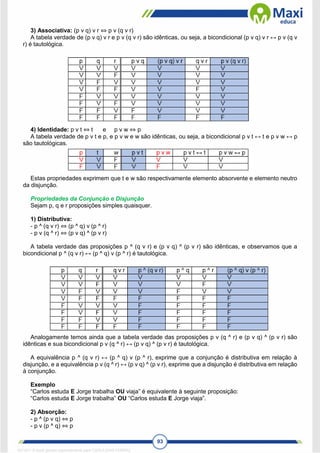
07. (BRDE-Analista de Sistemas, Desenvolvimento de Sistemas – FUNDATEC) Qual operação
lógica descreve a tabela verdade da função Z abaixo cujo operandos são A e B? Considere que V significa
Verdadeiro, e F, Falso.
(A) Ou.
(B) E.
(C) Ou exclusivo.
(D) Implicação (se...então).
(E) Bicondicional (se e somente se).
08. (TCE/SP – Auxiliar da Fiscalização Financeira II – FCC) Considere a afirmação condicional: Se
Alberto é médico ou Alberto é dentista, então Rosa é engenheira.
Seja R a afirmação: 'Alberto é médico';
Seja S a afirmação: 'Alberto é dentista' e
Seja T a afirmação: 'Rosa é engenheira'.
A afirmação condicional será considerada necessariamente falsa quando
(A) R for verdadeira, S for falsa e T for verdadeira.
(B) R for falsa, S for verdadeira e T for verdadeira.
(C) R for falsa, S for falsa e T for falsa.
(D) R for falsa, S for falsa e T for verdadeira.
(E) R for verdadeira, S for falsa e T for falsa.
09. (TER-RJ – Analista Judiciário – CONSULPLAN) De acordo com algumas implicações lógicas,
analise as afirmativas a seguir.
I. Se p é verdadeira e q é verdadeira, então p Λ q é verdadeira.
II. Se p é verdadeira ou q é verdadeira, então p V q é falsa.
III. Se p é verdadeira e p ⟶ q é verdadeira, então q é verdadeira.
IV. Se ~p é verdadeira e p V q é verdadeira, então q é verdadeira.
V. Se ~q é verdadeira e p ⟶ q é verdadeira, então ~p é verdadeira.
VI. Se p V q é verdadeira, p ⟶ r é verdadeira e q ⟶ r é verdadeira, então r é verdadeira.
VII. p V [q Λ (~q)]⇔ p.
VIII. p⟶ q⇔(~p) V p.
Estão INCORRETAS apenas as afirmativas
(A) I e II.
(B) II e VIII.
(C) I, II, VI e VIII.
(D) III, IV, V e VI.
10. (ISGH - Médico Pediatra - Instituto Pró Município) Analise as seguintes proposições:
Proposição I: 4 é número par;
Proposição II: 2 > 5;
Proposição III: 6 é número ímpar.
Qual das proposições abaixo apresenta valor lógico verdadeiro?
(A) Se 2 > 5 e 6 é número ímpar, então 4 é número par;
(B) Se 2 > 5 ou 4 é número par, então 6 é número ímpar;
(C) Se 4 é número par ou 6 é número ímpar, então 2 > 5;
(D) Se 4 é número par, então 2 > 5 ou 6 é número ímpar.

97
11. (Câm. de Indaiatuba/SP – Analista de Sistemas – VUNESP/2018) Considere verdadeiras as
afirmações I e II, e falsa a afirmação III.
I. Se Hugo é policial, então Beatriz é juíza.
II. Se Fernando é vereador, então Vanessa é professora.
III. Beatriz não é juíza ou Vanessa é professora.
A alternativa que contém uma afirmação necessariamente verdadeira, com base nas afirmações
apresentadas é:
(A) Fernando não é vereador
(B) Hugo é policial.
(C) Hugo não é policial e Fernando é vereador.
(D) Hugo é policial e Fernando não é vereador.
(E) Hugo é policial ou Fernando é vereador.
Comentários
01. Resposta: A
Na tabela da bicondicional só será verdadeiro se a primeira parte for igual à segunda, ou seja, VV ou
FF, neste exercício ele pergunta VF, portanto gera uma falsidade.
02. Resposta: B
Vamos relembrar as tabelas verdades.
Conjunção: Só é Verdadeiro se as duas partes forem verdadeiras (VV), caso contrário será FALSA.
Disjunção Simples: Só é Falso se as duas partes forem falsas (FF), caso contrário será VERDADEIRA.
Condicional: Só é Falso se for Verdade na primeira e falsidade na segunda (VF), caso contrário será
VERDADEIRA.
Bicondicional: Só é Verdadeiro se as duas partes forem iguais (VV ou FF), caso contrário será FALSA.
Disjunção Exclusiva: É o contrário da bicondicional, é Falsa quando as duas partes forem iguais (VV
ou FF), caso contrário será VERDADEIRA.
Portanto a alternativa correta é a alternativa B.
03. Resposta: E
O símbolo “v” é da disjunção simples, e ela só é falsa quando as duas proposições que a compõe são
falsas.
04. Resposta: Certo
Precisamos montar a tabela verdade de P v (Q↔R), como a bicondicional está entre parêntesis a
última coluna será da disjunção simples, montando a tabela verdade temos:
No enunciado a última coluna está na horizontal, mas a ordem é idêntica, logo está correta.
05. Resposta: B
III - Virna é professora
Como elas são verdadeiras, procuramos alguma proposição simples ou alguma conjunção, pois só
existe uma possibilidade para elas serem verdadeiras, vamos iniciar pela III - Virna é professora, pois é
uma proposição simples.

98
Agora vamos pela:
Como temos um Ou...ou... para ser verdadeiro sabendo que Virna não é professora é falso, resta que
Verinha é bailarina será verdadeira.
V F
Agora vamos para a II
V V
Verônica é advogada tem que ser verdadeira, pois caso contrário teríamos VF e na condicional isso é
falso, agora vamos para I.
F F
Verônica não é advogada será falso, pois Verônica é advogada era verdadeira, logo Vivi é costureira
precisa ser falsa, senão teríamos um VF e na condicional isso é falso.
Verinha é bailarina – VERDADEIRO
Virna é professora – VERDADEIRO
Verônica é advogada – VERDADEIRO
Vivi é costureira – FALSO
Vamos analisar as alternativas agora:
(A) Se Virna é professora, então Verônica não é advogada
V→F essa condicional é falsa
(B) Se Verônica não é advogada, então Verinha não é bailarina
F → F, essa condicional é verdadeira, logo é a alternativa correta.
(C) Virna é professora e Verônica não é advogada
F e F a conjunção será FALSA
(D) Verônica não é advogada ou Vivi é costureira
F ou F, essa disjunção simples será falsa.
06. Resposta: E
Repare que temos algumas premissas, portanto precisamos encontrar alguma destas premissas que
contenha uma conjunção ou proposição simples, ou iniciar pela informação dada no enunciado, observe:
Se, no último domingo, não joguei futebol, então
Não jogar futebol será V, logo jogar Futebol será F, portanto partiremos daqui, agora utilizaremos a
premissa que fala sobre futebol:
− corro ou jogo futebol
? ou F, para a disjunção simples ser verdadeira o ? precisa obrigatoriamente ser V, logo correr é V.
− tomo açaí ou não corro.
? ou F, repare que para a disjunção simples ser V o ? precisa obrigatoriamente ser V, logo tomo açaí
é V.
− como pizza no jantar ou não tomo açaí,
? ou F, novamente o ? precisa ser V, logo como pizza no jantar é V.
Sendo assim teremos:
Correr: VERDADEIRO
Jogar futebol: VERDADEIRO
Tomar açaí: VERDADEIRO
Comer pizza no jantar: VERDADEIRO
Vamos analisar as alternativas:
(A) corri e não comi pizza no jantar.
V e F, essa conjunção é FALSA.
(B) não corri e comi pizza no jantar.
F e V, essa conjunção é FALSA.
(C) não comi pizza no jantar e não tomei açaí.
F e F, essa conjunção é FALSA.
(D) não corri e não tomei açaí.
F e F, essa conjunção é FALSA.
(E) corri e tomei açaí.
V e V, essa conjunção é VERDADEIRA, logo é a alternativa correta.

99
07. Resposta: D
Como Z é o operador, repare a tabela verdade, só temos 1 caso em que é falso, sendo assim já diminui
nossas possibilidades, repare que no falso, os operandos temos VF e gera F, pensando na tabela
verdade, teríamos uma condicional, vamos exemplificar:
Observe novamente a tabela abaixo, considere A = p, B = q e Z = condicional.
08. Resposta: E
RvS→T
Para a condicional ser falsa, devemos ter:
V→F
Portanto a afirmação (T: Rosa é engenheira) tem que ser falsa.
E para RvS ser verdadeira, as duas só não podem ser falsas.
Lembrando pela tabela verdade de cada uma:
Condicional
Disjunção
Desta forma, T é necessariamente falsa, já R, S só não pode ser ambas falsas, portanto a única
alternativa em que T é falsa e R ou S não são falsas simultaneamente é a alternativa E.
09. Resposta: B
Vamos analisar as informações.
I. Se p é verdadeira e q é verdadeira, então p Λ q é verdadeira.
Verdadeira, pois V e V gera uma verdade
II. Se p é verdadeira ou q é verdadeira, então p V q é falsa.
Na disjunção se uma for verdadeira já basta para a disjunção simples ser verdadeira.
III. Se p é verdadeira e p ⟶ q é verdadeira, então q é verdadeira.
Na condicional, p,q verdadeiras gera p ⟶ q verdadeira, correta.
IV. Se ~p é verdadeira e p V q é verdadeira, então q é verdadeira.
~p é verdadeira, então p é falsa, com isso q é obrigatoriamente verdadeira, logo está correta.
V. Se ~q é verdadeira e p ⟶ q é verdadeira, então ~p é verdadeira.
~q é verdadeira, então q é falsa, mas temos que p ⟶ q é verdadeira, logo p precisa ser falsa, sendo
assim ~p vai ser verdadeira.
Podemos até continuar mostrando cada uma delas, mas apenas com a I sendo verdadeira e II sendo
falsa, a única alternativa que dá certo é a alternativa “B”.
10. Resposta: A
Para solucionar essa questão, basta saber que na condicional (A ⟶ B), sendo B (Verdade) ela será
sempre verdadeira.
Pois na condicional somente é falso quando:
(V ⟶ F = F)
Sabendo disso,
Se 2 > 5 e 6 é número ímpar, então 4 é número par;
Nem precisa fazer ⟶ V = Verdadeiro

100
4 é um número par então será verdadeiro, daí não importa o valor do antecedente (nesse caso 2 > 5
e 6 é número ímpar) a afirmação inteira já vai ser verdadeira.
11. Resposta: A
No enunciado foi dado os valores lógicos das afirmações:
I. Se Hugo é policial, então Beatriz é juíza. VERDADEIRA
II. Se Fernando é vereador, então Vanessa é professora. VERDADEIRA
III. Beatriz não é juíza ou Vanessa é professora. FALSA
Precisamos descobrir o valor lógico de cada uma das proposições simples, vamos começar pela III,
pois para a disjunção simples ser falsa, só tem uma possibilidade, que será ambas falsas, sendo assim
Beatriz não é juíza FALSA
Vanessa é professora FALSA
Agora vamos para a afirmação II.
II. Se Fernando é vereador, então Vanessa é professora
? ⟶ F, logo o ? precisa obrigatoriamente ser Falso, pois II é verdadeiro, sendo assim:
Fernando é vereador FALSA
Vamos analisar a afirmação I.
I. Se Hugo é policial, então Beatriz é juíza.
? ⟶ V, independentemente do valor de ? a condicional sempre será verdadeira, logo não podemos
afirmar nada sobre Hugo é policial.
Portanto:
Beatriz é juíza VERDADEIRO
Vanessa não é professora VERDADEIRO
Fernando não é vereador VERDADEIRO
Hugo é policial – NADA podemos afirmar.
Vamos analisar as afirmativas:
(A) Fernando não é vereador
Verdadeiro, portanto, é a alternativa correta.
(B) Hugo é policial.
Não podemos afirmar.
(C) Hugo não é policial e Fernando é vereador.
? e F, independentemente de Hugo não ser policial, na conjunção se uma proposição já for falsa a
conjunção já será falsa.
(D) Hugo é policial e Fernando não é vereador.
? e V, para esta conjunção ser V, Hugo é policial deveria ser V, mas não podemos afirmar nada sobre
ele, portanto não podemos concluir.
(E) Hugo é policial ou Fernando é vereador.
? ou F, como temos uma disjunção simples, pelo menos uma das proposições precisa ser verdadeira,
logo neste caso Hugo é policial deveria ser verdadeiro, mas não podemos afirmar nada sobre ele,
portanto, não podemos concluir a veracidade desta afirmação.
IMPLICAÇÃO LÓGICA
Se uma proposição P (p,q,r,...) implica logicamente ou apenas implica uma proposição Q (p,q,r,...) se
Q (p,q,r,...) é verdadeira (V) todas as vezes que P (p,q,r,...) é verdadeira (V), ou seja, a proposição P
implica a proposição Q, quando a condicional P → Q for uma tautologia.
Representamos a implicação com o símbolo “⇒”, simbolicamente temos:
P (p,q,r,...) ⇒ Q (p,q,r,...).
A não ocorrência de VF na tabela verdade de P → Q, ou ainda que o valor lógico da condicional P →
Q será sempre V, ou então que P → Q é uma tautologia.
Observação: Os símbolos “→” e “⇒” são completamente distintos. O primeiro (“→”) representa a
condicional, que é um conectivo. O segundo (“⇒”) representa a relação de implicação lógica que pode ou
não existir entre duas proposições.

101
Exemplo
A tabela verdade da condicional (p ^ q) → (p ↔ q) será:
p q p ^ q p ↔
q
(p ^ q) → (p
↔ q)
V V V V V
V F F F V
F V F F V
F F F V V
Portanto, (p ^ q) → (p ↔ q) é uma tautologia, por isso (p ^ q) ⇒ (p ↔q).
Em particular:
- Toda proposição implica uma Tautologia: p ⇒ p v ~p
p p v ~p
V V
F V
- Somente uma contradição implica uma contradição: p ^ ~p ⇒ p v ~p → p ^ ~p
p ~p p ^ ~p p v ~p → p ^ ~p
V F F F
F V F F
Propriedades da Implicação Lógica
A implicação lógica goza das propriedades reflexiva e transitiva:
Reflexiva: P (p,q,r,...) ⇒ P (p,q,r,...)
Uma proposição complexa implica ela mesma
Transitiva: Se P (p,q,r,...) ⇒ Q (p,q,r,...) e
Q (p,q,r,...) ⇒ R (p,q,r,...), então
P (p,q,r,...) ⇒ R (p,q,r,...)
Se P ⇒ Q e Q ⇒ R, então P ⇒ R
Exemplificação e Regras de Inferência
Inferência é o ato de derivar conclusões lógicas de proposições conhecidas ou decididamente
verdadeiras. Em outras palavras: é a obtenção de novas proposições a partir de proposições verdadeiras
já existentes. Vejamos as regras de inferência obtidas da implicação lógica:
1 – A tabela verdade das proposições p ^ q, p v q , p ↔ q é:
A proposição “p ^ q” é verdadeira (V) somente na 1ª linha, e também nesta linha as proposições “p v
q” e “p → q” também são. Logo a primeira proposição IMPLICA cada uma das outras duas proposições.
Então:
p ^ q ⇒ p v q
p ^ q ⇒ p → q

102
A tabela acima também demonstram as importantes Regras de Inferência:
Adição – p ⇒ p v q e q ⇒ p v q
Simplificação – p ^ q ⇒ p e p ^ q ⇒ q
2 – A tabela verdade das proposições p ↔ q, p → q e q → p, é:
L p q p ↔ q p → q q → p
1ª V V V V V
2ª V F F F V
3ª F V F V F
4ª F F V V V
A proposição “p ↔ q” é verdadeira (V) na 1ª e 4ª linha e as proposições “p → q” e “q → p” também são
verdadeiras. Logo a primeira proposição IMPLICA cada uma das outras duas proposições. Então:
p ↔ q ⇒ p → q e p ↔ q ⇒ q → p
3 - Dada a proposição: (p v q) ^ ~p sua tabela verdade é:
p q p v q ~p (p v q) ^ ~p
V V V F F
V F V F F
F V V V V
F F F V F
Esta proposição é verdadeira somente na 3ª linha e nesta linha a proposição “q” também verdadeira,
logo subsiste a IMPLICAÇÃO LÓGICA, denominada Regra do Silogismo disjuntivo.
(p v q) ^ ~p ⇒ q
É válido também: (p v q) ^ ~q ⇒ p
4 – A tabela verdade da proposição (p → q) ^ p é:
A proposição é verdadeira somente na 1ª linha, e nesta linha a proposição “q” também é verdadeira,
logo subsiste a IMPLICAÇÃO LÓGICA, também denominada Regra de Modus ponens.
(p → q) ^ p ⇒ q
5 – A tabela verdade das proposições (p → q) ^ ~q e ~p é:

103
A proposição (p → q) ^ ~q é verdadeira somente na 4º linha e nesta a proposição “~p” também é
verdadeira, logo subsiste a IMPLICAÇÃO LÓGICA, denominada de Regra Modus tollens.
(p → q) ^ ~q ⇒ ~p
Observe que “~p” implica “p → q”, isto é: ~p ⇒ p → q
Recapitulando as Regras de Inferência aplicadas a Implicação Lógica:
Adição p ⇒ p v q
q ⇒ p v q
Simplificação p ^ q ⇒ p
p ^ q ⇒ q
Silogismo disjuntivo (p v q) ^ ~p ⇒ q
(p v q) ^ ~q ⇒ p
Modus ponens (p → q) ^ p ⇒ q
Modus tollens (p → q) ^ ~q ⇒ ~p
Referência
ALENCAR FILHO, Edgar de – Iniciação a lógica matemática – São Paulo: Nobel – 2002.
Questões
01. (TJ/PI – Analista Judiciário – Escrivão Judicial – FGV) Renato falou a verdade quando disse:
• Corro ou faço ginástica.
• Acordo cedo ou não corro.
• Como pouco ou não faço ginástica.
Certo dia, Renato comeu muito.
É correto concluir que, nesse dia, Renato:
(A) correu e fez ginástica;
(B) não fez ginástica e não correu;
(C) correu e não acordou cedo;
(D) acordou cedo e correu;
(E) não fez ginástica e não acordou cedo.
02. Dizer que “André é artista ou Bernardo não é engenheiro” é logicamente equivalente a dizer que:
(A) André é artista se e somente Bernardo não é engenheiro.
(B) Se André é artista, então Bernardo não é engenheiro.
(C) Se André não é artista, então Bernardo é engenheiro.
(D) Se Bernardo é engenheiro, então André é artista.
(E) André não é artista e Bernardo é engenheiro.
03. Dizer que “Pedro não é pedreiro ou Paulo é paulista,” é do ponto de vista lógico, o mesmo que
dizer que:
(A) Se Pedro é pedreiro, então Paulo é paulista.
(B) Se Paulo é paulista, então Pedro é pedreiro.
(C) Se Pedro não é pedreiro, então Paulo é paulista.
(D) Se Pedro é pedreiro, então Paulo não é paulista.
(E) Se Pedro não é pedreiro, então Paulo não é paulista.
Respostas
01. Resposta: D.
Na disjunção, para evitarmos que elas fiquem falsas, basta por uma das proposições simples como
verdadeira, logo:
“Renato comeu muito”
Como pouco ou não faço ginástica
F V

104
Corro ou faço ginástica
V F
Acordo cedo ou não corro
V F
Portanto ele:
Comeu muito
Não fez ginástica
Correu, e;
Acordou cedo
02. Resposta D
Na expressão temos ~p v q  p  q  ~q  ~p. Temos duas possibilidades de equivalência p  q:
Se André não é artista , então Bernardo não é engenheiro. Porém não temos essa opção ~q  ~p: Se
Bernardo é engenheiro, então André é artista. Logo reposta letra d).
03. Resposta: A.
Na expressão temos ~p v q  p  q p  q: Se Pedro é pedreiro, então Paulo é paulista. Letra a).
CONJUNTOS
Conjunto13
é uma reunião ou agrupamento, que poderá ser de pessoas, seres, objetos, classes…,
dos quais possuem a mesma característica e nos dá ideia de coleção.
Noções Primitivas
Na teoria dos conjuntos, três noções são aceitas sem definições:
- Conjunto;
- Elemento;
- E a pertinência entre um elemento e um conjunto.
Um cacho de bananas, um cardume de peixes ou uma porção de livros são todos exemplos de
conjuntos pois possuem elementos. Um elemento de um conjunto pode ser uma banana, um peixe ou um
livro.
Convém frisar que um conjunto pode ele mesmo ser elemento de algum outro conjunto.
Em geral indicaremos os conjuntos pelas letras maiúsculas A, B, C, ..., X, e os elementos pelas letras
minúsculas a, b, c, ..., x, y, ..., embora não exista essa obrigatoriedade.
A relação de pertinência que nos dá um relacionamento entre um elemento e um conjunto.
Se x é um elemento de um conjunto A, escreveremos x∈A.
Lê-se: x é elemento de A ou x pertence a A.
Se x não é um elemento de um conjunto A, escreveremos xA.
Lê-se x não é elemento de A ou x não pertence a A.
Como Representar um Conjunto
1) Pela designação de seus elementos
Escrevemos os elementos entre chaves, separando os por vírgula.
Exemplos:
13
GONÇALVES, Antônio R. - Matemática para Cursos de Graduação – Contexto e Aplicações
IEZZI, Gelson - Fundamentos da Matemática Elementar – Vol. 01 – Conjuntos e Funções
5 - Noções de conjuntos.

105
{a, e, i, o, u} indica o conjunto formado pelas vogais
{1, 2, 5,10} indica o conjunto formado pelos divisores naturais de 10.
2) Pela sua característica
Escrevemos o conjunto enunciando uma propriedade ou característica comum de seus elementos.
Assim sendo, o conjunto dos elementos x que possuem a propriedade P é indicado por:
{x, | (tal que) x tem a propriedade P}.
Exemplos:
- {x| x é vogal} é o mesmo que {a, e, i, o, u}.
- {x | x são os divisores naturais de 10} é o mesmo que {1, 2, 5,10}.
3) Pelo diagrama de Venn-Euler
Os elementos do conjunto são colocados dentro de uma figura em forma de elipse, chamada diagrama
de Venn.
Exemplos:
- Conjunto das vogais
- Conjunto dos divisores naturais de 10
Igualdade de Conjuntos
Dois conjuntos A e B são ditos iguais (ou idênticos) se todos os seus elementos são iguais, e
escrevemos A = B. Caso haja algum que não o seja, dizemos que estes conjuntos são distintos e
escrevemos A ≠ B.
Exemplos:
a) A = {3, 5, 7} e B = {x| x é primo e 3 ≤ x ≤ 7}, então A = B.
b) B = {6, 9,10} e C = {10, 6, 9}, então B = C, note que a ordem dos elementos não altera a igualdade
dos conjuntos.
Tipos de Conjuntos
- Conjunto Universo
Reunião de todos os conjuntos que estamos trabalhando.
Exemplo:
Quando falamos de números naturais, temos como Conjunto Universo os números inteiros positivos.

106
- Conjunto Vazio
Conjunto vazio é aquele que não possui elementos. Representa-se por 0
 ou, simplesmente { }.
Exemplo:
A = {x| x é natural e menor que 0}.
- Conjunto Unitário
Conjunto caracterizado por possuir apenas um único elemento.
Exemplos:
- Conjunto dos números naturais compreendidos entre 2 e 4. A = {3}.
- Conjunto dos números inteiros negativos compreendidos entre -5 e -7. B = {- 6}.
- Conjuntos Finitos e Infinitos
Finito: quando podemos enumerar todos os seus elementos.
Exemplo: Conjuntos dos Estados da Região Sudeste, S= {Rio de Janeiro, São Paulo, Espirito Santo,
Minas Gerais}.
Infinito: contrário do finito.
Exemplo: Conjunto dos números inteiros, Z = {..., -2, -1, 0, 1, 2, 3, 4, 5, ...}. A reticências representa o
infinito.
Relação de Pertinência
A pertinência é representada pelo símbolo ∈ (pertence) ou 
com conjunto.
Exemplo:
Seja o conjunto B = {1, 3, 5, 7}
1∈ B, 3 ∈ B, 5 ∈ B
2   B , 9  B
Subconjuntos
Quando todos os elementos de um conjunto A são também elementos de um outro conjunto B, dizemos
que A é subconjunto de B.
Podemos dizer ainda que subconjunto é quando formamos vários conjuntos menores com as mesmas
caraterísticas de um conjunto maior.
Exemplos:
- B = {2, 4} ⊂ A = {2, 3, 4, 5, 6}, pois 2 ∈ {2, 3, 4, 5, 6} e 4 ∈ {2, 3, 4, 5 ,6}
- C = {2, 7, 4}  A = {2, 3, 4, 5, 6}, pois 7  {2, 3, 4, 5, 6}
- D = {2, 3} ⊂ E = {2, 3}, pois 2 ∈ {2, 3} e 3 ∈ {2, 3}

107
DICAS:
1) Todo conjunto A é subconjunto dele próprio;
2) O conjunto vazio, por convenção, é subconjunto de qualquer conjunto;
3) O conjunto das partes é o conjunto formado por todos os subconjuntos de A.
Exemplo: Pegando o conjunto B acima, temos as partes de B:
B= {{ },{2},{4},B}
Podemos concluir com essa propriedade que: Se B tem n elementos, então B possui 2n
subconjuntos e, portanto, P(B) possui 2n
elementos.
Se quiséssemos saber quantos subconjuntos tem o conjunto A = {2, 3, 4, 5, 6}, basta calcularmos
aplicando o fórmula:
Números de elementos(n)= 5 → 2n
= 25
= 32 subconjuntos, incluindo o vazio e ele próprio.
Relação de Inclusão
Deve ser usada para estabelecer a relação entre conjuntos com conjuntos, verificando se um conjunto
é subconjunto ou não de outro conjunto.
Representamos as relações de inclusão pelos seguintes símbolos:
⊂→Está contido ⊃→Contém
⊄→Não está contido ⊅→Não contém
Exemplo:
Seja A = {0, 1, 2, 3, 4, 5} e B = {0, 2, 4}
Dizemos que B ⊂ A ou que A ⊃ B
Operações com Conjuntos
- União de conjuntos
A união (ou reunião) dos conjuntos A e B é o conjunto formado por todos os elementos que pertencem
a A ou a B. Representa-se por A U B.
Simbolicamente: A U B = {x | x∈A ou x∈B}
Exemplos:
- {2, 3} U {4, 5, 6} = {2, 3, 4, 5, 6}
- {2, 3, 4} U {3, 4, 5} = {2, 3, 4, 5}
- {2, 3} U {1, 2, 3, 4} = {1, 2, 3, 4}
- {a, b} U  = {a, b}
- Intersecção de conjuntos
A intersecção dos conjuntos A e B é o conjunto formado por todos os elementos que pertencem,
simultaneamente, a A e a B. Representa-se por A∩B. Simbolicamente: A∩B = {x | x ∈ A e x ∈ B}
Exemplos:
- {2, 3, 4} ∩ {3, 5} = {3}
- {1, 2, 3} ∩{2, 3, 4} = {2, 3}
- {2, 3} ∩{1, 2, 3, 5} = {2, 3}
- {2, 4} ∩{3, 5, 7} = 
Observação: Se A∩B = , dizemos que A e B são conjuntos disjuntos.

108
- Propriedades dos conjuntos disjuntos
1) A U (A ∩ B) = A
2) A ∩ (A U B) = A
3) Distributiva da reunião em relação à intersecção: A U (B U C) = (A U B) ∩ (A U C)
4) Distributiva da intersecção em relação à união: A ∩ (B U C) = (A ∩ B) U (A ∩ C)
- Número de Elementos da União e da Intersecção de Conjuntos
Dados dois conjuntos A e B, como vemos na figura abaixo, podemos estabelecer uma relação entre
os respectivos números de elementos.
𝑛(𝐴 ∪ 𝐵) = 𝑛(𝐴) + 𝑛(𝐵) − 𝑛(𝐴 ∩ 𝐵)
Note que ao subtrairmos os elementos comuns (𝑛(𝐴 ∩ 𝐵)) evitamos que eles sejam contados duas
vezes.
Observações:
a) Se os conjuntos A e B forem disjuntos ou se mesmo um deles estiver contido no outro, ainda assim
a relação dada será verdadeira.
b) Podemos ampliar a relação do número de elementos para três ou mais conjuntos com a mesma
eficiência.
Observe o diagrama e comprove:
𝑛(𝐴 ∪ 𝐵 ∪ 𝐶) = 𝑛(𝐴) + 𝑛(𝐵) + 𝑛(𝐶) − 𝑛(𝐴 ∩ 𝐵) − 𝑛(𝐴 ∩ 𝐶) − 𝑛(𝐵 ∩ 𝐶) + 𝑛(𝐴 ∩ 𝐵 ∩ 𝐶)
- Propriedades da União e Intersecção de Conjuntos
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades:
1) Idempotente: A U A = A e A ∩ A= A
2) Elemento Neutro: A U Ø = A e A ∩ U = A
3) Comutativa: A U B = B U A e A ∩ B = B ∩ A
4) Associativa: A U (B U C) = (A U B) U C e A ∩ (B ∩ C) = (A ∩ B) ∩ C
- Diferença
A diferença entre os conjuntos A e B é o conjunto formado por todos os elementos que pertencem a A
e não pertencem a B. Representa-se por A – B. Para determinar a diferença entre conjuntos, basta
observamos o que o conjunto A tem de diferente de B.
Simbolicamente: A – B = {x | x ∈ A e x  B}

109
Exemplos:
- A = {0, 1, 2, 3} e B = {0, 2}  A – B = {1, 3} e B – A =
- A = {1, 2, 3} e B = {2, 3, 4}  A – B = {1} e B – A = {4}
- A = {0, 2, 4} e B = {1 ,3 ,5}  A – B = {0, 2, 4} e B – A = {1, 3, 5}
Note que A – B ≠ B - A
- Complementar
Dados dois conjuntos A e B, tais que B ⊂ A (B é subconjunto de A), chama-se complementar de B
em relação a A o conjunto A - B, isto é, o conjunto dos elementos de A que não pertencem a B.
Dizemos complementar de B em relação a A.
Exemplos:
Seja S = {0, 1, 2, 3, 4, 5, 6}. Então:
a) A = {2, 3, 4} A
 = {0, 1, 5, 6}
b) B = {3, 4, 5, 6 } B
 = {0, 1, 2}
c) C =  C
 = S
Resolução de Problemas Utilizando Conjuntos
Muitos dos problemas constituem- se de perguntas, tarefas a serem executadas. Nos utilizaremos
dessas informações e dos conhecimentos aprendidos em relação as operações de conjuntos para
resolvê-los.
Exemplos:
1) Numa pesquisa sobre a preferência por dois partidos políticos, A e B, obteve-se os seguintes
resultados. Noventa e duas disseram que gostam do partido A, oitenta pessoas disseram que gostam do
partido B e trinta e cinco pessoas disseram que gostam dos dois partidos. Quantas pessoas responderam
à pesquisa?
Resolução pela Fórmula
» n(A U B) = n(A) + n(B) – n(A ∩ B)
» n(A U B) = 92 + 80 – 35
» n(A U B) = 137
Resolução pelo Diagrama:
- Se 92 pessoas responderam gostar do partido A e 35 delas responderam que gostam de ambos,
então o número de pessoas que gostam somente do partido A é: 92 – 35 = 57.
- Se 80 pessoas responderam gostar do partido B e 35 delas responderam gostar dos dois partidos,
então o número de operários que gostam somente do partido B é: 80 – 35 = 45.
- Se 57 gostam somente do partido A, 45 responderam que gostam somente do partido B e 35
responderam que gostam dos dois partidos políticos, então o número de pessoas que responderam à
pesquisa foi: 57 + 35 + 45 = 137.

110
2) Num grupo de motoristas, há 28 que dirigem automóvel, 12 que dirigem motocicleta e 8 que dirigem
automóveis e motocicleta. Quantos motoristas há no grupo?
(A) 16 motoristas
(B) 32 motoristas
(C) 48 motoristas
(D) 36 motoristas
Resolução:
Os que dirigem automóveis e motocicleta: 8
Os que dirigem apenas automóvel: 28 – 8 = 20
Os que dirigem apenas motocicleta: 12 – 8 = 4
A quantidade de motoristas é o somatório: 20 + 8 + 4 = 32 motoristas.
Resposta: B
3) Em uma cidade existem duas empresas de transporte coletivo, A e B. Exatamente 70% dos
estudantes desta cidade utilizam a Empresa A e 50% a Empresa B. Sabendo que todo estudante da
cidade é usuário de pelo menos uma das empresas, qual o % deles que utilizam as duas empresas?
(A) 20%
(B) 25%
(C) 27%
(D) 33%
(E) 35%
Resolução:
70 – 50 = 20.
20% utilizam as duas empresas.
Resposta: A.
Questões
01. (Câmara de São Paulo/SP – Técnico Administrativo – FCC) Dos 43 vereadores de uma cidade,
13 dele não se inscreveram nas comissões de Educação, Saúde e Saneamento Básico. Sete dos
vereadores se inscreveram nas três comissões citadas. Doze deles se inscreveram apenas nas
comissões de Educação e Saúde e oito deles se inscreveram apenas nas comissões de Saúde e
Saneamento Básico. Nenhum dos vereadores se inscreveu em apenas uma dessas comissões. O número
de vereadores inscritos na comissão de Saneamento Básico é igual a
(A) 15.
(B) 21.
(C) 18.
(D) 27.
(E) 16.

111
02. (UFS/SE - Tecnólogo em Radiologia - AOCP) Em uma pequena cidade, circulam apenas dois
jornais diferentes. O jornal A e o jornal B. Uma pesquisa realizada com os moradores dessa cidade
mostrou que 33% lê o jornal A, 45% lê o jornal B, e 7% leem os jornais A e B. Sendo assim, quantos por
centos não leem nenhum dos dois jornais?
(A) 15%
(B) 25%
(C) 27%
(D) 29%
(E) 35%
03. (TRT 19ª – Técnico Judiciário – FCC) Dos 46 técnicos que estão aptos para arquivar documentos
15 deles também estão aptos para classificar processos e os demais estão aptos para atender ao público.
Há outros 11 técnicos que estão aptos para atender ao público, mas não são capazes de arquivar
documentos. Dentre esses últimos técnicos mencionados, 4 deles também são capazes de classificar
processos. Sabe-se que aqueles que classificam processos são, ao todo, 27 técnicos. Considerando que
todos os técnicos que executam essas três tarefas foram citados anteriormente, eles somam um total de
(A) 58.
(B) 65.
(C) 76.
(D) 53.
(E) 95.
04. (Metrô/SP – Oficial Logística – FCC) O diagrama indica a distribuição de atletas da delegação de
um país nos jogos universitários por medalha conquistada. Sabe-se que esse país conquistou medalhas
apenas em modalidades individuais. Sabe-se ainda que cada atleta da delegação desse país que ganhou
uma ou mais medalhas não ganhou mais de uma medalha do mesmo tipo (ouro, prata, bronze). De acordo
com o diagrama, por exemplo, 2 atletas da delegação desse país ganharam, cada um, apenas uma
medalha de ouro.
A análise adequada do diagrama permite concluir corretamente que o número de medalhas
conquistadas por esse país nessa edição dos jogos universitários foi de
(A) 15.
(B) 29.
(C) 52.
(D) 46.
(E) 40.
05. (Pref. de Camaçari/BA – Téc. Vigilância em Saúde NM – AOCP) Qual é o número de elementos
que formam o conjunto dos múltiplos estritamente positivos do número 3, menores que 31?
(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
06. (Pref. de Camaçari/BA – Téc. Vigilância Em Saúde NM – AOCP) Considere dois conjuntos A e
B, sabendo que 𝐴 ∩ 𝐵 = {3}, 𝐴 ∪ 𝐵 = {0;1; 2; 3; 5} 𝑒 𝐴 − 𝐵 = {1; 2}, assinale a alternativa que apresenta o
conjunto B.
(A) {1;2;3}
(B) {0;3}
(C) {0;1;2;3;5}

112
(D) {3;5}
(E) {0;3;5}
07. (Pref. de Inês – Técnico em Contabilidade – MAGNUS CONCURSOS) Numa biblioteca são lidos
apenas dois livros, K e Z. 80% dos seus frequentadores leem o livro K e 60% o livro Z. Sabendo-se que
todo frequentador é leitor de pelo menos um dos livros, a opção que corresponde ao percentual de
frequentadores que leem ambos, é representado:
(A) 26%
(B) 40%
(C) 34%
(D) 78%
(E) 38%
08. (Metrô/SP – Engenheiro Segurança do Trabalho – FCC) Uma pesquisa, com 200 pessoas,
investigou como eram utilizadas as três linhas: A, B e C do Metrô de uma cidade. Verificou-se que 92
pessoas utilizam a linha A; 94 pessoas utilizam a linha B e 110 pessoas utilizam a linha C. Utilizam as
linhas A e B um total de 38 pessoas, as linhas A e C um total de 42 pessoas e as linhas B e C um total
de 60 pessoas; 26 pessoas que não se utilizam dessas linhas. Desta maneira, conclui-se corretamente
que o número de entrevistados que utilizam as linhas A e B e C é igual a
(A) 50.
(B) 26.
(C) 56.
(D) 10.
(E) 18.
09. (Pref. de Inês – Técnico em Contabilidade – MAGNUS CONCURSOS) Numa recepção, foram
servidos os salgados pastel e casulo. Nessa, estavam presentes 10 pessoas, das quais 5 comeram pastel,
7 comeram casulo e 3 comeram as duas. Quantas pessoas não comeram nenhum dos dois salgados?
(A) 0
(B) 5
(C) 1
(D) 3
(E) 2
10. (Corpo de Bombeiros/MT – Oficial de Bombeiro Militar – UNEMAT) Em uma pesquisa realizada
com alunos de uma universidade pública sobre a utilização de operadoras de celular, constatou-se que
300 alunos utilizam a operadora A, 270 utilizam a operadora B, 150 utilizam as duas operadoras (A e B)
e 80 utilizam outras operadoras distintas de A e B.
Quantas pessoas foram consultadas?
(A) 420
(B) 650
(C) 500
(D) 720
(E) 800
Comentários
01. Resposta: C
De acordo com os dados temos:
7 vereadores se inscreveram nas 3.
APENAS 12 se inscreveram em educação e saúde (o 12 não deve ser tirado de 7 como costuma fazer
nos conjuntos, pois ele já desconsidera os que se inscreveram nos três)
APENAS 8 se inscreveram em saúde e saneamento básico.
São 30 vereadores que se inscreveram nessas 3 comissões, pois 13 dos 43 não se inscreveram.
Portanto, 30 – 7 – 12 – 8 = 3
Se inscreveram em educação e saneamento 3 vereadores.

113
Em saneamento se inscreveram: 3 + 7 + 8 = 18
02. Resposta: D
26 + 7 + 38 + x = 100
x = 100 - 71
x = 29%
03. Resposta: B
Técnicos arquivam e classificam: 15
Arquivam e atendem: 46 – 15 = 31
Classificam e atendem: 4
Classificam: 15 + 4 = 19 como são 27 faltam 8
Dos 11 técnicos aptos a atender ao público 4 são capazes de classificar processos, logo apenas 11 -
4 = 7 técnicos são aptos a atender ao público.
Somando todos os valores obtidos no diagrama teremos: 31 + 15 + 7 + 4 + 8 = 65 técnicos.
04. Resposta: D
O diagrama mostra o número de atletas que ganharam medalhas.
No caso das intersecções, devemos multiplicar por 2 por ser 2 medalhas e na intersecção das três
medalhas multiplica-se por 3.
Intersecções:
6 ∙ 2 = 12
1 ∙ 2 = 2
4 ∙ 2 = 8
3 ∙ 3 = 9
Somando as outras:
2 + 5 + 8 + 12 + 2 + 8 + 9 = 46
05. Resposta: B
Se nos basearmos na tabuada do 3, teremos o seguinte conjunto
A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
10 elementos.

114
06. Resposta: E
A intersecção dos dois conjuntos, mostra que 3 é elemento de B.
A – B são os elementos que tem em A e não em B.
Então de A  B, tiramos que B = {0; 3; 5}.
07. Resposta: B
80 – x + x + 60 – x = 100
- x = 100 - 140
x = 40%
08. Resposta: E
92-[38-x+x+42-x]+94-[38-x+x+60-x]+110-[42-x+x+60-x]+(38-x)+x+(42-x)+(60-x)+26=200
92 - [80 - x] + 94 - [98 - x] + 110 - [102 - x] + 38 + 42 – x + 60 – x + 26 = 200
92 – 80 +x + 94 – 98 +x + 110 – 102 + x + 166 -2x = 200
x + 462 – 280 = 200  x + 182 = 200  x = 200-182  x = 18
09. Resposta: C
2 + 3 + 4 + x = 10
x = 10 - 9
x = 1
10. Resposta: C

115
300 – 150 = 150
270 – 150 = 120
Assim: 150 + 120 + 150 + 80 = 500(total).
RELAÇÃO
Plano Cartesiano Ortogonal de Coordenadas
Foi criado por René Descartes, ao qual consiste em dois eixos perpendiculares:
1 - Horizontal denominado eixo das abscissas; e
2 - Vertical denominado eixo das ordenadas.
Tem como objetivo localizarmos pontos determinados em um espaço. Além do mais, o plano
cartesiano foi dividido em quadrantes aos quais apresentam as seguintes propriedades em relação ao
par ordenado (x, y) ou (a, b).
Par Ordenado
Quando representamos o conjunto (a, b) ou (b, a) estamos, na verdade, representando o mesmo
conjunto, sem nos preocuparmos com a ordem dos elementos. Porém, em alguns casos, é conveniente
distinguir a ordem destes elementos.
Para isso, usamos a ideia de par ordenado que é conjunto formado por dois elementos, onde o
primeiro é a ou x e o segundo é b ou y.
Exemplos:
1) (a,b) = (2,5) → a = 2 e b = 5.
2) (a + 1,6) = (5,2b) → a + 1 = 5 e 6 = 2b → a = 5 -1 e b = 6/2 → a = 4 e b = 3.
6 - Relações e funções; Funções polinomiais; Funções exponenciais e
logarítmicas.

116
Gráfico Cartesiano do Par Ordenado
Todo par ordenado de números reais pode ser representado por um ponto no plano cartesiano.
Temos que:
- P é o ponto de coordenadas a e b;
- o número a é chamado de abscissa de P;
- o número b é chamado ordenada de P;
- a origem do sistema é o ponto O (0,0).
Vejamos a representação dos pontos abaixo:
A (4,3)
B (1,2)
C (-2,4)
D (-3,-4)
E (3,-3)
F (-4,0)
G (0,-2)
Produto Cartesiano
Dados dois conjuntos A e B, chamamos de produto cartesiano A x B ao conjunto de todos os possíveis
pares ordenados, de tal maneira que o 1º elemento pertença ao 1º conjunto (A) e o 2º elemento pertença
ao 2º conjunto (B).
𝐀 𝐱 𝐁 = {(𝐱, 𝐲)|𝐱 ∈ 𝐀 𝐞 𝐲 ∈ 𝐁}
Quando o produto cartesiano for efetuado entre o conjunto A e o conjunto A, podemos representar A
x A = A2
. Vejamos, por meio de o exemplo a seguir, as formas de apresentação do produto cartesiano.
Exemplo
Sejam A = {2,3,4} e B = {3,5}. Podemos efetuar o produto cartesiano A x B, também chamado A
cartesiano B, e apresentá-lo de várias formas.
Listagem dos Elementos
Apresentamos o produto cartesiano por meio da listagem, quando escrevemos todos os pares
ordenados que constituam o conjunto. Assim, no exemplo dado, teremos:
A x B = {(2,3),(2,5),(3,3),(3,5),(4,3),(4,5)}
Vamos aproveitar os mesmo conjuntos A e B e efetuar o produto B e A (B cartesiano A):
B x A = {(3,2),(3,3),(3,4),(5,2),(5,3),(5,4)}.
Observando A x B e B x A, podemos notar que o produto cartesiano não tem o privilégio da propriedade
comutativa, ou seja, A x B é diferente de B x A. Só teremos a igualdade A x B = B x A quando A e B forem
conjuntos iguais.

117
Observação: Considerando que para cada elemento do conjunto A o número de pares ordenados
obtidos é igual ao número de elementos do conjunto B, teremos: n (A x B) = n(A) . n(B).
No nosso exemplo temos: n (A x B) = n (A) . n (B) = 3 . 2 = 6
Diagrama de Flechas
Apresentamos o produto cartesiano por meio do diagrama de flechas, quando representamos cada um
dos conjuntos no diagrama de Euler-Venn, e os pares ordenados por “flechas” que partem do 1º elemento
do par ordenado (no 1º conjunto) e chegam ao 2º elemento do par ordenado (no 2º conjunto).
Considerando os conjuntos A e B do nosso exemplo, o produto cartesiano A x B fica assim
representado no diagrama de flechas:
Plano Cartesiano
Apresentamos o produto cartesiano, no plano cartesiano, quando representamos o 1º conjunto num
eixo horizontal, e o 2º conjunto num eixo vertical de mesma origem e, por meio de pontos, marcamos os
elementos desses conjuntos. Em cada um dos pontos que representam os elementos passamos retas
(horizontais ou verticais). Nos cruzamentos dessas retas, teremos pontos que estarão representando, no
plano cartesiano, cada um dos pares ordenados do conjunto A cartesiano B (B x A).
Noção de Relação
Dado os conjuntos A = {4,5,6} e B = {5,6,7,8}, temos:
A x B = {(4,5), (4,6), (4,7), (4,8), (5,5), (5,6), (5,7), (5,8), (6,5), (6,6), (6,7), (6,8)}
Destacando o conjunto A x B, por exemplo, o conjunto R formado pelos pares (x,y) que satisfaçam a
seguinte lei de formação: x + y = 10, ou seja:
R = {(x,y) ϵ A x B| x + y = 10}
Vamos montar uma tabela para facilitar os cálculos.
Destacamos os pares que satisfazem a lei de formação:
R = {(4,6), (5,5)}, podemos com isso observar que R ⊂ A x B.
Dados dois conjuntos A e B, chama-se relação de A em B qualquer subconjunto de A x B, isto é:
R é uma relação de A em B ↔ R ⊂ A x B
Noção de Função
Dados os conjuntos A = {4,5,6} e B = {5,6,7,8}, considerando o conjunto de pares (x,y), tais que x ϵ A
e y ϵ B.
Qualquer um desses conjuntos é chamado relação de A em B, mas se cada elemento dessa relação
associar cada elemento de A um único elemento de B, dizemos que ela é uma função de A em B.
Vale ressaltar que toda função é uma relação, mas nem toda relação é uma função.

118
Analisemos através dos diagramas de Venn.

119
Analisemos agora através dos gráficos:
Um jeito prático de descobrirmos se o gráfico apresentado é ou não função, é traçarmos retas
paralelas ao eixo do y e se verificarmos se no eixo do x existem elementos com mais de uma
correspondência, aí podemos dizer se é ou não uma função, conforme os exemplos acima.
Elementos da Função
Como já vimos nos conceitos acima, temos que, dado dois conjuntos não vazios A e B chamamos de
função a relação que associa a cada elemento de x (ou a) de A um único elemento y (ou b) de B,
conhecida também como função de A em B.
Na figura abaixo está ilustrado os elementos de uma função.
Pelo diagrama de Venn:
Representado no gráfico:
- Ao conjunto A dá-se o nome de domínio, ou conjunto partida, representado pela letra D.
Logo, D(f) = A.

120
- Ao conjunto B dá-se o nome de contradomínio, ou conjunto chegada, representado pelas letras CD
ou somente C. Logo, CD(f) = B ou C(f) = B.
- A cada elemento y de B que está associado a um x de A, denominamos imagem de x. Logo, y = f(x).
(Lê-se: y é igual a f de x).
- Ao conjunto dos elementos y de B, que são imagens dos elementos x de A, dá-se o nome de conjunto
imagem ou apenas imagem, representado por Im ou Im(f). Têm:-se que Im ⊂ B.
A notação para representar função é dada por:
Exemplo
Dado A = {-2, -1, 0, 1, 2} vamos determinar o conjunto imagem da função f:A→ R, definida por f(x) =
x+3.
Vamos pegar cada elemento do conjunto A, aplicarmos a lei de associação e acharmos a imagem
deste conjunto.
F(-2) = -2 + 3 = 1
F(-1) = -1 + 3 = 2
F(0) = 0 + 3 = 3
F(1) = 1 + 3 = 4
F(2) = 2 + 3 = 5
Domínio de uma Função Real de Variável Real
Para definirmos uma função precisamos conhecer dois conjuntos (não vazios) A e B e a lei que associa
cada elemento x de A um único elemento y de B. Para nosso caso vamos considerar A e B sendo
subconjuntos de R e diremos que f é uma função real de variável real.
O conjunto A, domínio da função f, será formado por todos os elementos do conjunto real de x, para
os quais as operações indicadas na lei de associação sejam possíveis em R.
Exemplos
1) y = x2
+ 3x
Vamos substituir x por qualquer número real e obtermos para y um valor real. Logo D(f) = R.
2) 𝑦 =
1
𝑥
Neste caso como o nosso denominador não pode ser igual a zero, temos que D(f) = R*
3) 𝒇(𝒙) =
𝒙
𝒙−𝟐
Como sabemos que o denominador tem que ser diferente de zero, logo x – 2 ≠ 0  x ≠ 2.
D(f) = R – {2} ou D(f) = {x ϵ R| x ≠ 2}
Questão
01. Dado o conjunto A= {0, 1, 2, 3, 4}, e seja a função f: A→ R, da função f(x) = 2x + 3. O conjunto
imagem desta função será?
(A) Im = {3, 5, 7, 9, 11}
(B) Im = {0, 1, 2, 3, 4}
(C) Im = {0, 5, 7, 9, 11}
(D) Im = {5, 7, 9,11}
(E) Im = {3, 4, 5, 6, 7}

121
Comentário
01. Resposta: A
Basta substituirmos o x da função f(x) = 2x + 3 pelos elementos de A.
Então:
f(0) = 2.0 + 3 = 0 + 3 = 3
f(1) = 2.1 + 3 = 2 + 3 = 5
f(2) = 2.2 + 3 = 4 + 3 = 7
f(3) = 2.3 + 3 = 6 + 3 = 9
f(4) = 2.4 + 3 = 8 + 3 = 11
Assim Im = {3, 5, 7, 9, 11}
FUNÇÃO DO 1º GRAU OU FUNÇÃO AFIM OU POLINOMIAL DO 1º GRAU
Função do 1º grau ou função afim ou polinomial do 1º grau recebe ou é conhecida por um desses
nomes, sendo por definição14
: Toda função f: R → R, definida por:
Com a ϵ R* e b ϵ R.
O domínio e o contradomínio é o conjunto dos números reais (R) e o conjunto imagem coincide com o
contradomínio, Im = R.
Quando b = 0, chamamos de função linear.
Gráfico de uma Função
Dada a função y = 2x + 3 (a = 2 > 0). Vamos montar o gráfico dessa função.
Para montarmos o gráfico vamos atribuir valores a x para acharmos y.
x y (x,y)
0 y = 2 .0 + 3 = 3 (0,3)
-2 y = 2 . (-2) + 3 = - 4 + 3 = -1 (-2,-1)
-1 y = 2 .(-1) + 3 = -2 + 3 = 1 (-1,1)
Construção do gráfico no plano cartesiano:
Observe que a reta de uma função afim é
sempre uma reta.
E como a > 0 ela é função crescente, que
veremos mais à frente
Vejamos outro exemplo: f(x) = –x + 1. Montando o gráfico temos:
14
BIANCHINI, Edwaldo; PACCOLA, Herval – Matemática Volume 1 – Editora Moderna
FACCHINI, Walter – Matemática Volume Único – 1ª Edição - Editora Saraiva:1996

122
Observe que a < 0, logo é uma função decrescente
Tipos de Função
Função constante: é toda função definida f: R → R, para cada elemento de x, temos a mesma
imagem, ou seja, o mesmo f(x) = y. Podemos dizer que y = f(x) = k.
Observe os gráficos abaixo da função constante
A representação gráfica de uma função do constante, é uma reta paralela ao eixo das abscissas ou
sobre o eixo (igual ao eixo das abscissas).
Função Identidade
Se a = 1 e b = 0, então y = x. Quando temos este caso chamamos a função de identidade, notamos
que os valores de x e y são iguais, quando a reta corta os quadrantes ímpares e y = - x, quando corta
os quadrantes pares.
A reta que representa a função identidade é denominada de bissetriz dos quadrantes ímpares:
E no caso abaixo a reta é a bissetriz dos quadrantes pares.
Função Injetora
Quando para n elementos distintos do domínio apresentam imagens também distintas no
contradomínio.

123
Reconhecemos, graficamente, uma função injetora quando, uma reta horizontal, qualquer que seja
interceptar o gráfico da função, uma única vez.
Se traçarmos retas horizontais, paralelas ao
eixo x, notaremos que o mesmo cortará a reta
formada pela função em um único ponto (o que
representa uma imagem distinta), logo
concluímos que se trata de uma função injetora.
Função Sobrejetora
Quando todos os elementos do contradomínio forem imagens de pelo menos um elemento do domínio.
Reconhecemos, graficamente, uma função sobrejetora quando, qualquer que seja a reta horizontal
que interceptar o eixo no contradomínio, interceptar, também, pelo menos uma vez o gráfico da função.
Observe que todos os elementos do
contradomínio tem um correspondente em x.
Logo é sobrejetora.
Im(f) = B

124
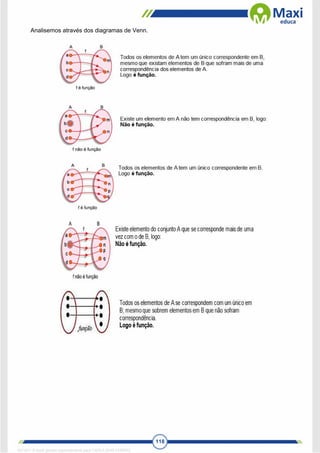
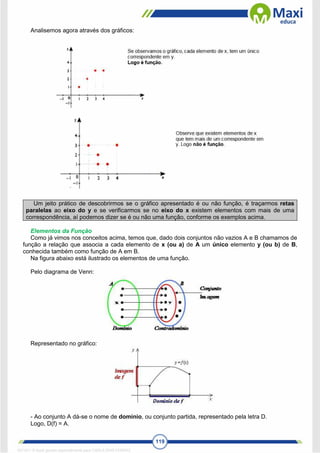
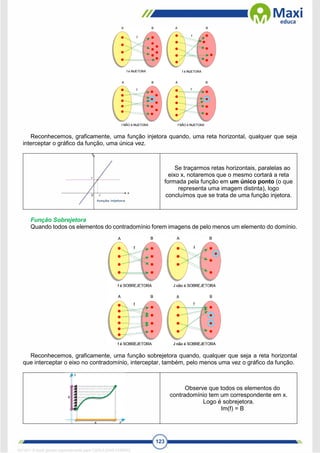
Observe que nem todos os elementos do
contradomínio tem um correspondente em x.
Logo não é sobrejetora.
Im(f) ≠ B
Função Bijetora
uma função é dita bijetora quando é injetora e sobrejetora ao mesmo tempo.
Exemplo:
A função f : [1; 3] → [3; 5], definida por f(x) = x + 2, é uma função bijetora.
Função Ímpar e Função Par
Dizemos que uma função é par quando para todo elemento x pertencente ao domínio temos 𝑓(𝑥) =
𝑓(−𝑥), ∀ 𝑥 ∈ 𝐷(𝑓). Ou seja os valores simétricos devem possuir a mesma imagem. Par melhor
compreensão observe o diagrama abaixo:
A função é dita ímpar quando para todo elemento x pertencente ao domínio, temos f(-x) = -f(x) ∀ x є
D(f). Ou seja os elementos simétricos do domínio terão imagens simétricas. Observe o diagrama abaixo:

125
Função crescente e decrescente
A função pode ser classificada de acordo com o valor do coeficiente a (coeficiente angular da reta),
se a > 0, a função é crescente, caso a < 0, a função é decrescente. A função é caracterizada por uma
reta.
Observe que medida que os valores de x
aumentam, os valores de y ou f(x) também
aumentam.
Observe que medida que os valores de x
aumentam, os valores de y ou f(x) diminuem.
Através do gráfico da função notamos que:
- Para função é crescente o ângulo formado entre a reta da função e o eixo x (horizontal) é agudo
(< 90º) e
- Para função decrescente o ângulo formado é obtuso (> 90º).
Zero ou Raiz da Função
Chama-se zero ou raiz da função y = ax + b, o valor de x que anula a função, isto é, o valor de x para
que y ou f(x) seja igual à zero.
Para achar o zero da função y = ax + b, basta igualarmos y ou f(x) a valor de zero, então assim teremos
uma equação do 1º grau, ax + b = 0.
Exemplo:
Determinar o zero da função:
f(x) = x + 3
Igualamos f(x) = 0 → 0 = x + 3 → x = -3
Graficamente temos:
No plano cartesiano, o zero da função é representado pela abscissa do ponto onde a reta corta o eixo
x.
Observe que a reta f(x) = x+3 intercepta o eixo x no ponto (-3,0), ou seja, no ponto de abscissa -3,
que é o zero da função. Observamos que como a > 0, temos que a função é crescente.

126
Partindo equação ax + b = 0 podemos também escrever de forma simplificada uma outra maneira de
acharmos a raiz da função utilizando apenas os valores de a e b.
𝒂𝒙 + 𝒃 = 𝟎 → 𝒂𝒙 = −𝒃 → 𝒙 =
−𝒃
𝒂
Podemos expressar a fórmula acima graficamente:
Estudo do sinal da Função
Estudar o sinal da função y = ax + b é determinar os valores reais de x para que:
- A função se anule (y = 0);
- A função seja positiva (y > 0);
- A função seja negativa (y < 0).
Vejamos abaixo o estudo do sinal:
Exemplo:
Estudar o sinal da função y = 2x – 4 (a = 2 > 0).
1) Qual o valor de x que anula a função?
y = 0
2x – 4 = 0
2x = 4
x =
2
4
x = 2
A função se anula para x = 2.

127
2) Quais valores de x tornam positiva a função?
y > 0
2x – 4 > 0
2x > 4
x >
2
4
x > 2
A função é positiva para todo x real maior que 2.
3) Quais valores de x tornam negativa a função?
y < 0
2x – 4 < 0
2x < 4
x <
2
4
x < 2
A função é negativa para todo x real menor que 2.
Podemos também estudar o sinal da função por meio de seu gráfico:
- Para x = 2 temos y = 0;
- Para x > 2 temos y > 0;
- Para x < 2 temos y < 0.
Questões
01. (MPE/SP - Geógrafo - VUNESP) O gráfico apresenta informações do lucro, em reais, sobre a
venda de uma quantidade, em centenas, de um produto em um hipermercado.
Sabendo-se que é constante a razão entre a variação do lucro e a variação da quantidade vendida e
que se pretende ter um lucro total não menor que R$ 90.500,00 em 10 dias de venda desse produto,
então a média diária de unidades que deverão ser vendidas, nesse período, deverá ser, no mínimo, de:
(A) 8 900.
(B) 8 950.
(C) 9 000.
(D) 9 050.
(E) 9 150.

128
02. (Pref. Jundiaí/SP - Eletricista - MAKIYAMA) Em determinado estacionamento cobra-se R$ 3,00
por hora que o veículo permanece estacionado. Além disso, uma taxa fixa de R$ 2,50 é somada à tarifa
final. Seja t o número de horas que um veículo permanece estacionado e T a tarifa final, assinale a seguir
a equação que descreve, em reais, o valor de T:
(A) T = 3t
(B) T = 3t + 2,50
(C) T = 3t + 2.50t
(D) T = 3t + 7,50
(E) T = 7,50t + 3
03. (PM/SP - Sargento CFS - CETRO) Dada a função f(x) = −4x +15 , sabendo que f(x) = 35, então
(A) x = 5.
(B) x = 6.
(C) x = -6.
(D) x = -5.
04. (BNDES - Técnico Administrativo - CESGRANRIO) O gráfico abaixo apresenta o consumo médio
de oxigênio, em função do tempo, de um atleta de 70 kg ao praticar natação.
Considere que o consumo médio de oxigênio seja diretamente proporcional à massa do atleta.
Qual será, em litros, o consumo médio de oxigênio de um atleta de 80 kg, durante 10 minutos de prática
de natação?
(A) 50,0
(B) 52,5
(C) 55,0
(D) 57,5
(E) 60,0
05. (PETROBRAS - Técnico Ambiental Júnior - CESGRANRIO)
de domínio real, então, m − p é igual a
(A) 3
(B) 4
(C) 5
(D) 64
(E) 7
06. (CBTU/RJ - Assistente Operacional - CONSULPLAN) A função inversa de uma função f(x) do 1º
grau passa pelos pontos (2, 5) e (3, 0). A raiz de f(x) é
(A) 2.
(B) 9.
(C) 12.
(D) 15.

129
07. (BRDE/RS - Técnico Administrativo) Numa firma, o custo para produzir x unidades de um produto
é C(x) =
𝑥
2
+ 10000, e o faturamento obtido com a comercialização dessas x unidades é f(x) =
2
3
𝑥. Para
que a firma não tenha prejuízo, o faturamento mínimo com a comercialização do produto deverá ser de:
(A) R$ 20.000,00
(B) R$ 33.000,00
(C) R$ 35.000,00
(D) R$ 38.000,00
(E) R$ 40.000,00
08. (CBTU/RJ - Assistente Operacional - CONSULPLAN) Qual dos pares de pontos a seguir
pertencem a uma função do 1º grau decrescente?
(A) Q(3, 3) e R(5, 5).
(B) N(0, –2) e P(2, 0).
(C) S(–1, 1) e T(1, –1).
(D) L(–2, –3) e M(2, 3).
09. (CBTU/RJ - Assistente Operacional - CONSULPLAN) A reta que representa a função f(x) = ax +
b intercepta o eixo y no ponto (0, 4) e passa pelo ponto (–1, 3). A raiz dessa função é
(A) –4.
(B) –2.
(C) 1.
(D) 2.
10. (Corpo de Bombeiros Militar/MT - Oficial Bombeiro Militar - UNEMAT) O planeta Terra já foi
um planeta incandescente segundo estudos e está se resfriando com o passar dos anos, mas seu núcleo
ainda está incandescente.
Em certa região da terra onde se encontra uma mina de carvão mineral, foi constatado que, a cada 80
metros da superfície, a temperatura no interior da Terra aumenta 2 graus Celsius.
Se a temperatura ambiente na região da mina é de 23° Celsius, qual a temperatura no interior da mina
num ponto a 1200 metros da superfície?
(A) 15º C
(B) 38º C
(C) 53º C
(D) 30º C
(E) 61º C
Comentários
01. Resposta: E
Pelo enunciado temos que, a razão constante entre variação de lucro (ΔL) e variação de quantidade
(ΔQ) vendida:
𝑅 =
∆𝐿
∆𝑄
→ 𝑅 =
7000 − (−1000)
80 − 0
→ 𝑅 =
8000
80
→ 𝑅 = 100
Como se pretende ter um lucro maior ou igual a R$ 90.500,00, logo o lucro final tem que ser pelo
menos 90.500,00
Então fazendo a variação do lucro para este valor temos:
ΔL = 90500 – (-1000) = 90500 + 1000 = 91500
Como é constante a razão entre a variação de lucro (ΔL) e variação de quantidade (ΔQ) vendida,
vamos usar o valor encontrado para acharmos a quantidade de peças que precisam ser produzidas:
𝑅 =
∆𝐿
∆𝑄
→ 100 =
91500
∆𝑄
→ 100∆𝑄 = 91500 → ∆𝑄 =
91500
100
→ ∆𝑄 = 915
Como são em 10 dias, termos 915 x 10 = 9150 peças que deverão ser vendidas, em 10 dias, para que
se obtenha como lucro pelo menos um lucro total não menor que R$ 90.500,00

130
02. Resposta: B
Equacionando as informações temos: 3 deve ser multiplicado por t, pois depende da quantidade de
tempo, e acrescentado 2,50 fixo
T = 3t + 2,50
03. Resposta: D
35 = - 4x + 15 → - 4x = 20 → x = - 5
04. Resposta: E
A proporção de oxigênio/tempo:
10,5
2
=
21,0
4
=
𝑥
10
4x = 210
x = 52,5 litros de oxigênio em 10 minutos para uma pessoa de 70 kg
52,5litros----70kg
x-------------80kg
x = 60 litros
05. Resposta: C
Aplicando segundo as condições mencionadas:
x = 1
f(1) = 2.1 - p
f(1) = m - 1
x = 6
f(6) = 6m - 1
𝑓(6) =
7.6+4
2
=
42+4
2
= 23 ; igualando as duas equações:
23 = 6m - 1
m = 4
Como queremos m – p , temos:
2 - p = m - 1 ; igualando as duas novamente.
2 – p = 4 – 1 → p = - 1 → m – p = 4 - (- 1) = 5
06. Resposta: D
Primeiramente, vamos calcular os valores de a e b:
Sabendo que f(x) = y , temos que y = ax + b.
* a: basta substituir os pontos T (2, 5) e V (3, 0) na equação. Assim:
( T ) 5 = a.2 + b , ou seja, 2.a + b = 5 ( I )
( V ) 0 = a.3 + b , ou seja, 3.a + b = 0 , que fica b = – 3.a ( II )
Substituindo a equação ( II ) na equação ( I ), temos:
2.a + (– 3.a) = 5 → 2.a – 3.a = 5 → – a = 5 . (– 1) → a = – 5
Para calcular o valor de b, vamos substituir os valores de um dos pontos e o valor de a na equação.
Vamos pegar o ponto V (3, 0) para facilitar os cálculos:
y = a.x + b
0 = – 5.3 + b
b = 15
Portanto, a função fica: y = – 5.x + 15 .
Agora, precisamos calcular a função inversa: basta trocar x por y e vice-versa. Assim:
x = – 5.y + 15
5.y = – x +15
y = – x / 5 + 15/5
y = – x / 5 + 3 (função inversa)
Por fim, a raiz é calculada fazendo y = 0. Assim:
0 = – x / 5 + 3 → x / 5 = 3 → x = 3 . 5 → x = 15

131
07. Resposta: E
C(x) =
𝑥
2
+ 10000
F(x) =
2
3
𝑥
F(x) ≥ C(x)
2
3
𝑥 ≥
𝑥
2
+ 10000
2
3
𝑥 −
𝑥
2
≥ 10000 
4𝑥−3𝑥
6
≥ 10000 
4𝑥−3𝑥
6
≥ 10000 x =
10000
1
6
 x ≥ 60000, como ele quer o menor
valor.
Substituindo no faturamento as 60000 unidades temos:
F(x) =
2
3
60000 = 40.000
Portanto o resultado final é de R$ 40.000,00.
08. Resposta: C
Para pertencer a uma função polinomial do 1º grau decrescente, o primeiro ponto deve estar em uma
posição “mais alta” do que o 2º ponto.
Vamos analisar as alternativas:
( A ) os pontos Q e R estão no 1º quadrante, mas Q está em uma posição mais baixa que o ponto R,
e, assim, a função é crescente.
( B ) o ponto N está no eixo y abaixo do zero, e o ponto P está no eixo x à direita do zero, mas N está
em uma posição mais baixa que o ponto P, e, assim, a função é crescente.
( D ) o ponto L está no 3º quadrante e o ponto M está no 1º quadrante, e L está em uma posição mais
baixa do que o ponto M, sendo, assim, crescente.
( C ) o ponto S está no 2º quadrante e o ponto T está no 4º quadrante, e S está em uma posição mais
alta do que o ponto T, sendo, assim, decrescente.
09. Resposta: A
Primeiramente, vamos calcular os valores de a e b:
Sabendo que f(x) = y , temos que y = ax + b.
* a: basta substituir os pontos T (0, 4) e V (–1, 3) na equação. Assim:
( T ) 4 = a.0 + b , ou seja, b = 4
( V ) 3 = a.( – 1) + b
a = 4 – 3 = 1
Portanto, a função fica: y = x + 4
Por fim, a raiz é calculada fazendo y = 0. Assim:
0 = x + 4 , ou seja, x = – 4
10. Resposta: C
Vamos utilizar a função T(h) = 23 + 2.h, onde T é a temperatura e h é a profundidade. Assim:
A temperatura aumenta: 1200 / 80 = 15 partes
Assim: 15 . 2 = 30º C
Assim: 23º C + 30º C = 53º C
FUNÇÃO DO 2º GRAU
Chama-se função do 2º grau15
, função quadrática, função polinomial do 2º grau ou função trinômio do
2º grau, toda função f de R em R definida por um polinômio do 2º grau da forma:
15
BIANCHINI, Edwaldo; PACCOLA, Herval – Matemática Volume 1 – Editora Moderna
FACCHINI, Walter – Matemática Volume Único – 1ª Edição - Editora Saraiva:1996

132
Com a, b e c reais e a ≠ 0.
Onde:
a é o coeficiente de x2
;
b é o coeficiente de x;
c é o termo independente.
Exemplos
y = x2
– 5x + 6, sendo a = 1, b = – 5 e c = 6
y = x2
– 16, sendo a = 1, b = 0 e c = – 16
f(x) = x2
, sendo a = 1, b = 0 e c = 0
f(x) = 3x2
+ 3x, sendo a = 3 , b = 3 e c = 0
Representação Gráfica da Função
O gráfico da função é constituído de uma curva aberta chamada de parábola.
Vejamos a trajetória de um projétil lançado obliquamente em relação ao solo horizontal, ela é uma
parábola cuja concavidade está voltada para baixo.
Exemplo
Se a função f de R em R definida pela equação y = x2
+ x. Atribuindo à variável x qualquer valor real,
obteremos em correspondência os valores de y, vamos construir o gráfico da função:
1) Como o valor de a > 0 a concavidade está voltada para cima;
2) -1 e 0 são as raízes de f(x);
3) c é o valor onde a curva corta o eixo y, neste caso no 0 (zero);
4) O valor do mínimo pode ser observado nas extremidades (vértice) de cada parábola: -1/2 e -1/4.
Concavidade da Parábola
No caso das funções definida por um polinômio do 2º grau, a parábola pode ter sua concavidade
voltada para cima (a > 0) ou voltada para baixo (a < 0). A concavidade é determinada pelo valor do a
(maior que zero ou menor que zero). Esta é uma característica geral para a função definida por um
polinômio do 2º grau.

133
Vértice da Parábola
Toda parábola tem um ponto de ordenada máxima ou ponto de ordenada mínima, a esse ponto
denominamos vértice. Dado por V (xv , yv).
Eixo de Simetria
É aquele que dado o domínio a imagem é a mesma. Isso faz com que possamos dizer que a parábola
é simétrica a reta que passa por xv, paralela ao eixo y, na qual denominamos eixo de simetria. Vamos
entender melhor o conceito analisando o exemplo: y = x2
+ 2x – 3 (início do assunto).
Atribuímos valores a x, achamos valores para y. Temos que:
f (-3) = f (1) = 0
f (-2) = f (0) = -3
Conjunto Domínio e Imagem
Toda função com Domínio nos Reais (R) que possui a > 0, sua concavidade está voltada para cima, e
o seu conjunto imagem é dado por:
Logo se a < 0, a concavidade estará voltada para baixo, o seu conjunto imagem é dado por:
Coordenadas do Vértice da Parábola
Como visto anteriormente a função apresenta como eixo de simetria uma reta vertical que intercepta
o gráfico num ponto chamado de vértice.
As coordenadas do vértice são dadas por:

134
Onde:
x1 e x2 são as raízes da função.
Valor Máximo e Valor Mínimo
- Se a > 0, o vértice é o ponto da parábola que tem ordenada mínima. Nesse caso, o vértice é chamado
ponto de mínimo e a ordenada do vértice é chamada valor mínimo da função;
- Se a < 0, o vértice é o ponto da parábola que tem ordenada máxima. Nesse caso, o vértice é ponto
de máximo e a ordenada do vértice é chamada valor máximo da função.
Exemplo
Dado a função y = x2
– 2x – 3 vamos construir a tabela e o gráfico desta função, determinando também
o valor máximo ou mínimo da mesma.
Como a = 1 > 0, então a função possui um valor mínimo como pode ser observado pelo gráfico. O
valor de mínimo ocorre para x = 1 e y = - 4. Logo o valor de mínimo é - 4 e a imagem da função é dada
por: Im = { y ϵ R | y ≥ - 4}.
Raízes ou Zeros da Função
As raízes ou zeros da função quadrática f(x) = ax2
+ bx + c são os valores de x reais tais que f(x) = 0,
ou seja são valores que deixam a função nula. Com isso aplicamos o método de resolução da equação
do 2º grau.

135
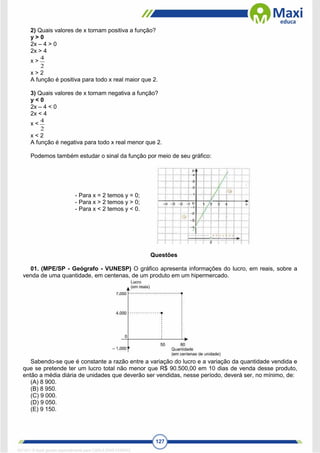
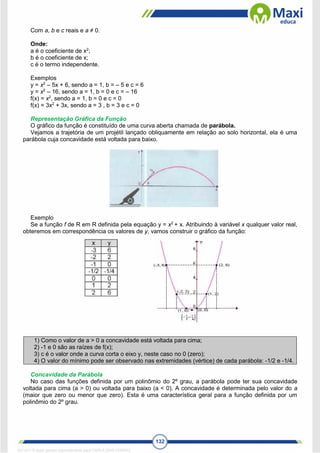
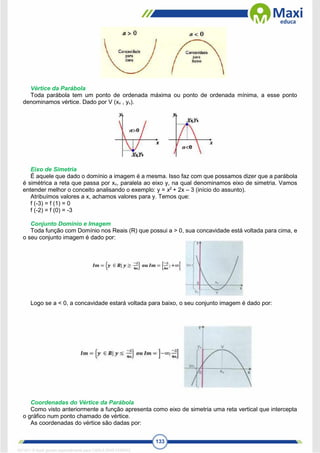
ax2
+ bx + c = 0
A resolução de uma equação do 2º grau é feita com o auxílio da chamada “fórmula de Bháskara”.
a
b
x
.
2



 , onde, = b2
– 4.a.c
As raízes (quando são reais), o vértice e a intersecção com o eixo y são fundamentais para traçarmos
um esboço do gráfico de uma função do 2º grau.
Forma fatorada das raízes: f (x) = a (x – x1) (x – x2).
Esta fórmula é muito útil quando temos as raízes e precisamos montar a sentença matemática que
expresse a função.
Estudo da Variação do Sinal da Função
Estudar o sinal de uma função quadrática é determinar os valores reais de x que tornam a função
positiva, negativa ou nula.
Abaixo podemos resumir todos os valores assumidos pela função dado a e Δ (delta).
Observe que:
Quando Δ > 0, o gráfico corta e tangencia o eixo x em dois pontos distintos, e temos duas raízes
reais distintas.
Quando Δ = 0, o gráfico corta e tangencia o eixo x em um ponto e temos duas raízes iguais.
Quando Δ < 0, o gráfico não corta e não tangencia o eixo x em nenhum ponto e não temos raízes
reais.
Exemplos
1) Considere a função quadrática representada pelo gráfico abaixo, vamos determinar a sentença
matemática que a define.
Resolução:
Como conhecemos as raízes x1 e x2 (x1= - 4 e x2 = 0), podemos utilizar a forma fatorada:
f (x) = a.[ x – (- 4)].[x – 0] ou f (x) = a(x + 4).x .
O vértice da parábola é (- 2,4), temos:
4 = a.(- 2 + 4).(- 2) → a = - 1
Logo, f(x) = - 1.(x + 4).x → (- x - 4x).x → - x2
- 4x
2) Vamos determinar o valor de k para que o gráfico cartesiano de f(x) = -x2
+ (k + 4). x – 5 ,passe pelo
ponto (2;3).

136
Resolução:
Como x = 2 e f(x) = y = 3, temos:
3 = - (2)2
+ (k + 4).2 - 5 → 3 = - 4 + 2k + 8 - 5 → 2k + 8 - 9 = 3 → 2 k - 1 = 3 → 2k = 3 + 1 → 2k = 4 →
k = 2.
Questões
01. (CBM/MG – Oficial Bombeiro Militar – FUMARC) Duas cidades A e B estão separadas por uma
distância d. Considere um ciclista que parte da cidade A em direção à cidade B. A distância d, em
quilômetros, que o ciclista ainda precisa percorrer para chegar ao seu destino em função do tempo t, em
horas, é dada pela função 𝑑(𝑡) =
100−𝑡2
𝑡+1
. Sendo assim, a velocidade média desenvolvida pelo ciclista em
todo o percurso da cidade A até a cidade B é igual a
(A) 10 Km/h
(B) 20 Km/h
(C) 90 Km/h
(D) 100 Km/h
02. (ESPCEX – Cadetes do Exército – Exército Brasileiro) Uma indústria produz mensalmente x
lotes de um produto. O valor mensal resultante da venda deste produto é V(x)=3x²-12x e o custo mensal
da produção é dado por C(x)=5x²-40x-40. Sabendo que o lucro é obtido pela diferença entre o valor
resultante das vendas e o custo da produção, então o número de lotes mensais que essa indústria deve
vender para obter lucro máximo é igual a
(A) 4 lotes.
(B) 5 lotes.
(C) 6 lotes.
(D) 7 lotes.
(E) 8 lotes.
03. (IPEM – Técnico em Metrologia e Qualidade – VUNESP) A figura ilustra um arco decorativo de
parábola AB sobre a porta da entrada de um salão:
Considere um sistema de coordenadas cartesianas com centro em O, de modo que o eixo vertical (y)
passe pelo ponto mais alto do arco (V), e o horizontal (x) passe pelos dois pontos de apoio desse arco
sobre a porta (A e B).
Sabendo-se que a função quadrática que descreve esse arco é f(x) = – x²+ c, e que V = (0; 0,81), pode-
se afirmar que a distância 𝐴𝐵
̅̅̅̅, em metros, é igual a
(A) 2,1.
(B) 1,8.
(C) 1,6.
(D) 1,9.
(E) 1,4.
04. (Polícia Militar/MG – Soldado – Polícia Militar) A interseção entre os gráficos das funções y = -
2x + 3 e y = x² + 5x – 6 se localiza:
(A) no 1º e 2º quadrantes
(B) no 1º quadrante
(C) no 1º e 3º quadrantes
(D) no 2º e 4º quadrantes

137
Comentários
01. Resposta: A
Vamos calcular a distância total, fazendo t = 0:
𝑑(0) =
100−02
0+1
= 100𝑘𝑚
Agora, vamos substituir na função:
0 =
100−𝑡2
𝑡+1
100 – t² = 0
– t² = – 100 . (– 1)
t² = 100
𝑡 = √100 = 10𝑘𝑚/ℎ
02. Resposta: D
L(x) = 3x² - 12x-5x² + 40x + 40
L(x) = - 2x² + 28x + 40
𝑥𝑚á𝑥𝑖𝑚𝑜 = −
𝑏
2𝑎
= −
28
−4
= 7 𝑙𝑜𝑡𝑒𝑠
03. Resposta: B
C = 0,81, pois é exatamente a distância de V
f(x) = - x² + 0,81
0 = - x² + 0,81
x² = 0,81
x =  0,9
A distância AB é 0,9 + 0,9 = 1,8
04. Resposta: A
- 2x + 3 = x² + 5x - 6
x² + 7x - 9 = 0
 = 49 + 36 = 85
𝑥 =
−7 ± √85
2
𝑥1 =
−7 + 9,21
2
= 1,105
𝑥2 =
−7 − 9,21
2
= −8,105
Para x=1,105
y = - 2 . 1,105 + 3 = 0,79
Para x = - 8,105
y = 19,21
Então a interseção ocorre no 1º e no 2º quadrante.
FUNÇÃO EXPONENCIAL
Definição
A função exponencial é a definida como sendo a inversa da função logarítmica natural, isto é:
Podemos concluir, que a função exponencial é definida por:

138
Gráficos da Função Exponencial
Propriedades da Função Exponencial
Se a, x e y são números reais quaisquer e k é um número racional, então:
- ax
. ay
= ax + y
- ax
/ ay
= ax - y
- (ax
) y
= ax.y
- (a b)x
= ax
bx
- (a / b)x
= ax
/ bx
- a-x
= 1 / ax
Estas relações também são válidas para exponenciais de base e (e = número de Euller = 2,718...)
- y = ex
se, e somente se, x = ln(y)
- ln(ex
) = x
- ex+y
= ex
.ey
- ex-y
= ex
/ey
- ex.k
= (ex
)k
Constante de Euler
Existe uma importantíssima constante matemática definida por
e = exp(1)
O número e é um número irracional e positivo, de acordo com a definição da função exponencial, temos
que:
ln(e) = 1
Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler, um dos primeiros
a estudar as propriedades desse número.
O valor deste número expresso com 40 dígitos decimais, é:
e = 2,718281828459045235360287471352662497757
Porém ninguém é obrigado a decorar este número, sabendo com duas casas após a vírgula já é mais
que suficiente, ou seja, devemos saber que e = 2,72 aproximadamente.
Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com
expoente x, isto é:
ex
= exp(x)

139
Construção do Gráfico de uma Função Exponencial
Exemplo:
Vamos construir o gráfico da função 𝑦 = 2𝑥
Vamos atribuir valores a x, para que possamos traçar os pontos no gráfico.
X Y
-3 1
8
-2 1
4
-1 1
2
0 1
1 2
2 4
3 8
Questões
01. (UFOP – Assistente em Administração – UFOP/2018) Sobre a função f(x) = (1/3)-x
, assinale a
afirmativa correta.
(A)f é crescente.
(B) f não é injetora.
(C) O domínio de f é o conjunto dos números reais negativos.
(D) A imagem de f é o conjunto dos números reais.
02. (Corpo de Bombeiros Militar/MT – Oficial Bombeiro Militar – COVEST) As funções
exponenciais são muito usadas para modelar o crescimento ou o decaimento populacional de uma
determinada região em um determinado período de tempo. A função 𝑃(𝑡) = 234 . (1,023)𝑡
modela o
comportamento de uma determinada cidade quanto ao seu crescimento populacional em um determinado
período de tempo, em que P é a população em milhares de habitantes e t é o número de anos desde
1980.
Qual a taxa média de crescimento populacional anual dessa cidade?
(A) 1,023%
(B) 1,23%
(C) 2,3%
(D) 0,023%
(E) 0,23%
03. (Polícia Civil/SP – Desenhista Técnico-Pericial – VUNESP) Uma população P cresce em função
do tempo t (em anos), segundo a sentença 𝑷 = 𝟐𝟎𝟎𝟎 . 𝟓𝟎,𝟏 .𝒕
. Hoje, no instante t = 0, a população é de 2
000 indivíduos. A população será de 50 000 indivíduos daqui a
(A) 20 anos.
(B) 25 anos.
(C) 50 anos.
(D) 15 anos.
(E) 10 anos.

140
04. (IF/BA – Pedagogo – IF/BA) Em um período longo de seca, o valor médio de água presente em
um reservatório pode ser estimado de acordo com a função: Q(t) = 4000 . 2-0,5 . t
, onde t é medido em
meses e Q(t) em metros cúbicos. Para um valor de Q(t) = 500, pode-se dizer que o valor de t é:
(A) 6 meses
(B) 8 meses
(C) 5 meses
(D) 10 meses
(E) 4 meses
05. (CBTU - Assistente Operacional - FUMARC) Uma substância se decompõe segundo a lei Q(t)
= K.2 – 0,5 t
, sendo K uma constante, t é o tempo medido em minutos e Q(t) é a quantidade de
substância medida em gramas no instante t. O gráfico a seguir representa os dados desse processo
de decomposição. Baseando-se na lei e no gráfico de decomposição dessa substância,
é CORRETO afirmar que o valor da constante K e o valor de a (indicado no gráfico)
são, respectivamente, iguais a:
(A) 2048 e 4
(B) 1024 e 4
(C) 2048 e 2
(D) 1024 e 2
(E) 1024 e 8
Comentários
01. Resposta: A
Como o expoente é um número negativo (- x), basta invertemos a fração para deixa-lo positivo, ou
seja:
(13)-x
= (31)x
= 3x
, e está função é fácil identificar que será crescente, pois se aumentarmos o valor
de x, aumentamos o valor de f(x).
02. Resposta: C
𝑃(𝑡) = 234 . (1,023)𝑡
Primeiramente, vamos calcular a população inicial, fazendo t = 0:
𝑃(0) = 234 . (1,023)0
= 234 . 1 = 234 mil
Agora, vamos calcular a população após 1 ano, fazendo t = 1:
𝑃(1) = 234 . (1,023)1
= 234 . 1,023 = 239,382
Por fim, vamos utilizar a Regra de Três Simples:
População %
234 --------------- 100
239,382 ------------ x
234.x = 239,382 . 100
x = 23938,2 / 234
x = 102,3%
102,3% = 100% (população já existente) + 2,3% (crescimento)

141
03. Resposta: A
50000 = 2000 . 50,1 .𝑡
50,1 .𝑡
=
50000
2000
50,1 .𝑡
= 52
Vamos simplificar as bases (5), sobrando somente os expoentes. Assim:
0,1 . t = 2
t = 2 / 0,1
t = 20 anos
04. Resposta: A
500 = 4000 * 2-0.5t
500/4000 = 2 -0.5t
simplificando,
1/8 = 2 -0.5t
deixando o expoente positivo, invertemos a base:
1/8 = 1/2 0.5t
(½)3
= (½)0,5t
0,5t = 3
t = 3/0,5 = 6.
05. Resposta: A
Calcular o valor de K, ou seja, o valor inicial
Q(t) = K . 2-0,5t
. Perceba que o K ocupa a posição referente à quantidade inicial, t=0. Q(t) = 2048
Assim, temos para o ponto (0, 2048), temos tempo zero e quantidade final 2048.
Calcular o valor de a, o seja, o tempo quando a quantidade final for 512.
Quantidade final = quantidade inicial x (crescimento)período
512 = 2048 x (2)-0,5t
512 = 2048 x (2)-0,5t
512/2048 = (2)-0,5t
¼ = (2)-0,5t
(1/2)2
= (1/2)0,5t
0,5t = 2
t = 2/0,5 = 4
Assim temos 2048 e 4.
FUNÇÃO LOGARÍTMICA
Toda equação que contém a incógnita na base ou no logaritmando de um logaritmo é denominada
equação logarítmica. Abaixo temos alguns exemplos de equações logarítmicas:
log2 𝑥 = 3
log𝑥 100 = 2
7log5 625𝑥 = 42
3log2𝑥 64 = 9
log−6−𝑥 2𝑥 = 1
Perceba que nestas equações a incógnita encontra-se ou no logaritmando, ou na base de um
logaritmo. Para solucionarmos equações logarítmicas recorremos a muitas das propriedades dos
logaritmos.
Função Logarítmica
O estudo dos gráficos das funções envolvidas auxilia na resolução de equações ou inequações, pois
as operações algébricas a serem realizadas adquirem um significado que é visível nos gráficos das
funções esboçados no mesmo referencial cartesiano.
Função logarítmica de base a, é toda função f : R*+ → R, definida por 𝑓(𝑥) = log𝑎 𝑥 com:
a ϵ R*+ e a ≠ 1.

142
Podemos observar neste tipo de função que a variável independente x é um logaritmando, por isto a
denominamos função logarítmica. Observe que a base a é um valor real constante, não é uma variável,
mas sim um número real.
A função logarítmica de R*+ → R é inversa da função exponencial de R*+ → R e vice-versa, pois:
log𝑏 𝑎 = 𝑥 ⟺ 𝑏𝑥
= 𝑎
Representação da Função Logarítmica no Plano Cartesiano
Podemos representar graficamente uma função logarítmica da mesma forma que fizemos com a
função exponencial, ou seja, escolhendo alguns valores para x e montando uma tabela com os
respectivos valores de f(x). Depois localizamos os pontos no plano cartesiano e traçamos a curva do
gráfico. Vamos representar graficamente a função 𝑓(𝑥) = log 𝑥 e como estamos trabalhando com um
logaritmo de base 10, para simplificar os cálculos vamos escolher para x alguns valores que são potências
de 10:
0,001, 0,01, 0,1, 1 e 10.
Temos então seguinte a tabela:
x y = log x
0,001 y = log 0,001 = -3
0,01 y = log 0,01 = -2
0,1 y = log 0,1 = -1
1 y = log 1 = 0
10 y = log 10 = 1
Acima temos o gráfico desta função logarítmica, no qual localizamos cada um dos pontos obtidos da
tabela e os interligamos através da curva da função: Veja que para valores de y < 0,01 os pontos estão
quase sobre o eixo das ordenadas, mas de fato nunca chegam a estar. Note também que neste tipo de
função uma grande variação no valor de x implica numa variação bem inferior no valor de y. Por exemplo,
se passarmos de x = 100 para x = 1 000 000, a variação de y será apenas de 2 para 6. Isto porque:
{
𝑓(100) = log 100 = 2
𝑓(1000000) = log 1000000 = 6
Função Crescente e Decrescente
Assim como no caso das funções exponenciais, as funções logarítmicas também podem ser
classificadas como função crescente ou função decrescente. Isto se dará em função da base a ser maior
ou menor que 1. Lembre-se que segundo a definição da função logarítmica f:R*+ → R, definida por 𝑓(𝑥) =
log𝑎 𝑥 , temos que a > 0 e a ≠ 1.

143
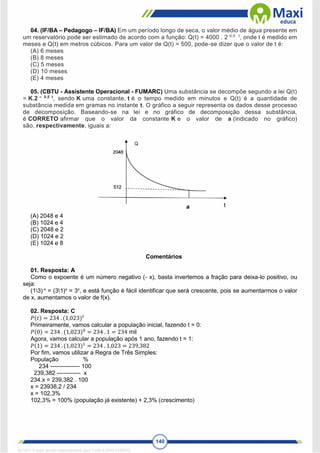
Função Logarítmica Crescente
Se a > 1 temos uma função logarítmica crescente, qualquer que seja o valor real positivo de x. No
gráfico da função ao lado podemos observar que à medida que x aumenta, também aumenta f(x) ou y.
Graficamente vemos que a curva da função é crescente. Também podemos observar através do gráfico,
que para dois valores de x (x1 e x2), que log𝑎 𝑥2 > log𝑎 𝑥1 ⟺ 𝑥2 > 𝑥1, isto para x1, x2 e a números reais
positivos, com a > 1.
Função Logarítmica Decrescente
Se 0 < a < 1 temos uma função logarítmica decrescente em todo o domínio da função. Neste outro
gráfico podemos observar que à medida que x aumenta, y diminui. Graficamente observamos que a curva
da função é decrescente. No gráfico também observamos que para dois valores de x (x1 e x2), que
log𝑎 𝑥2 < log𝑎 𝑥1 ⟺ 𝑥2 > 𝑥1 , isto para x1, x2 e a números reais positivos, com 0 < a < 1. É importante
frisar que independentemente de a função ser crescente ou decrescente, o gráfico da função sempre
cruza o eixo das abscissas no ponto (1, 0), além de nunca cruzar o eixo das ordenadas e que o log𝑎 𝑥2 =
log𝑎 𝑥1 ⟺ 𝑥2 = 𝑥1, isto para x1, x2 e a números reais positivos, com a ≠ 1.
A função logaritmo natural mais simples é a função y = f0(x) = lnx. Cada ponto do gráfico é da forma
(x, lnx) pois a ordenada é sempre igual ao logaritmo natural da abscissa.
O domínio da função ln é R*+=]0,∞[ e a imagem é o conjunto R=]-∞,+∞[.
O eixo vertical é uma assíntota ao gráfico da função. De fato, o gráfico se aproxima cada vez mais da
reta x = 0.
O que queremos será descobrir como é o gráfico de uma função logarítmica natural geral, quando
comparado ao gráfico de y = ln x, a partir das transformações sofridas por esta função.

144
Consideremos uma função logarítmica cuja expressão é dada por y = f1(x) = ln x + k, onde k é uma
constante real. A pergunta natural a ser feita é, qual a ação da constante k no gráfico dessa nova função
quando comparado ao gráfico da função inicial y = f0(x) = ln x?
Ainda podemos pensar numa função logarítmica que seja dada pela expressão y = f2(x) = a.ln x onde
a é uma constante real, a 0.
Observe que se a = 0, a função obtida não será logarítmica, pois será a constante real nula. Uma
questão que ainda se coloca é a consideração de funções logarítmicas do tipo y = f3(x) = ln(x + m), onde
m é um número real não nulo. Se g(x) = 3.ln(x - 2) + 2/3, desenhe seu gráfico, fazendo os gráficos
intermediários, todos num mesmo par de eixos.
y = a.ln(x + m) + k
Conclusão: Podemos, portanto, considerar funções logarítmicas do tipo y = f4(x) = a In (x + m) + k,
onde o coeficiente a não é zero, examinando as transformações do gráfico da função mais simples y = f0
(x) = In x, quando fazemos, em primeiro lugar, y = ln(x + m); em seguida, y = a.ln(x + m) e, finalmente, y
= a.ln(x + m) + k.
Analisemos o que aconteceu:
- Em primeiro lugar, y = ln(x + m) sofreu uma translação horizontal de -m unidades, pois x = - m exerce
o papel que x = 0 exercia em y = ln x;
- A seguir, no gráfico de y = a.ln(x + m) ocorreu mudança de inclinação pois, em cada ponto, a ordenada
é igual àquela do ponto de mesma abscissa em y = ln(x + m) multiplicada pelo coeficiente a;
- Por fim, o gráfico de y = a.ln(x + m) + k sofreu uma translação vertical de k unidades, pois, para cada
abscissa, as ordenadas dos pontos do gráfico de y = a.ln(x + m) + k ficaram acrescidas de k, quando
comparadas às ordenadas dos pontos do gráfico de y = a.ln(x + m).
Questões
01. (PETROBRAS - Geofísico Junior - CESGRANRIO) Se log x representa o logaritmo na base 10
de x, então o valor de n tal que log n = 3 - log 2 é:
(A) 2000
(B) 1000
(C) 500
(D) 100
(E) 10
02. (MF – Assistente Técnico Administrativo – ESAF) Sabendo-se que log x representa o logaritmo
de x na base 10, calcule o valor da expressão log 20 + log 5.
(A) 5
(B) 4
(C) 1
(D) 2
(E) 3
03. (SEE/AC – Professor – FUNCAB) Assinale a alternativa correta, considerando a função a seguir.
(A) O domínio da função é o conjunto dos números reais.
(B) O gráfico da função passa pelo ponto (0, 0).
(C) O gráfico da função tem como assíntota vertical a reta x = 2.
(D) Seu gráfico toca o eixo Y.
(E) Seu gráfico toca o eixo X em dois pontos distintos.
04. (PETROBRAS - Analista de Comercialização e Logística Júnior - CESGRANRIO) Ao resolver
um exercício, um aluno encontrou as expressões 8p
= 3 e 3q
= 5. Quando perguntou ao professor se suas
expressões estavam certas, o professor respondeu que sim e disse ainda que a resposta à pergunta era
dada por

145
Se log x representa o logaritmo na base 10 de x, qual é a resposta correta, segundo o professor?
(A)log 8
(B)log 5
(C)log 3
(D)log 2
(E)log 0,125
05. (TRT 13ª Região - Analista Judiciário - FCC) Com base em um levantamento histórico e utilizando
o método dos mínimos quadrados, uma empresa obteve a equação para estimar a
probabilidade (p) de ser realizada a venda de determinado equipamento em função do tempo (t), em
minutos, em que as propriedades do equipamento são divulgadas na mídia. Considerando que ln (0,60)
= - 0,51, tem-se que se as propriedades do equipamento forem divulgadas por um tempo de 15 minutos
na mídia, então a probabilidade do equipamento ser vendido é, em %, de
Observação: ln é o logaritmo neperiano tal que ln(e) = 1.
(A)62,50
(B)80,25.
(C) 72,00.
(D)75,00.
(E)64,25.
06. (PETROBRAS - Conhecimentos Básicos - CESGRANRIO) Quanto maior for a profundidade de
um lago, menor será a luminosidade em seu fundo, pois a luz que incide em sua superfície vai perdendo
a intensidade em função da profundidade do mesmo. Considere que, em determinado lago, a intensidade
y da luz a x cm de profundidade seja dada pela função y = i0 . ( 0,6 )x/88
, onde i0 representa a intensidade
da luz na sua superfície. No ponto mais profundo desse lago, a intensidade da luz corresponde a i0/3
A profundidade desse lago, em cm, está entre.
Dados
log 2 = 0,30
log 3 = 0,48
(A)150 e 160
(B)160 e 170
(C)170 e 180
(D)180 e 190
(E)190 e 200
07. (DNIT - Analista em Infraestrutura de Transportes - ESAF) Suponha que um técnico efetuou
seis medições de uma variável V1, cujos dados são mostrados na tabela abaixo. Ao perceber que os
valores cresciam de forma exponencial, o técnico aplicou uma transformação matemática (logaritmo na
base 10) para ajustar os valores originais em um intervalo de valores menor. A referida transformação
logarítmica vai gerar novos valores cujo intervalo varia de:
(A) 0 a 1.
(B)0 a 5.
(C)0 a 10.
(D)0 a 100.
(E)1 a 6.

146
08. (PETROBRAS - Técnico de Exploração de Petróleo Júnior - CESGRANRIO) Se y = log81 (1
⁄27)
e x ∈ IR+ são tais que xy
= 8 , então x é igual a
(A)1
⁄16
(B)1
⁄2
(C)log38
(D) 2
(E)16
09. (PETROBRAS - Geofísico Junior - CESGRANRIO) Se log x representa o logaritmo na base 10
de x, então o valor de n tal que log n = 3 - log 2 é
(A)2000
(B)1000
(C)500
(D)100
(E)10
10. (PETROBRAS - Todos os Cargos - CESGRANRIO) Em calculadoras científicas, a tecla log serve
para calcular logaritmos de base 10. Por exemplo, se digitamos 100 e, em seguida, apertamos a tecla log,
o resultado obtido é 2. A tabela a seguir apresenta alguns resultados, com aproximação de três casas
decimais, obtidos por Pedro ao utilizar a tecla log de sua calculadora científica.
Utilizando-se os valores anotados por Pedro na tabela acima, a solução da equação log6+x=log28 é
(A)0,563
(B)0,669
(C)0,966
(D)1,623
(E)2,402
Comentários
01. Resposta: C
log n = 3 - log 2
log n + log 2 = 3 . 1
onde 1 = log 10 então:
log (n . 2) = 3 . log 10
log(n . 2) = log 103
2n = 103
2n = 1000
n = 1000 / 2
n = 500
02. Resposta: D
E = log20 + log5
E = log(2 x 10) + log5
E = log2 + log10 + log5
E = log10 + log (2 x 5)
E = log10 + log10
E = 2 log10
E = 2
03. Resposta: C
(x) = log2(x - 2)
Verificamos a condição de existência, daí x – 2 > 0

147
X > 2
Logo a reta x = 2 é uma assíntota vertical.
04. Resposta: B
8p
= 3
23
p = 3
log23p
= log3
3p = (log3/log2)
p = (log3/log2).1/3
3q
= 5
q.log3 = log5
q = log5/log3
3.p.q = 3. (log3/log2).1/3 . log5/log3 = log5/log2
3.p.q/(1 + 3.p.q)
log5/log2/(1 + log5/log2)
(log5/log2)/( log2/log2 + log5/log2)
(log5/log2)/(log2 + log5)/log2)
(log5/log2)/( log10)/log2)
(log5/ log10)=
log5
05. Resposta: A
Como sabemos que ln (0,60) = -0,51
então ln (1 / 0,60) = 0,51
Substituindo t = 15 minutos em 0,06 + 0,03 . t, teremos 0,06 + 0,03*15 = 0,51
logo 1 / 0,60 = p / (1 - p)
1 - p = 0,60 . p
p = 0,625
06. Resposta: E
onde y = i0
. 0,6 (x/88)
então:
i0
/ 3 = i0
.0,6 (x/88)
(i / 3) . (1/ i) = 0,6 (x/88)
1/3 = 0,6 (x/88)
log 1/3 = log 0,6 (x/88)
log 1 - log 3 = x/88 . log 6/10
0 - 0,48 = x/88 . log 6/10
88 . (- 0,48) = x . [ log 6 - log 10 ]
6 = 3 . 2 ===> log 3 + log 2
como log10 na base 10 = 1.
- 42,24 = x . [ log 3 + log 2 - (1)]
- 42,24 = x . [ 0,48 + 0,30 - 1 ]
x = - 42,24 / - 0,22
x = (42,24 / 0,22) = 192
x = 192 cm
07. Resposta: B
A transformação logarítmica vai gerar novos valores, através dos seguintes cálculos:
medida 1 = log 1 = 0
medida 4 = log 1000 = 3
medida 5 = log 10000 = 4
medida 6 = log 100000 = 5
logo os valores (1,10,100,1000,10000,100000) transformados em logaritmos reduziu o intervalo de
valores para (0,1,2,3,4,5), ou seja, 0-5.

148
08. Resposta: A
y = log (81) (1/27)
y = -3log(81)(3)
y = -3. 1/4
y = -3/4
x(-3/4)
= 8
Elevando os dois termos à quarta potência:
x-3
= 84
1/x3
= 84
Agora raiz cubica dos dois termos:
1/x = 8 4/3
Como 3
√8=2
1/x = 24
1/x = 16
x = 1/16
09. Resposta: C
De acordo com o enunciado:
log n = 3 - log 2
log n + log 2 = 3 . 1,
onde 1 = log 10
então:
log (n . 2) = 3 . log 10
log(n . 2) = log 10 3
2n = 103
2n = 1000
n = 1000 / 2
n = 500
10. Resposta: B
Log 6 = Log (2 . 3)
De acordo com uma das propriedades:
Log (A . B) = Log A + Log B
Então, Log (2 . 3) = Log 2 + Log 3.
Fatorando o número 28 temos que
28=2x2x7
Temos que:
Log 28 = Log (2x2x7)
ou seja,
Log 28 = Log 2 + Log 2 + Log 7
Portanto:
Log 2 + Log 3 + x = Log 2 + Log 2 + Log 7
Cortando o Log 2 dos dois lados temos:
Log 3 + x = Log 2 + Log 7
Dados os valores da tabela, e substituindo-os, temos que:
0,477 + x = 0,301 + 0,845
x = 0,669
MATRIZES
Em jornais, revistas e na internet vemos frequentemente informações numéricas organizadas em
tabelas, colunas e linhas. Exemplos:
7 - Matrizes.

149
Em matemática essas tabelas são exemplos de matrizes16
. O crescente uso dos computadores tem
feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia,
Matemática, Física, dentre outras.
Definição
Seja m e n números naturais não nulos. Uma matriz do tipo m x n, é uma tabela de m.n números reais
dispostos em m linhas e n colunas.
Exemplo:
Um elemento qualquer dessa matriz será representado pelo símbolo: aij, no qual o índice i refere-se à
linha, o índice j refere-se à coluna em que se encontram tais elementos. As linhas são enumeradas de
cima para baixo e as colunas, da esquerda para direita.
Exemplo
Representamos uma matriz colocando seus elementos (números) entre parêntese ou colchetes ou
também (menos utilizado) duas barras verticais à esquerda e direita.
16
FILHO, Begnino Barreto; SILVA,Claudio Xavier da – Matemática – Volume Único - FTD
mundoeducacao.bol.uol.com.br/matematica/equacoes-envolvendo-matrizes.html

150
Exemplos
𝐴 = (5 −1
1
2
) é 𝑢𝑚𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 1 𝑥 3
𝐵 = [
7 −2
3 4
] é 𝑢𝑚𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 2 𝑥 2
𝐶 = ‖
√5 1/3 1
7 2 −5
−4 1/5 2
‖ é 𝑢𝑚𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 3 𝑥 3
𝐷 = [
−1 5 8
−1 2 −3
] é 𝑢𝑚𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 2 𝑥 3
Exemplo
Escrever a matriz A = (aij)2 x 3, em que aij = i – j
A matriz é do tipo 2 x 3 (duas linhas e três colunas), podemos representa-la por:
Matrizes Especiais
Algumas matrizes recebem nomes especiais. Vejamos:
- Matriz Linha: é uma matriz formada por uma única linha.
Exemplo
𝐴 = [1 7 −5] , 𝑚𝑎𝑡𝑟𝑖𝑧 𝑙𝑖𝑛ℎ𝑎 1𝑥3
- Matriz coluna: é uma matriz formada por uma única coluna.
Exemplo
𝐵 = [
1
−5
7
] , 𝑚𝑎𝑡𝑟𝑖𝑧 𝑐𝑜𝑙𝑢𝑛𝑎 3𝑥1
- Matriz nula: é matriz que possui todos os elementos iguais a zero.
Exemplo
𝐶 = (
0 0
0 0
0 0
) , 𝑚𝑎𝑡𝑟𝑖𝑧 𝑛𝑢𝑙𝑎 3𝑥2
- Matriz quadrada: é a matriz que possui o número de linhas igual ao número de colunas. Podemos,
neste caso, chamar de matriz quadrada de ordem n.
Exemplo
𝐷 = (
3 2
−4 1
) , 𝑚𝑎𝑡𝑟𝑖𝑧 2𝑥2 𝑜𝑢 𝑚𝑎𝑡𝑟𝑖𝑧 𝑞𝑢𝑎𝑑𝑟𝑎𝑑𝑎 𝑑𝑒 𝑜𝑟𝑑𝑒𝑚 2.

151
A diagonal principal de D é formada pelos elementos cujo índice é igual ao índice da coluna (a11 e a22).
A outra diagonal recebe o nome de diagonal secundária de D.
- Matriz identidade: é a matriz quadrada em que cada elemento da diagonal principal é igual a 1, e os
demais têm o valor 0. Representamos a matriz identidade pela seguinte notação: In.
Exemplos
Também podemos definir uma matriz identidade da seguinte forma:
𝐼𝑛 = [𝑎𝑖𝑗]𝑛 𝑥 𝑛
, 𝑜𝑛𝑑𝑒 {
𝑎𝑖𝑗 = 1, 𝑠𝑒 𝑖 = 𝑗
𝑎𝑖𝑗 = 0, 𝑠𝑒 𝑖 ≠ 𝑗
- Matriz transposta: é a matriz onde as linhas são ordenadamente iguais a colunas desta mesma
matriz e vice e versa. Ou seja:
Dada uma matriz A de ordem m x n, chama-se matriz transposta de A, indicada por At, a matriz cuja a
ordem é n x m, sendo as suas linhas ordenadamente iguais às colunas da matriz A.
Exemplo
𝐴 = [
2 −1
7 10
] , 𝑒𝑛𝑡ã𝑜 𝐴𝑡
= [
2 7
− 10
]
Observe que:
- a 1ª linha da matriz A é igual à 1ª coluna da matriz At
.
- a 2ª linha da matriz A é igual a 2ª coluna da matriz At
.
Generalizando, temos:
- Matriz oposta: é a matriz obtida a partir de A, trocando-se o sinal de todos os seus elementos.
Representamos por - A tal que A + (- A) = O, em que O é a matriz nula do tipo m x n.
Exemplo

152
- Matriz simétrica: é uma matriz quadrada cujo At
= A; ou ainda aij = aji
Exemplo
- Matriz antissimétrica: é uma matriz quadrada cujo At
= - A; ou ainda aij = - aij.
Exemplo
Classificação de Acordo com os Elementos da Matriz
- Real: se todos os seus elementos são reais.
Exemplo
𝐴 = [
1 −5
3 2
]
- Imaginária: se pelo menos um dos seus elementos é complexo.
Exemplo
𝐵 = [
1 −5
3 𝑖
]
- Triangular superior: é uma matriz quadrada em que os elementos abaixo da diagonal principal são
nulos.
Exemplo
- Triangular inferior: é uma matriz quadrada em que os elementos acima da diagonal principal são
nulos.
Exemplo

153
Igualdade de Matrizes
Dizemos que duas matrizes A e B, de mesma ordem, são iguais (A = B) se, e somente se, os seus
elementos de mesma posição forem iguais, ou seja:
A = [aij] m x n e B = [bij] p x q
Sendo A = B, temos:
m = p e n = q
Operações com Matrizes
- Adição: a soma de duas matrizes A e B de mesma ordem é matriz também de mesma ordem, obtida
com a adição dos elementos de mesma posição das matrizes A e B.
Exemplo
Propriedades: considerando as matrizes de mesma ordem, algumas propriedades são válidas:
Comutativa: A + B = B + A
Associativa: A + (B + C) = (A + B) + C
Elemento simétrico: A + (-A) = 0
Elemento neutro: A + 0 = A
- Subtração: a diferença entre duas matrizes A e B, de mesma ordem, é a matriz obtida pela adição
da matriz A com a oposta da matriz B, ou seja:
Exemplo
- Multiplicação de um número real por uma matriz: o produto de um número real k por uma matriz
A, é dado pela multiplicação de cada elemento da matriz A por esse número real k.

154
Exemplo
- Multiplicação de matrizes: para multiplicarmos duas matrizes A e B só é possível mediante a uma
condição e uma técnica mais elaborada. Vejamos:
Condição: o número de COLUNAS da A (primeira) têm que ser igual ao número de LINHAS de B
(segunda).
Logo a ordem da matriz resultante é a LINHA de A e a COLUNA DE B.
Técnica: Multiplicamos o 1º elemento da LINHA 1 de A pelo 1º elemento da primeira COLUNA de B,
depois o 2º elemento da LINHA 1 de A pelo 2º elemento da primeira COLUNA de B e somamos esse
produto. Fazemos isso sucessivamente, até termos efetuado a multiplicação de todos os termos.
Exemplo
A matriz C é o resultado da multiplicação de A por B.
Propriedades da multiplicação: admite-se as seguintes propriedades
Associativa: (A.B). C = A.(B.C)
Distributiva: (A + B). C = A. C + B. C e C. (A + B) = C. A + C. B
Observação: a propriedade comutativa NÂO é válida na multiplicação de matrizes, pois geralmente
A.B ≠ B.A
Matriz Inversa
Dizemos que uma matriz é inversa A–1
(toda matriz quadrada de ordem n), se e somente se, A.A-1
= In
e A-1
.A = In ou seja:
𝑨. 𝑨−𝟏
= 𝑨−𝟏
. 𝑨 = 𝑰𝒏 , 𝑜𝑛𝑑𝑒 {
𝐴 é 𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑑𝑎𝑑𝑎.
𝐴−1
é 𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑖𝑛𝑣𝑒𝑟𝑠𝑎 𝑑𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝐴.
𝐼𝑛 é 𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑖𝑑𝑒𝑛𝑡𝑖𝑑𝑎𝑑𝑒 𝑑𝑒 𝑚𝑒𝑠𝑚𝑎 𝑜𝑟𝑑𝑒𝑚 𝑑𝑒 𝐴.
Exemplos
1) A matriz 𝐵 = [
8 −2
3 −1
] é inversa da matriz 𝐴 = [
1
2
−1
3
2
−4
] , pois:

155
2) Vamos verificar se a matriz 𝐴 = (
2 5
1 3
) 𝑒 𝐵 = (
1 2
1 1
) , são inversas entre si:
Portanto elas, não são inversas entre si.
3) Dada a matriz 𝐴 = [
2 1
3 2
], determine a inversa, A-
¹.
Vamos então montar a matriz 𝐴−1
= [
𝑎 𝑏
𝑐 𝑑
] , 𝑡𝑒𝑚𝑜𝑠 𝑞𝑢𝑒 𝐴. 𝐴−1
= 𝐼𝑛
[
2 1
3 2
] . [
𝑎 𝑏
𝑐 𝑑
] = [
1 0
0 1
] → [
2𝑎 + 𝑐 2𝑏 + 𝑑
3𝑎 + 2𝑐 3𝑏 + 2𝑑
] = [
1 0
0 1
]
Fazendo as igualdades temos:
{
2𝑎 + 𝑐 = 1
3𝑎 + 2𝑐 = 0
{
2𝑏 + 𝑑 = 0
3𝑏 + 2𝑑 = 1
Resolvendo os sistemas temos: a = 2; b = -1; c = -3 e d = 2
Então a matriz inversa da matriz A é:
𝐴−1
= [
2 −1
−3 2
]
Equação Matricial
No caso das equações com matrizes (equações matriciais), elas são equações cujas incógnitas são
matrizes.
Vejamos um exemplo:
Encontre a matriz X da equação 2.A+B=X, sabendo que:
Neste exemplo, a incógnita já estava isolada.
Vejamos um exemplo em que a incógnita não está isolada na equação. Nestes casos devemos tomar
cuidado ao operarmos as matrizes de um lado para o outro da igualdade.
Exemplo:
Resolva a equação a seguir: X+B=2A, utilizando as mesmas matrizes do exemplo anterior.
Antes de substituirmos as matrizes, façamos o isolamento da incógnita, lembrando sempre das
propriedades das operações das matrizes.

156
Note que não passamos a matriz B para o outro lado da igualdade; na verdade operamos a matriz
oposta de B (matriz -B) dos dois lados.
Devemos tomar esse cuidado, pois quando nos depararmos com produto de matrizes, não poderemos
passar a matriz para o outro lado dividindo; deveremos operar a matriz inversa dos dois lados.
O diferencial das equações que conhecíamos para as equações com matrizes está nesse maior
cuidado ao isolarmos a incógnita.
Voltando à resolução da equação, temos que substituir os valores das matrizes A e B na equação.
Sendo assim:
Questões
01. (Pref. do Rio de Janeiro/RJ - Professor - Pref. do Rio de Janeiro) Considere as matrizes A
e B, a seguir.
O elemento que ocupa a terceira linha e a segunda coluna da matriz produto BA vale:
(A) 9
(B) 0
(C) – 9
(D) – 11
02. (BRDE – Analista de Sistemas – FUNDATEC) Considere as seguintes matrizes: 𝐴 =
[
2 3
4 6
] , 𝐵 = [
2 3
4 5
6 6
] 𝑒 𝐶 = [
2 1 0
4 6 7
], a solução de C x B + A é:
(A) Não tem solução, pois as matrizes são de ordem diferentes.
(B) [
10 14
78 90
]
(C) [
2 3
4 5
]
(D) [
6 6
20 36
]
(E) [
8 11
74 84
]
03. (PM/SE – Soldado 3ª Classe – FUNCAB) A matriz abaixo registra as ocorrências policiais em uma
das regiões da cidade durante uma semana.
Sendo M=(aij)3x7 com cada elemento aij representando o número de ocorrência no turno i do dia j da
semana.

157
O número total de ocorrências no 2º turno do 2º dia, somando como 3º turno do 6º dia e com o 1º turno
do 7º dia será:
(A) 61
(B) 59
(C) 58
(D) 60
(E) 62
04. (CPTM – ANALISTA DE COMUNICAÇÃO JÚNIOR – MAKIYAMA) Para que a soma de uma
matriz 𝐴 = [
𝑎 𝑏
𝑐 𝑑
] e sua respectiva matriz transposta At
em uma matriz identidade, são condições a serem
cumpridas:
(A) a=0 e d=0
(B) c=1 e b=1
(C) a=1/c e b=1/d
(D) a²-b²=1 e c²-d²=1
(E) b=-c e a=d=1/2
05. (CPTM – ALMOXARIFE – MAKIYAMA) Assinale a alternativa que apresente o resultado da
multiplicação das matrizes A e B abaixo:
𝐴 = (
2 1
3 −1
) ∙ 𝐵 = (
0 4 −2
1 −3 5
)
(A) (
−1 −5 1
1 15 11
)
(B) (
1 5 1
−1 15 − 11
)
(C) (
1 5 − 1
1 −15 11
)
(D) (
1 5 1
1 15 11
)
(E) (
−1 5 − 1
1 15 − 11
)
06. (PM/SP – SARGENTO CFS – CETRO) Considere a seguinte sentença envolvendo matrizes:
(
6 𝑦
7 2
) + (
1 −3
8 5
) = (
7 7
15 7
)
Diante do exposto, assinale a alternativa que apresenta o valor de y que torna a sentença verdadeira.
(A) 4.
(B) 6.
(C) 8.
(D) 10.
Comentários
01. Resposta: D
Como as matrizes são quadradas de mesma ordem, podemos então multiplica-las:
𝐵. 𝐴 = [
5 −2 0
−1 2 4
−3 −2 1
] . [
1 2 −2
−1 3 0
2 1 3
] →
[
5.1 + (−2). (−1) + 0.2 5.2 + (−2). 3 + 0.1 5. (−2) + (−2). 0 + 0.3
−1.1 + 2. (−1) + 4.2 −1.2 + 2.3 + 4.1 −1. (−2) + 2.0 + 4.3
−3.1 + (−2). (−1) + 1.2 −3.2 + (−2). 3 + 1.1 −3. (−2) + (−2). 0 + 1.3
] = [
7 4 −10
5 8 14
1 −11 9
]
Logo o elemento que ocupa a terceira linha e a segunda coluna é o -11.

158
02. Resposta: B
Vamos ver se é possível multiplicar as matrizes.
C(2x3) e B(3x2), como o número de colunas de C é igual ao número de colunas de B, logo é possível
multiplicar, o resultado será uma matriz 2x2(linha de C e coluna de B):
𝐶 𝑥𝐵 = [
2 1 0
4 6 7
] . [
2 3
4 5
6 6
] → [
2.2 + 1.4 + 0.6 2.3 + 1.5 + 0.6
4.2 + 6.4 + 7.6 4.3 + 6.5 + 7.6
] = [
8 11
74 84
]
Agora vamos somar a matriz A(2x2) a matriz resultante da multiplicação que também tem a mesma
ordem:
[
8 11
74 84
] + 𝐴 = [
8 11
74 84
] + [
2 3
4 6
] → [
8 + 2 11 + 3
74 + 4 84 + 6
] = [
10 14
78 90
]
03. Resposta: E
Turno i –linha da matriz
Turno j- coluna da matriz
2º turno do 2º dia – a22=18
3º turno do 6º dia-a36=25
1º turno do 7º dia-a17=19
Somando:18+25+19=62
04. Resposta: E
𝐴 + 𝐴𝑡
= [
𝑎 𝑏
𝑐 𝑑
] + [
𝑎 𝑐
𝑏 𝑑
] = [
2𝑎 𝑏 + 𝑐
𝑏 + 𝑐 2𝑑
] = [
1 0
0 1
]
2a =1 → a =1/2 → b + c = 0 → b = -c
2d=1
D=1/2
05. Resposta: B
𝐴 ∙ 𝐵 = (
2 ∙ 0 + 1 ∙ 1 2 ∙ 4 + 1 ∙ (−3 ) 2 ∙ (−2) + 1 ∙ 5
3 ∙ 0 + (−1) ∙ 1 3 ∙ 4 + (−1) ∙ (−3) 3 ∙ (−2) + (−1) ∙ 5
)
𝐴 ∙ 𝐵 = (
1 5 1
−1 15 − 11
)
06. Resposta: D
(
6 + 1 = 7 𝑦 − 3 = 7
7 + 8 = 15 2 + 5 = 7
)
y=10
DETERMINANTES
Chamamos de determinante a teoria desenvolvida por matemáticos dos séculos XVII e XVIII, como
Leibniz e Seki Shinsuke Kowa, que procuravam uma fórmula para determinar as soluções de um “Sistema
linear”.
Esta teoria consiste em associar a cada matriz quadrada A, um único número real que denominamos
determinante de A e que indicamos por det A ou colocamos os elementos da matriz A entre duas barras
verticais, como no exemplo abaixo:
8 - Determinantes.

159
Determinante de uma Matriz de Ordem 1
Seja a matriz quadrada de ordem 1: A = [a11]
Chamamos determinante dessa matriz o número:
det A = [ a11] = a11
Exemplos
- A = [-2] → det A = - 2
- B = [5] → det B = 5
- C = [0] → det C = 0
Determinante de uma Matriz de ordem 2
Seja a matriz quadrada de ordem 2:
Chamamos de determinante dessa matriz o número:
Para facilitar a memorização desse número, podemos dizer que o determinante é a diferença entre o
produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária.
Esquematicamente:
Exemplos
Determinante de uma Matriz de Ordem 3
Seja a matriz quadrada de ordem 3:
Chamamos de determinante dessa matriz:

160
Para memorizarmos a definição de determinante de ordem 3, usamos a regra prática denominada
Regra de Sarrus:
- Repetimos a 1ª e a 2ª colunas à direita da matriz.
- Multiplicando os termos entre si, seguindo os traços em diagonal e associando o sinal indicado dos
produtos, temos:
Observação: A regra de Sarrus também pode ser utilizada repetindo a 1ª e 2ª linhas, ao invés de
repetirmos a 1ª e 2ª colunas.
Propriedades
Apresentamos, a seguir, algumas propriedades que visam a simplificar o cálculo dos determinantes:
- Propriedade 1: O determinante de uma matriz A é igual ao de sua transposta At
.
Exemplo
- Propriedade 2: Se B é a matriz que se obtém de uma matriz quadrada A, quando trocamos entre si
a posição de duas filas paralelas, então temos:
detB = - detA
Exemplo
B foi obtida trocando-se a 1ª pela 2ª linha de A.
detA = ad - bc
detB = bc - ad = - (ad - bc) = - detA

161
Assim,
detB = - detA
Consequência da Propriedade 2: Uma matriz A que possui duas filas paralelas “iguais” tem
determinante igual a zero.
Justificativa: A matriz que obtemos de A, quando trocamos entre si as duas filas (linha ou coluna
“iguais”, é igual a A. Assim, de acordo com a propriedade 2, escrevemos que detA = -detA.
Assim: detA = 0
- Propriedade 3: Sendo B uma matriz que obtemos de uma matriz quadrada A, quando multiplicamos
uma de suas filas (linha ou coluna) por uma constante k, então detB = k.detA
Consequência da Propriedade 3: Ao calcularmos um determinante, podemos “colocar em evidência”
um “fator comum” de uma fila (linha ou coluna).
Exemplo
- Sendo A uma matriz quadrada de ordem n, a matriz k. A é obtida multiplicando todos os elementos
de A por k, então:
det(k.A) = kn
.detA
Exemplo
Assim:
det(k.A) = k3
.detA
- Propriedade 4: Se A, B e C são matrizes quadradas de mesma ordem, tais que os elementos
correspondentes de A, B e C são iguais entre si, exceto os de uma fila, em que os elementos de C são
iguais às somas dos seus elementos correspondentes de A e B, então temos:
detC = detA + detB
Exemplos:
- Propriedades 5 (Teorema de Jacobi): O determinante não se altera, quando adicionamos uma fila
qualquer com outra fila paralela multiplicada por um número.

162
Exemplo:
Considere o determinante detA=
Somando a 3ª coluna com a 1ª multiplicada por m, teremos:
Exemplo:
Vamos calcular o determinante D abaixo.
D = 8 + 0 + 0 – 60 – 0 – 0 = -52
Em seguida, vamos multiplicar a 1ª coluna por 2, somar com a 3ª coluna e calcular:
D1 = 48 + 0 + 0 – 100 – 0 – 0 = -52
Observe que D1 = D, de acordo com a propriedade.
Consequência da propriedade 5: Quando uma fila de um determinante é igual à soma de múltiplos
de filas paralelas (combinação linear de filas paralelas), o determinante é igual a zero.
Exemplo:
Seja D=
05
1
4
12
2
3
8
2
1

Observe que cada elemento da 3ª coluna é igual à 1ª coluna multiplicada por 2 somada com a 2ª
coluna multiplicada por 3.

163
8 = 2(1) + 3(2) = 2 + 6
12 = 2(3) + 3(2) = 6 + 6
5 = 2(4) + 3(-1) = 8 - 3
Portanto, pela consequência da propriedade 5, D = 0
Use a regra de Sarrus e verifique.
- Propriedade 6 (Teorema de Binet): Sendo A e B matrizes quadradas de mesma ordem, então:
det(A.B) = detA . detB
Exemplo:
Logo, det(AB) = detA. detB
Consequência da propriedade 6: Sendo A uma matriz quadrada e nN*, temos:
det(Na) = (detA)n
Sendo A uma matriz inversível, temos:
detA-1
=
A
det
1
Justificativa: Seja A matriz inversível.
A-1
. A = I
det(A-1
. A) = det I
detA-1
. detA = det I
detA-1
=
A
det
1
Uma vez que det I = 1, onde i é a matriz identidade.
Determinantes – Teorema de Laplace
- Menor complementar e Cofator: Dada uma matriz quadrada A = (aij)nxn (n2), chamamos menor
complementar do elemento aij e indicamos por Mij o determinante da matriz quadrada de ordem n-1, que
se obtém suprimindo a linha i e a coluna j da matriz A.
Exemplo:
Sendo A=










2
1
2
0
1
4
3
2
1
, temos:
M11=
2
1
0
1
=2
M12=
2
2
0
4
=8
M13=
1
2
1
4
=2

164
Chamamos cofator do elemento aij e indicamos com Aij o número (-1)i+j
.Mij, em que Mij é o menor
complementar de aij.
Exemplo:
Dada uma matriz A=(aij)nxm, com n2, chamamos matriz cofator de A, a matriz cujos elementos são os
cofatores dos elementos de A e indicamos a matriz cofator por cof A. A transposta da matriz cofator de A
é chamada de matriz adjunta de A, que indicamos por adj A.
Exemplo:

165
Determinante de uma Matriz de Ordem n
Vimos até aqui a definição de determinante para matrizes quadradas de ordem 1, 2 e 3.
Seja A uma matriz quadrada de ordem n.
Então:
- Para n = 1
A=[a11] det A=a11
- Para n  2:
ou seja:
detA = a11.A11+a12.A12+…+a1n.A1n
Então, o determinante de uma matriz quadrada de ordem n, n 2 é a soma dos produtos dos
elementos da primeira linha da matriz pelos respectivos cofatores.
Exemplos:
Sendo A= 





22
21
12
11
a
a
a
a
, temos:
detA = a11.A11 + a12.A12, onde:
A11 = (-1)1+1
.|a22| = a22
A12 = (-1)1+2
.|a21| = a21
Assim:
detA = a11.a22 + a12.(-a21)
detA = a11.a22 - a21.a12
Nota: Observamos que esse valor coincide com a definição vista anteriormente.
- Sendo


166
Nota: Observamos que quanto mais “zeros” aparecerem na primeira linha, mais o cálculo é facilitado.
- Teorema de Laplace
Seja A uma matriz quadrada de ordem n, n 2, seu determinante é a soma dos produtos dos
elementos de uma fila (linha ou coluna) qualquer pelos respectivos cofatores.
Exemplo:
Devemos escolher a 4ª coluna para a aplicação do teorema de Laplace, pois, neste caso, teremos que
calcular apenas um cofator.
Observações Importantes: No cálculo do determinante de uma matriz de ordem n, recaímos em
determinantes de matrizes de ordem n-1, e no cálculo destes, recaímos em determinantes de ordem n-2,
e assim sucessivamente, até recairmos em determinantes de matrizes de ordem 3, que calculamos com
a regra de Sarrus, por exemplo.
- O cálculo de um determinante fica mais simples, quando escolhemos uma fila com a maior quantidade
de zeros.
- A aplicação sucessiva e conveniente do teorema de Jacobi pode facilitar o cálculo do determinante
pelo teorema de Laplace.
Exemplo:


167
A 1ª coluna ou 2ª linha tem a maior quantidade de zeros. Nos dois casos, se aplicarmos o teorema de
Laplace, calcularemos ainda três cofatores.
Para facilitar, vamos “fazer aparecer zero” em A31 = -2 e A41 = 3 multiplicando a 1ª linha por 2 e somando
com a 3ª e multiplicando a 1ª linha por -3 e somando com a 4ª linha; fazendo isso, teremos:
Agora, aplicamos o teorema de Laplace na 1ª coluna:
Aplicamos a regra de Sarrus,
det A = (0 – 16 – 21) - ( - 14 + 12 + 0)
detA = 0 – 16 – 21 + 14 – 12 – 0 = -49 + 14
detA = -35
- Aplicação do Teorema de Laplace
Sendo A uma matriz triangular, o seu determinante é o produto dos elementos da diagonal principal;
podemos verificar isso desenvolvendo o determinante de A através da:
- 1ª coluna, se ela for triangular superior;
- através da 1ª linha, se ela for triangular superior;
- através da 1ª linha, se ela for triangular inferior.
Assim:
1ª. A é triangular superior

168
2ª. A é triangular inferior
- Determinante de Vandermonde e Regra de Chió
Uma determinante de ordem n 2 é chamada determinante de Vandermonde ou determinante das
potências se, e somente se, na 1ª linha (coluna) os elementos forem todos iguais a 1; na 2ª, números
quaisquer; na 3ª, os seus quadrados; na 4ª, os seus cubos e assim sucessivamente.
Exemplos:
Determinante de Vandermonde de ordem 3
Determinante de Vandermonde de ordem 4
Os elementos da 2ª linha são denominados elementos característicos.
- Propriedade
Um determinante de Vandermonde é igual ao produto de todas as diferenças que se obtêm subtraindo-
se de cada um dos elementos característicos os elementos precedentes, independente da ordem do
determinante.
Exemplo:
Calcule o determinante;
Sabemos que detA = detAt
, então:


169
Que é um determinante de Vandermonde de ordem 3, então:
detA = (4 – 2).(7 – 2).(7 – 4)=2 . 5 . 3 = 30
Questões
01. (COBRA Tecnologia S-A (BB) - Analista Administrativo - ESPP) O valor de b para que o
determinante da matriz [
𝑥
𝑏
2
2 𝑦
] seja igual a 8, em que x e y são as coordenadas da solução do sistema
{
𝑥 + 2𝑦 = 7
2𝑥 + 𝑦 = 8
, é igual a:
(A) 2.
(B) –2.
(C) 4.
(D) –1.
02. (PM/SP – Sargento Cfs – CETRO) É correto afirmar que o determinante |
1 𝑥
−2 4
|é igual a zero
para x igual a
(A) 1.
(B) 2.
(C) -2.
(D) -1.
03. (CGU – Administrativa – ESAF) Calcule o determinante da matriz:
(
𝑐𝑜𝑠 𝑥 𝑠𝑒𝑛 𝑥
𝑠𝑒𝑛 𝑥 cos 𝑥
)
(A) 1
(B) 0
(C) cos 2x
(D) sen 2x
(E) sen x/2
04. (Pref. Araraquara/SP – Agente da Administração dos Serviços de Saneamento – CETRO)
Dada a matriz 𝐴 = (𝑎𝑖𝑗)3𝑥3
, onde 𝑎𝑖𝑗 = {
2, 𝑠𝑒 𝑖 > 𝑗
−1, 𝑠𝑒 𝑖 ≤ 𝑗
, assinale a alternativa que apresenta o valor do
determinante de A é
(A) -9.
(B) -8.
(C) 0.
(D) 4.
05. (Cobra Tecnologia – Técnico De Operações – Documentos/Qualidade - ESPP) O valor de b
para que o determinante da matriz [
𝑥
𝑏
2
2 𝑦
] seja igual a 8, em que x e y são as coordenadas da solução do
sistema {
𝑥 + 2𝑦 = 7
2𝑥 + 𝑦 = 8
é igual a:
(A) 2.
(B) -2.
(C) 4.
(C) -1.

170
06. (SEAP/PR – Professor de Matemática – PUC/PR) As planilhas eletrônicas facilitaram vários
procedimentos em muitas áreas, sejam acadêmicas ou profissionais. Na matemática, para obter o
determinante de uma matriz quadrada, com um simples comando, uma planilha fornece rapidamente esse
valor. Em uma planilha eletrônica, temos os valores armazenados em suas células:
Para obter o determinante de uma matriz utiliza-se o comando “=MATRIZ.DETERM(A1:D4)” e essa
planilha fornece o valor do determinante:
Se em uma outra planilha forem armazenados os valores representados a seguir,
ao acionar o comando “=MATRIZ.DETERM(A1:C3)” o valor do determinante é:
(A) 1512
(B) 7
(C) 4104
(D) 2376
(E) 8424
07. (TRANSPETRO – Engenheiro Júnior – CESGRANRIO) Um sistema dinâmico, utilizado para
controle de uma rede automatizada, forneceu dados processados ao longo do tempo e que permitiram a
construção do quadro abaixo.
1 3 2 0
3 1 0 2
2 3 0 1
0 2 1 3
A partir dos dados assinalados, mantendo-se a mesma disposição, construiu-se uma matriz M. O valor
do determinante associado à matriz M é
(A) 42
(B) 44
(C) 46
(D) 48
(E) 50
Respostas
01. Resposta: B
{
𝑥 + 2𝑦 = 7 (𝑥 − 2)
2𝑥 + 𝑦 = 8

171
{
−2𝑥 − 4𝑦 = −14
2𝑥 + 𝑦 = 8
- 3y = - 6
y = 2
x = 7 - 2y
x = 7 – 4 = 3
|3
𝑏
2
2 2
| = 8
6 – b = 8
B = - 2
02. Resposta: C
D = 4 - (-2x)
0 = 4 + 2x
x = - 2
03. Resposta: C
det = cos²x - sen²x
det = cos(2x)
04. Resposta: A
𝐴 = (
−1 −1
2 −1
−1
−1
2 2 −1
)
𝐷𝑒𝑡 𝐴 = |
−1 −1
2 −1
−1
−1
2 2 −1
|
detA = - 1 – 4 + 2 - (2 + 2 + 2) = - 9
05. Resposta: B
{
𝑥 + 2𝑦 = 7 (𝑥 − 2)
2𝑥 + 𝑦 = 8
{
−2𝑥 − 4𝑦 = −14
2𝑥 + 𝑦 = 8
Somando as equações:
- 3y = - 6
y = 2
x = 7 – 4 = 3
𝐷𝑒𝑡 = |3
𝑏
2
2 2
|
6 – b = 8
b = - 2
06. Resposta: A
A.B=I
(
1 0 1
2 1 0
0 1 1
) ∙ (
𝑎 𝑏 𝑐
𝑑 𝑒 𝑓
𝑔 ℎ 𝑖
) = (
1 0 0
0 1 0
0 0 1
)

172
(
𝑎 + 𝑔 𝑏 + ℎ 𝑐 + 𝑖
2𝑎 + 2𝑑 2𝑏 + 𝑒 2𝑐 + 𝑓
𝑑 + 𝑔 𝑒 + ℎ 𝑓 + 𝑖
) = (
1 0 0
0 1 0
0 0 1
)
Como queremos saber o elemento da segunda linha e terceira coluna(f):
{
𝑐 + 𝑖 = 0
2𝑐 + 𝑓 = 0
𝑓 + 𝑖 = 1
Da primeira equação temos:
c=-i
substituindo na terceira:
f-c=1
{
2𝑐 + 𝑓 = 0(𝑥 − 1)
𝑓 − 𝑐 = 1
{
−2𝑐 − 𝑓 = 0
𝑓 − 𝑐 = 1
Somando as equações:
-3c=1
C=-1/3
f=2/3
07. Resposta: D
𝑀 = (
1 3 2
3 1 0
2 3 0
0
2
1
0 2 1 3
)
Como é uma matriz 4x4 vamos achar o determinante através do teorema de Laplace. Para isso
precisamos, calcular os cofatores. Dica: pela fileira que possua mais zero. O cofator é dado pela fórmula:
𝐶𝑖𝑗 = (−1)𝑖+𝑗
∙ 𝐷. Para o determinante é usado os números que sobraram tirando a linha e a coluna.
𝐶13 = (−1)4
∙ |
3 1 2
2 3 1
0 2 3
|
𝐶13 = 27 + 8 − 6 − 6 = 23
A13=2.23=46
𝐶43 = (−1)7
|
1 3 0
3 1 2
2 3 1
|
𝐶43 = −(1 + 12 − 6 − 9) = 2
A43=1.2=2
D = 46 + 2 = 48

173
SISTEMAS LINEARES
Um Sistema de Equações Lineares é um conjunto ou uma coleção de equações com as quais é
possível resolver tudo de uma só vez. Sistemas Lineares são úteis para todos os campos da matemática
aplicada, em particular, quando se trata de modelar e resolver numericamente problemas de diversas
áreas. Nas engenharias, na física, na biologia, na química e na economia, por exemplo, é muito comum
a modelagem de situações por meio de sistemas lineares.
Definição
Toda equação do tipo a1x1 + a2x2 + a3x3+...anxn = b, onde a1, a2, a3,.., an e b são números reais e x1, x2,
x3,.., xn são as incógnitas.
Os números reais a1, a2, a3..., an são chamados de coeficientes e b é o termo independente.
Observamos também que todos os expoentes de todas as variáveis são sempre iguais a 1.
Solução de uma equação linear
Na equação 4x – y = 2, o par ordenado (3,10) é uma solução, pois ao substituirmos esses valores na
equação obtemos uma igualdade.
4 . 3 – 10 → 12 – 10 = 2
Já o par (3,0) não é a solução, pois 4.3 – 0 = 2 → 12 ≠ 2
Sistema Linear
Um conjunto de m equações lineares na variáveis x1,x2, ..., xn é dito sistema linear de m equações e n
variáveis.
Dessa forma temos:
𝑎) {
2𝑥 − 3𝑦 = 5
𝑥 + 𝑦 = 4
é 𝑢𝑚 𝑠𝑖𝑠𝑡𝑒𝑚𝑎 𝑐𝑜𝑚 2 𝑒𝑞𝑢𝑎çõ𝑒𝑠 𝑒 2 𝑣𝑎𝑟𝑖á𝑣𝑒𝑖𝑠
𝑏) {
𝑥 − 𝑦 + 𝑧 = 2
−3𝑥 + 4𝑦 = 1
é 𝑢𝑚 𝑠𝑖𝑠𝑡𝑒𝑚𝑎 𝑐𝑜𝑚 2 𝑒𝑞𝑢𝑎çõ𝑒𝑠 𝑒 3 𝑣𝑎𝑟𝑖á𝑣𝑒𝑖𝑠
𝑐){𝑥 − 𝑦 + 2𝑧 − 𝑤 = 0 é 𝑢𝑚 𝑠𝑖𝑠𝑡𝑒𝑚𝑎 𝑐𝑜𝑚 1 𝑒𝑞𝑢𝑎çã𝑜 𝑒 4 𝑣𝑎𝑟𝑖á𝑣𝑒𝑖𝑠
Matrizes associadas a um sistema
Podemos associar a um sistema linear 2 matrizes (completas e incompletas) cujos elementos são os
coeficientes das equações que formam o sistema.
Exemplo:
𝑎) {
4𝑥 + 3𝑦 = 1
2𝑥 − 5𝑦 = −2
Temos que:
𝐴 = (
4 3
2 −5
) é 𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑖𝑛𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎 𝑒 𝐵 = (
4 3
2 −5
1
−2
) é 𝑎 𝑚𝑎𝑡𝑟𝑖𝑧 𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑎.
Solução de um sistema
Dizemos que a1,a2,...,an é a solução de um sistema linear de n variáveis quando é solução de cada
uma das equações do sistema.
Exemplo:
A tripla ordenada (-1,-2,3) é solução do sistema:
9 - Sistemas lineares.

174
{
3𝑥 − 𝑦 + 𝑧 = 2
𝑥 − 2𝑦 − 𝑧 = 0
2𝑥 + 𝑦 + 2𝑧 = 2
1º equação → 3.(-1) – (-2) + 3 = -3 + 2 + 3 = 2 (V)
2º equação → -1 -2.(-2) – 3 = -1 + 4 – 3 = 0 (V)
3º equação → 2.(-1) + (-2) + 2.3 = -2 – 2 + 6 = 2 (V)
Classificação de um sistema linear
Um sistema linear é classificado de acordo com seu números de soluções.
Exemplos:
A) O par ordenado (1,3) é a única solução do sistema {
2𝑥 − 𝑦 = −1
7𝑥 − 3𝑦 = −2
Temos que o sistema é possível e determinado (SPD)
B) O sistema {
3𝑥 − 3𝑦 + 3𝑧 = 3
𝑥 − 𝑦 + 𝑧 = 1
apresenta infinitas soluções, como por exemplo (0,1,2), (1,0,0),(2,-1,-
2). Dizemos que o sistema é possível e indeterminado (SPI)
C) O sistema {
𝑥 − 𝑦 + 𝑧 = 4
−4𝑥 + 2𝑦 − 𝑧 = 0
𝑥 − 𝑦 + 𝑧 = 2
não apresenta nenhuma solução, pois a primeira e a terceira
equações não podem satisfeitas ao mesmo tempo. Dizemos que o sistema é impossível (SI).
Sistemas escalonados
Considerando um sistema linear S no qual, em cada equação, existe pelo menos um coeficiente não
nulo.
Dizemos que S está na forma escalonada (ou é escalonado) se o número de coeficientes nulos, antes
do 1º coeficiente não nulo, aumenta de equação para equação.
Exemplos de sistemas escalonados:
Observe que o 1º sistema temos uma redução de números de coeficientes nulos: da 1ª para a 2ª
equação temos 1 e da 1ª para a 3ª temos 2; logo dizemos que ele é escalonado.
- Resolução de um sistema na forma escalonado
Temos dois tipos de sistemas escalonados.

175
1º) Número de equações igual ao número de variáveis
Vamos partir da última equação, onde obtemos o valor de z. Substituindo esse valor na segunda
equação obtemos y. Por fim, substituímos y e z na primeira equação, obtendo x.
Assim temos:
-2z = 8 → z = -4
y + z = -2 → y – 4 = -2 → y = 2
3x + 7y + 5z = -3 → 3x + 7.2 + 5.(-4) = -3 →3x + 14 – 20 = -3 →3x = -3 + 6 →3x = 3 → x = 1
Logo a solução para o sistema é (1,2,-4).
O sistema tem uma única solução logo é SPD.
2º) Número de equações menor que o número de variáveis.
{
𝑥 − 𝑦 + 3𝑧 = 5
𝑦 + 𝑧 = 2
Sabemos que não é possível determinar x,y e z de maneira única, pois há três variáveis e apenas duas
“informações” sobre as mesmas. A solução se dará em função de uma de suas variáveis, que será
chamada de variável livre do sistema.
Vamos ao passo a passo:
1º passo → a variável que não aparecer no início de nenhuma das equações do sistema será
convencionada como variável livre, neste caso, a única variável livre é z.
2º passo → transpomos a variável livre z para o 2º membro em cada equação e obtemos:
{
𝑥 − 𝑦 = 5 − 3𝑧
𝑦 = 2 − 𝑧
3º passo → para obtermos x como função de z, substituímos y = 2 – z, na equação:
x - (2 – z) = 5 – 3z → x = 7 – 4z
Assim, toda tripla ordenada da forma (7 – 4z, 2 – z, z), sendo z ϵ R, é solução do sistema. Para cada
valor real que atribuirmos a z, chegaremos a uma solução do sistema.
Este tipo de sistema é dado por infinitas soluções, por isso chamamos de SPI.
Sistemas equivalentes e escalonamento
Dizemos que dois sistemas lineares, S1 e S2, são equivalentes quando a solução de S1 também é
solução de S2.
Dado um sistema linear qualquer, nosso objetivo é transforma-lo em outro equivalente, pois como
vimos é fácil resolver um sistema de forma escalonada. Para isso, vamos aprender duas propriedades
que nos permitirá construir sistemas equivalentes.
1ª Propriedade: quando multiplicamos por k, k ϵ R*, os membros de
uma equação qualquer de um sistema linear S, obtemos um novo
sistema S’ equivalente a S.
𝑆 {
𝑥 − 𝑦 = 4
2𝑥 + 3𝑦 = 3
, 𝑐𝑢𝑗𝑎 𝑠𝑜𝑙𝑢çã𝑜 é (3, −1)
Multiplicando-se a 1ª equação de S por 3, por exemplo, obtemos:

176
𝑆′ {
3𝑥 − 3𝑦 = 12
6𝑥 + 9𝑦 = 9
, 𝑎 𝑠𝑜𝑙𝑢çã𝑜 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑎 𝑠𝑒𝑛𝑑𝑜 (3, −1)
2ª Propriedade: quando substituímos uma equação de um sistema
linear S pela soma, membro a membro, dele com outra, obtemos um
novo sistema S’, equivalente a S.
𝑆 {
−𝑥 + 𝑦 = −2
2𝑥 − 3𝑦 = 1
, 𝑐𝑢𝑗𝑎 𝑠𝑜𝑙𝑢çã𝑜 é (5,3)
Substituindo a 2ª equação pela soma dela com a 1ª:
𝑆′ {
−𝑥 + 𝑦 = −2
2𝑥 − 3𝑦 = 1
(2ª 𝑒𝑞.)+(1ª 𝑒𝑞.)
←
−𝑥 + 𝑦 = −2
2𝑥 − 3𝑦 = 1
𝑥 − 2𝑦 = −1
(+)
O par (5,3) é também solução de S’, pois a segunda também é
verificada:
x – 2y = 5 – 2. 3 = 5 – 6 = -1
Escalonamento de um sistema e o Método de Gauss-Jordan
Para escalonarmos um sistema linear qualquer vamos seguir o passo a passo abaixo:
1º passo: Escolhemos, para 1º equação, uma em que o coeficiente da 1ª incógnita seja não nulo. Se
possível, fazemos a escolha a fim de que esse coeficiente seja igual a -1 ou 1, pois os cálculos ficam, em
geral, mais simples.
2º passo: Anulamos o coeficiente da 1ª equação das demais equações, usando as propriedades 1 e
2.
3º passo: Desprezamos a 1ª equação e aplicamos os 2 primeiros passos com as equações restantes.
4º passo: Desprezamos a 1ª e a 2ª equações e aplicamos os dois primeiros passos nas equações,
até o sistema ficar escalonado.
Vejamos um exemplo:
Escalone e resolva o sistema:
{
−𝑥 + 𝑦 − 2𝑧 = −9
2𝑥 + 𝑦 + 𝑧 = 6
−2𝑥 − 2𝑦 + 𝑧 = 1
Primeiramente precisamos anular os coeficientes de x na 2ª e na 3ª equação:
Deixando de lado a 1ª equação, vamos repetir o processo para a 2ª e a 3ª equação. Convém,
entretanto, dividir os coeficientes da 2ª equação por 3, a fim de facilitar o escalonamento:
{
−𝑥 + 𝑦 − 2𝑧 = −9
𝑦 − 𝑧 = −4
−4𝑦 + 5𝑧 = 19

177
Que é equivalente a:
{
−𝑥 + 𝑦 − 2𝑧 = −9
𝑦 − 𝑧 = −4
𝑧 = 3
Substituímos a 3ª equação pela soma
dela com a 2ª equação, multiplicada por 4:
4𝑦−4𝑧=−16
−4𝑦+5𝑧=19
𝑧 = 3
O sistema obtido está escalonado é do tipo SPD.
A solução encontrada para o mesmo é (2,-1,3)
Observação: Quando, durante o escalonamento, encontramos duas equações com coeficientes
ordenadamente iguais ou proporcionais, podemos retirar uma delas do sistema.
Exemplo:
Escalone e resolva o sistema:
{
3𝑥 − 2𝑦 − 𝑧 = 0
𝑥 − 𝑦 + 2𝑧 = 1
8𝑥 − 6𝑦 + 2𝑧 = 2
{
𝑥 − 𝑦 + 2𝑧 = 1
3𝑥 − 2𝑦 − 𝑧 = 0
8𝑥 − 6𝑦 + 2𝑧 = 2
{
𝑥 − 𝑦 + 2𝑧 = 1
𝑦 − 7𝑧 = −3
2𝑦 − 14𝑧 = −6
(-3) x (1ª eq.) + (2ª eq.):
-3x + 3y – 6z = -3
3x – 2y – z = 0
y – 7z = -3
(-8) x (1eq.) + (3ª eq.)
-8x + 8y – 16z = -8
8x - 6y + 2z = 2
2y – 14z = -6
Deixamos a 1ª equação de lado e repetimos o processo para a 2ª e 3ª equação:
{
𝑥 − 𝑦 + 2𝑧 = 1
𝑦 − 7𝑧 = −3
0 = 0
(-2) x (2ª eq.) + (3ª eq.)
-2y + 14z = 6
2y – 14z = -6
0 = 0
A 3ª equação pode ser retirada do sistema, pois, apesar de ser sempre verdadeira, não traz informação
sobre os valores das variáveis. Assim, obtemos os sistema escalonado:
{
𝑥 − 𝑦 + 2𝑧 = 1 (𝐼)
𝑦 − 7𝑧 = −3 (𝐼𝐼)
, 𝑞𝑢𝑒 é 𝑑𝑜 𝑡𝑖𝑝𝑜 𝑆𝑃𝐼.
A variável livre do sistema é z, então temos:
(I) y = 7z – 3
(II) x – (7z – 3) + 2z = 1 → x = 5z – 2
Assim, S = [(5z – 2, 7z – 3, z); z ϵ R]

178
Sistemas homogêneos
Observe as equações lineares seguintes:
x – y + 2z = 0 4x – 2y + 5z = 0 -x1 – x2 – x3 = 0
O coeficiente independente de cada uma delas é igual a zero, então denominamos de equações
homogêneas.
Note que a tripla ordenada (0,0,0) é uma possível solução dessas equações, na qual chamamos de
solução nula, trivial ou imprópria.
Ao conjunto de equações homogêneas denominamos de sistemas homogêneos. Este tipo de sistema
é sempre possível, pois a solução nula satisfaz cada uma de suas equações.
Exemplo:
Escalonando o sistema {
𝑥 + 𝑦 − 𝑧 = 0
2𝑥 + 3𝑦 + 𝑧 = 0
5𝑥 + 7𝑦 + 𝑧 = 0
, 𝑣𝑒𝑚:
{
𝑥 + 𝑦 − 𝑧 = 0
𝑦 + 3𝑧 = 0 ← (−2)𝑥(1ª 𝑒𝑞. ) + (2ª 𝑒𝑞. )
2𝑦 + 6𝑧 = 0 ← (−5)𝑥(1ª 𝑒𝑞. ) + (3ª 𝑒𝑞. )
Dividindo os coeficientes da 3ª equação por 2, notamos que ela ficará igual à 2ª equação e, portanto
poderá ser retirada do sistema.
Assim, o sistema se reduz à forma escalonada {
𝑥 + 𝑦 − 𝑧 = 0
𝑦 + 3𝑧 = 0
𝑒 é 𝑑𝑜 𝑡𝑖𝑝𝑜 𝑆𝑃𝐼.
Resolvendo-o teremos y = -3z e x = 4z. Se z = α, α ϵ R, segue a solução geral (4α,-3α, α).
Vamos ver algumas de suas soluções:
- α = 0 → (0,0,0): solução nula ou trivial.
- α = 1 → (4,-3,1)
- α = -2 → (-8,6,-2)
As soluções onde α = 1 e – 2 são próprias ou diferentes da trivial.
Regra de Cramer
Consideramos o sistema {
𝑎𝑥 + 𝑏𝑦 = 𝑒
𝑐𝑥 + 𝑑𝑦 = 𝑓
. Suponhamos que a ≠ 0. Observamos que a matriz incompleta
desse sistema é 𝑀 = (
𝑎 𝑏
𝑐 𝑑
), cujo determinante é indicado por D = ad – bc.
Escalonando o sistema, obtemos: {
(𝑎𝑑 − 𝑏𝑐). 𝑦 = (𝑎𝑓 − 𝑐𝑒)
(∗)
Se substituirmos em M a 2ª coluna (dos coeficientes de y) pela coluna dos coeficientes independentes,
obteremos (
𝑎 𝑒
𝑐 𝑓), cujo determinante é indicado por Dy = af – ce.
Assim, em (*), na 2ª equação, obtemos D. y = Dy. Se D ≠ 0, segue que 𝑦 =
𝐷𝑦
𝐷
.

179
Substituindo esse valor de y na 1ª equação de (*) e considerando a matriz (
𝑒 𝑏
𝑓 𝑑
), cujo determinante
é indicado por Dx = ed – bf, obtemos 𝑥 =
𝐷𝑥
𝐷
, D ≠ 0.
Resumindo:
Um sistema {
é possível e determinado quando 𝐷 = |
𝑎 𝑏
𝑐 𝑑
| ≠ 0, e a solução desse sistema
é dada por:
𝒙 =
𝑫𝒙
𝑫
𝒆 𝒚 =
𝑫𝒚
𝑫
Estes resultados são conhecidos como Regra de Cramer e podem ser generalizados para um sistema
n x n (n equações e n incógnitas). Esta regra é um importante recurso na resolução de sistemas lineares
possíveis e determinados, especialmente quando o escalonamento se torna trabalhoso (por causa dos
coeficientes das equações) ou quando o sistema é literal.
Exemplo:
Vamos aplicar a Regra de Cramer para resolver os sistema {
𝑥 + 𝑦 + 𝑧 = 0
4𝑥 − 𝑦 − 5𝑧 = −6
2𝑥 + 𝑦 + 2𝑧 = −3
De início temos que |
1 1 1
4 −1 −5
2 1 2
| = −9 ≠ 0. Temos, dessa forma, SPD.
𝐷𝑥 = |
0 1 1
−6 −1 −5
−3 1 2
| = 15 − 6 − 3 + 12 = 18; 𝑥 =
𝐷𝑥
𝐷
=
18
−9
= −2
𝐷𝑦 = |
1 0 1
4 −6 −5
2 −3 2
| = −12 − 12 + 12 − 15 = −27;𝑦 =
𝐷𝑦
𝐷
=
−27
−9
= 3
𝐷𝑧 = |
1 1 0
4 −1 −6
2 1 −3
| = 3 − 12 + 6 + 12 = 9; 𝑧 =
𝐷𝑧
𝐷
=
9
−9
= −1
Uma alternativa para encontrar o valor de z seria substituir x por -2 e y por 3 em qualquer uma das
equações do sistema.
Assim, S = {(-2,3-1)}.
Discussão de um sistema
Consideremos novamente o sistema {
, cuja forma escalonada é:
{
(𝑎𝑑 − 𝑏𝑐)
⏟
𝐷
. 𝑦 = (𝑎𝑓 − 𝑐𝑒)(∗)
em que 𝐷 = |
𝑎 𝑏
𝑐 𝑑
| é o determinante da matriz incompleta do sistema.
Como vimos, se D ≠ 0, o sistema é possível e determinado e a solução pode ser obtida através da
Regra de Cramer.
Se D = 0, o 1º membro de (*) se anula. Dependendo do anulamento, ou não, do 2º membro de (*),
temos SPI ou SI.
Em geral, sendo D o determinante da matriz incompleta dos coeficientes de um sistema linear, temos:

180
D ≠ 0 → SPD
D = 0 → (SPI ou SI)
Esses resultados são válidos para qualquer sistema linear de n equações e n incógnitas, n ≥ 2. Temos
que discutir um sistema linear em função de um ou mais parâmetros significa dizer quais valores do(s)
parâmetro(s) temos SPD, SPI ou SI.
Exemplo:
Vamos discutir, em função de m, o sistema {
𝑥 − 2𝑦 + 3𝑧 = 0
3𝑥 + 𝑦 + 𝑧 = 2
2𝑥 + 3𝑦 + 𝑚𝑧 = 2
Temos: 𝐷 = |
1 −2 3
3 1 1
2 3 𝑚
| = 𝑚 − 4 + 27 − 6 − 3 + 6𝑚 − 7𝑚 + 14
- Se 7m + 14 ≠ 0, isto é, se m ≠ - 2, temos SPD.
- Se 7m + 14 = 0, isto é, se m = -2, podemos ter SI ou SPI. Então vamos substituir m por -2 no sistema
e resolvê-lo:
{
𝑥 − 2𝑦 + 3𝑧 = 0
3𝑥 + 𝑦 + 𝑧 = 2
2𝑥 + 3𝑦 − 2𝑧 = 2
⟺ {
𝑥 − 2𝑦 + 3𝑧 = 0
7𝑦 − 8𝑧 = 2 ⟵ (−3)𝑥 (1ª 𝑒𝑞. ) + (2ª 𝑒𝑞. )
7𝑦 − 8𝑧 = 2 ⟵ (−2)𝑥 (1ª 𝑒𝑞. ) + (3ª 𝑒𝑞. )
ou ainda {
𝑥 − 2𝑦 + 3𝑧 = 0
7𝑦 − 8𝑧 = 2
, 𝑞𝑢𝑒 é 𝑒𝑠𝑐𝑎𝑙𝑜𝑛𝑎𝑑𝑜 𝑒 𝑑𝑜 𝑡𝑖𝑝𝑜 𝑆𝑃𝐼.
Assim:
m ≠ - 2 → SPD
m = -2 → SPI
Observações:
- Para um sistema homogêneo, a condição D = 0, é necessária para que tenhamos SPI, mas não é
suficiente (pois existe a possibilidade de se ter SI).
- Para um sistema homogêneo, a condição D = 0 é suficiente para que tenhamos SPI.
Questões
01. (MF – Analista de Finanças e Controle – ESAEF) Dado o sistema de equações lineares
é correto afirmar que:
(A) o sistema não possui solução.
(B) o sistema possui uma única solução.
(C) x= 1 e y = 2 é uma solução do sistema.
(D) o sistema é homogêneo.
(E) o sistema possui mais de uma solução.
02. Determinar m real, para que o sistema seja possível e determinado:







2
5
3
2
my
x
y
x
03. Resolver e classificar o sistema:














4
2
2
7
3
5
3
z
y
x
y
x
z
y
x

181
04. Determinar m real para que o sistema seja possível e determinado.














0
3
5
2
2
5
2
mz
y
x
z
y
x
z
y
x
05. Se o terno ordenado (2, 5, p) é solução da equação linear 6x - 7y + 2z = 5, qual o valor de p?
06. Escreva a solução genérica para a equação linear 5x - 2y + z = 14, sabendo que o terno ordenado
(𝛼, 𝛽, 𝛾) é solução.
07. Determine o valor de m de modo que o sistema de equações abaixo,
2x - my = 10
3x + 5y = 8, seja impossível.
08. Se os sistemas:
S1: {
x + y = 1
x – 2y = −5
e S2: {
ax – by = 5
ay – bx = −1
São equivalentes, então o valor de a2
+ b2
é igual a:
(A) 1
(B) 4
(C) 5
(D) 9
(E) 10
09. Resolva o seguinte sistema usando a regra de Cramer:
{
x + 3y − 2z = 3
2x − y + z = 12
4x + 3y − 5z = 6
10. Resolver o sistema








2
5
7
2
y
x
y
x
.
11. (UNIOESTE – ANALISTA DE INFORMÁTICA – UNIOESTE) Considere o seguinte sistema de
equações lineares
(
𝑥 + 2𝑦 +
3
2 𝑧 =
3
2
2𝑥 + 𝑦 + 𝑧 = 2
2𝑥 + 4𝑦 + 3𝑧 = 3
)
Assinale a alternativa correta.
(A) O determinante da matriz dos coeficientes do sistema é um número estritamente positivo.
(B) O sistema possui uma única solução (1, 1, -1).
(C) O sistema possui infinitas soluções.
(D) O posto da matriz ampliada associada ao sistema é igual a 3.
(E) Os vetores linha (1, 2, 3/2) e (2, 4, 3) não são colineares.
12. (SEDUC/RJ - Professor – Matemática – CEPERJ) Sabendo-se que 2a + 3b + 4c = 17 e que 4a +
b - 2c = 9, o valor de a + b + c é:
(A) 3.
(B) 4.
(C) 5.
(D) 6.
(E) 7.
Comentários

182
01. Resposta: E.
Calculemos inicialmente D, Dx e Dy:
0
12
12
6
3
4
2




D
0
36
36
6
9
4
6




x
D
0
18
18
9
3
6
2




y
D
Como D = Dx = Dy = 0, o sistema é possível e indeterminado, logo possui mais de uma solução.
02. Resposta:








2
3
/m
R
m .
Segundo a regra de Cramer, devemos ter D ≠ 0, em que:
3
2
1
3
2


 m
m
D
Assim: 2m -3 ≠ 0 → m ≠
2
3
Então, os valores reais de m, para que o sistema seja possível e determinado, são dados pelos
elementos do conjunto:








2
3
/m
R
m
03. Resposta: S = {(1, 2, 4)}.
Calculemos inicialmente D, Dx, Dy e Dz

183
Como D= -25 ≠ 0, o sistema é possível e determinado e:
;
1
25
25





D
D
x x ;
2
25
50





D
D
y
y
4
25
100




D
D
z z
Assim: S = {(1, 2, 4)} e o sistema são possíveis e determinados.
04. Resposta:  
3
/ 
 m
R
m .
Segundo a regra de Cramer, devemos ter D ≠ 0.
Assim:
m
m
m
D 4
2
3
2
12
1
3
2
1
2
1
2
1









D = -5m + 15
Assim: -5m + 15 ≠ 0 → m ≠ 3
Então, os valores reais de m, para que o sistema seja possível e determinado, são dados pelos
elementos do conjunto:
 
3
/ 
 m
R
m
05. Resposta: 14.
Teremos por simples substituição, observando que x = 2, y = 5 e z = p, 6 . 2 – 7 . 5 + 2 . p = 5.
Logo, 12 - 35 + 2p = 5.
Daí vem imediatamente que 2p = 28 e, portanto, p = 14.
06. Resposta: S = (1,3,15).
Podemos escrever: 5α - 2β + γ = 14. Daí, tiramos: γ = 14 - 5α + 2β. Portanto, a solução genérica será
o terno ordenado (α, β, 14 - 5α + 2β).
Observe que se arbitrando os valores para α e β, a terceira variável ficará determinada em função
desses valores.
Por exemplo, fazendo-se α = 1, β = 3, teremos:
γ = 14 - 5 α + 2 β = 14 – 5 . 1 + 2 . 3 = 15,
ou seja, o terno (1, 3, 15) é solução, e assim, sucessivamente.
Verificamos, pois que existem infinitas soluções para a equação linear dada, sendo o terno
ordenado (α, β, 14 - 5 α + 2 β) a solução genérica.
07. Resposta: m = -10/3.
Teremos, expressando x em função de m, na primeira equação:
x = (10 + my) / 2
Substituindo o valor de x na segunda equação, vem:
3[(10+my) / 2] + 5y = 8
Multiplicando ambos os membros por 2, desenvolvendo e simplificando, vem:

184
3(10+my) + 10y = 16
30 + 3my + 10y = 16
(3m + 10)y = -14
y = -14 / (3m + 10)
Ora, para que não exista o valor de y e, em consequência não exista o valor de x, deveremos ter o
denominador igual a zero, já que, como sabemos, não existe divisão por zero.
Portanto, 3m + 10 = 0, de onde se conclui m = -10/3, para que o sistema seja impossível, ou seja, não
possua solução.
08. Resposta: E.
Como os sistemas são equivalentes, eles possuem a mesma solução. Vamos resolver o sistema:
S1: x + y = 1
x - 2y = -5
Subtraindo membro a membro, vem: x - x + y - (-2y) = 1 - (-5).
Logo, 3y = 6 y = 2.
Portanto, como x + y = 1, vem, substituindo: x + 2 = 1 x = -1.
O conjunto solução é, portanto S = {(-1, 2)}.
Como os sistemas são equivalentes, a solução acima é também solução do sistema S2.
Logo, substituindo em S2 os valores de x e y encontrados para o sistema S1, vem:
a(-1) - b(2) = 5 → - a - 2b = 5
a(2) - b (-1) = -1 → 2 a + b = -1
Multiplicando ambos os membros da primeira equação por 2, fica:
-2 a - 4b = 10
Somando membro a membro esta equação obtida com a segunda equação, fica:
-3b = 9 b = - 3
Substituindo o valor encontrado para b na equação em vermelho acima (poderia ser também na outra
equação em azul), teremos:
2 a + (-3) = -1 a = 1.
Portanto, a2
+ b2
= 12
+ (-3)2
= 1 + 9 = 10.
09. Resposta: S = {(5, 2, 4)}.
Teremos:
Portanto, pela regra de Cramer, teremos:
x1 = D x1 / D = 120 / 24 = 5

185
x2 = D x2 / D = 48 / 24 = 2
x3 = D x3 / D = 96 / 24 = 4
Logo, o conjunto solução do sistema dado é S = {(5, 2, 4)}.
10. Resposta:  
 
1
3 
 ,
S
11. Resposta: C.
𝐷 = |
1 2
2 1
3
2
1
2 4 3
| = 3 + 12 + 4 − 3 − 4 − 12 = 0
O sistema pode ser SI (sistema impossível) ou SPI (sistema possível indeterminado)
Para ser SI Dx = 0 e SPI Dx  0
𝐷𝑥 = |
3
2
2
2 1
3
2
1
3 4 3
| =
9
2
+ 6 + 24 −
9
2
− 6 − 12 = 12
Dx  0, portanto o sistema tem infinitas soluções.
12. Reposta: D.
(I) 2a + 3b + 4c = 17 x(-2)
(II) 4a + b – 2c = 9
Multiplicamos a primeira equação por – 2 e somamos com a segunda, cancelando a variável a:
(I) 2a + 3b + 4c = 17
(II) – 5b – 10c = - 25 : (- 5)
Então:
(I) 2a + 3b + 4c = 17
(II) b +2c = 5
Um sistema com três variáveis e duas equações é possível e indeterminado (tem infinitas soluções),
então fazendo a variável c = α (qualquer letra grega).
Substituímos c em (II):
b + 2α = 5
b = 5 - 2α
substituímos b e c em (I):
2a + 3(5 - 2α) + 4α = 17
2a + 15 - 6α + 4α = 17
2a = 17 – 15 + 6α - 4α
2a = 2 + 2α : (2)
a = 1 + α
Logo a solução do sistema é a = 1 + α. b = 5 - 2α e c = α, então:
a + b + c = 1 + α + 5 - 2α + α = 6

186
SEQUÊNCIAS
Podemos, no nosso dia-a-dia, estabelecer diversas sequências como, por exemplo, a sucessão de
cidades que temos numa viagem de automóvel entre Brasília e São Paulo ou a sucessão das datas de
aniversário dos alunos de uma determinada escola.
Podemos, também, adotar para essas sequências uma ordem numérica, ou seja, adotando a1 para o
1º termo, a2 para o 2º termo até an para o n-ésimo termo. Dizemos que o termo an é também chamado
termo geral das sequências, em que n é um número natural diferente de zero. Evidentemente, daremos
atenção ao estudo das sequências numéricas.
As sequências podem ser finitas, quando apresentam um último termo, ou, infinitas, quando não
apresentam um último termo. As sequências infinitas são indicadas por reticências no final.
Exemplos:
- Sequência dos números primos positivos: (2, 3, 5, 7, 11, 13, 17, 19, ...). Notemos que esta é uma
sequência infinita com a1 = 2; a2 = 3; a3 = 5; a4 = 7; a5 = 11; a6 = 13 etc.
- Sequência dos números ímpares positivos: (1, 3, 5, 7, 9, 11, ...). Notemos que esta é uma sequência
infinita com a1 = 1; a2 = 3; a3 = 5; a4 = 7; a5 = 9; a6 = 11 etc.
- Sequência dos algarismos do sistema decimal de numeração: (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Notemos
que esta é uma sequência finita com a1 = 0; a2 = 1; a3 = 2; a4 = 3; a5 = 4; a6 = 5; a7 = 6; a8 = 7; a9 = 8; a10
= 9.
Igualdade de Sequências
As sequências são apresentadas com os seus termos entre parênteses colocados de forma ordenada.
Sucessões que apresentarem os mesmos termos em ordem diferente serão consideradas sucessões
diferentes.
Duas sequências só poderão ser consideradas iguais se, e somente se, apresentarem os mesmos
termos, na mesma ordem.
Exemplo
A sequência (x, y, z, t) poderá ser considerada igual à sequência (5, 8, 15, 17) se, e somente se, x =
5; y = 8; z = 15; e t = 17.
Notemos que as sequências (0, 1, 2, 3, 4, 5) e (5, 4, 3, 2, 1, 0) são diferentes, pois, embora apresentem
os mesmos elementos, eles estão em ordem diferente.
Termo Geral
Podemos apresentar uma sequência através de um determinado valor atribuído a cada termo an em
função do valor de n, ou seja, dependendo da posição do termo. Esta fórmula que determina o valor do
termo an é chamada fórmula do termo geral da sucessão.
Exemplos
Determinar os cincos primeiros termos da sequência cujo termo geral é igual a:
an = n2
– 2n, com n ∈ N*.
Teremos:
- se n = 1 ⇒ a1 = 12
– 2. 1 ⇒ a1 = 1 – 2 = - 1
- se n = 2 ⇒ a2 = 22
– 2. 2 ⇒ a2 = 4 – 4 = 0
- se n = 3 ⇒ a3 = 32
– 2. 3 ⇒ a3 = 9 – 6 = 3
- se n = 4 ⇒ a4 = 42
– 4. 2 ⇒ a4 =16 – 8 = 8
- se n = 5 ⇒ a5 = 52
– 5. 2 ⇒ a5 = 25 – 10 = 15
Determinar os cinco primeiros termos da sequência cujo termo geral é igual a:
an = 3n + 2, com n ∈ N*.
10 - Sequências. 11 - Progressões aritméticas e progressões geométricas.

187
- se n = 1 ⇒ a1 = 3.1 + 2 ⇒ a1 = 3 + 2 = 5
- se n = 2 ⇒ a2 = 3.2 + 2 ⇒ a2 = 6 + 2 = 8
- se n = 3 ⇒ a3 = 3.3 + 2 ⇒ a3 = 9 + 2 = 11
- se n = 4 ⇒ a4 = 3.4 + 2 ⇒ a4 = 12 + 2 = 14
- se n = 5 ⇒ a5 = 3.5 + 2 ⇒ a5 = 15 + 2 = 17
Determinar os termos a12 e a23 da sequência cujo termo geral é igual a:
an = 45 – 4n, com n ∈ N*.
Teremos:
- se n = 12 ⇒ a12 = 45 – 4.12 ⇒ a12 = 45 – 48 = - 3
- se n = 23 ⇒ a23 = 45 – 4.23 ⇒ a23 = 45 – 92 = - 47
Lei de Recorrências
Uma sequência pode ser definida quando oferecemos o valor do primeiro termo e um “caminho” (uma
fórmula) que permite a determinação de cada termo conhecendo-se o seu antecedente. Essa forma de
apresentação de uma sucessão é chamada lei de recorrências.
Exemplos
Escrever os cinco primeiros termos de uma sequência em que:
a1 = 3 e an+1 = 2an – 4, em que n ∈ N*.
Teremos: o primeiro termo já foi dado.
- a1 = 3
- se n = 1 ⇒ a1+1 = 2.a1 – 4 ⇒ a2 = 2.3 – 4 ⇒ a2 = 6 – 4 = 2
- se n = 2 ⇒ a2+1 = 2.a2 – 4 ⇒ a3 = 2.2 – 4 ⇒ a3 = 4 – 4 = 0
- se n = 3 ⇒ a3+1 = 2.a3 – 4 ⇒ a4 = 2.0 – 4 ⇒ a4 = 0 – 4 = - 4
- se n = 4 ⇒ a4+1 = 2.a4 – 4 ⇒ a5 = 2.(-4) – 4 ⇒ a5 = - 8 – 4 = - 12
Determinar o termo a5 de uma sequência em que:
a1 = 12 e an+ 1 = an – 2, em que n ∈ N*.
- a1 = 12
- se n = 1 ⇒ a1+1 = a1 – 2 ⇒ a2 = 12 – 2 ⇒ a2=10
- se n = 2 ⇒ a2+1 = a2 – 2 ⇒ a3 = 10 – 2 ⇒ a3 = 8
- se n = 3 ⇒ a3+1 = a3 – 2 ⇒ a4 = 8 – 2 ⇒ a4 = 6
- se n = 4 ⇒ a4+1 = a4 – 2 ⇒ a5 = 6 – 2 ⇒ a5 = 4
Observação 1
Devemos observar que a apresentação de uma sequência através do termo geral é mais pratica, visto
que podemos determinar um termo no “meio” da sequência sem a necessidade de determinarmos os
termos intermediários, como ocorre na apresentação da sequência através da lei de recorrências.
Observação 2
Algumas sequências não podem, pela sua forma “desorganizada” de se apresentarem, ser definidas
nem pela lei das recorrências, nem pela fórmula do termo geral. Um exemplo de uma sequência como
esta é a sucessão de números naturais primos que já “destruiu” todas as tentativas de se encontrar uma
fórmula geral para seus termos.
Observação 3
Em todo exercício de sequência em que n ∈ N*
, o primeiro valor adotado é n = 1. No entanto de no
enunciado estiver n > 3, temos que o primeiro valor adotado é n = 4. Lembrando que n é sempre um
número natural.
A Matemática estuda dois tipos especiais de sequências, uma delas a Progressão Aritmética.

188
Sequência de Fibonacci
O matemático Leonardo Pisa, conhecido como Fibonacci, propôs no século XIII, a sequência numérica:
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …). Essa sequência tem uma lei de formação simples: cada elemento,
a partir do terceiro, é obtido somando-se os dois anteriores. Veja: 1 + 1 = 2, 2 + 1 = 3, 3 + 2 = 5 e assim
por diante. Desde o século XIII, muitos matemáticos, além do próprio Fibonacci, dedicaram-se ao estudo
da sequência que foi proposta, e foram encontradas inúmeras aplicações para ela no desenvolvimento
de modelos explicativos de fenômenos naturais.
Veja alguns exemplos das aplicações da sequência de Fibonacci e entenda porque ela é conhecida
como uma das maravilhas da Matemática. A partir de dois quadrados de lado 1, podemos obter um
retângulo de lados 2 e 1. Se adicionarmos a esse retângulo um quadrado de lado 2, obtemos um novo
retângulo 3 x 2. Se adicionarmos agora um quadrado de lado 3, obtemos um retângulo 5 x 3. Observe a
figura a seguir e veja que os lados dos quadrados que adicionamos para determinar os retângulos formam
a sequência de Fibonacci.
Se utilizarmos um compasso e traçarmos o quarto de circunferência inscrito em cada quadrado,
encontraremos uma espiral formada pela concordância de arcos cujos raios são os elementos da
sequência de Fibonacci.
O Partenon que foi construído em Atenas pelo célebre arquiteto grego Fidias. A fachada principal do
edifício, hoje em ruínas, era um retângulo que continha um quadrado de lado igual à altura. Essa forma
sempre foi considerada satisfatória do ponto de vista estético por suas proporções sendo chamada
retângulo áureo ou retângulo de ouro.
Como os dois retângulos indicados na figura são semelhantes temos:
𝑦
𝑎
=
𝑎
𝑏
(1).

189
Como: b = y – a (2).
Substituindo (2) em (1) temos: y2
– ay – a2
= 0.
Resolvendo a equação:
𝑦 =
𝑎(1±√5
2
em que (
1−√5
2
< 0) não convém.
Logo:
𝑦
𝑎
=
(1+√5
2
= 1,61803398875
Esse número é conhecido como número de ouro e pode ser representado por:
𝜃 =
1 + √5
2
Todo retângulo e que a razão entre o maior e o menor lado for igual a 𝜃 é chamado retângulo áureo
como o caso da fachada do Partenon.
PROGRESSÃO ARITMÉTICA (P.A.)
Definição
É uma sequência numérica em que cada termo, a partir do segundo, é igual ao termo anterior somado
com uma constante que é chamada de razão (r).
Como em qualquer sequência os termos são chamados de a1, a2, a3, a4, ......., an, ....
Cálculo da razão
A razão de uma Progressão Aritmética é dada pela diferença de um termo qualquer pelo termo
imediatamente anterior a ele.
r = a2 – a1 = a3 – a2 = a4 – a3 = a5 – a4 = .......... = an – an – 1
Exemplos:
- (5, 9, 13, 17, 21, 25, ......) é uma P.A. onde a1 = 5 e razão r = 4
- (2, 9, 16, 23, 30, …) é uma P.A. onde a1 = 2 e razão r = 7
- (23, 21, 19, 17, 15, …) é uma P.A. onde a1 = 23 e razão r = - 2.
Classificação
Uma P.A. é classificada de acordo com a razão.
1- Se r > 0 ⇒ a P.A. é crescente.
2- Se r < 0 ⇒ a P.A. é decrescente.
3- Se r = 0 ⇒ a P.A. é constante.
Fórmula do Termo Geral
Em toda P.A., cada termo é o anterior somado com a razão, então temos:
1° termo: a1
2° termo: a2 = a1 + r
3° termo: a3 = a2 + r = a1 + r + r = a1 + 2r
4° termo: a4 = a3 + r = a1 + 2r + r = a1 + 3r
5° termo: a5 = a4 + r = a1 + 3r + r = a1 + 4r
6° termo: a6 = a5 + r = a1 + 4r + r = a1 + 5r
. . . . . .
. . . . . .
. . . . . .
n° termo é:

190
Fórmula da soma dos n primeiros termos
Propriedades
1- Numa P.A. a soma dos termos equidistantes dos extremos é igual à soma dos extremos.
Exemplos
01. (1, 3, 5, 7, 9, 11, ......)
02. (2, 8, 14, 20, 26, 32, 38, ......)
Como podemos observar neste exemplo, temos um número ímpar de termos. Neste caso sobrou um
termo no meio (20) que é chamado de termo médio e é igual a metade da soma dos extremos. Porém,
só existe termos médios se houver um número ímpar de termos.
2- Numa P.A. se tivermos três termos consecutivos, o termo médio é igual à média aritmética dos
anterior com o posterior. Ou seja, (a1, a2, a3, ...)
a2 =
a3
a1
.
Exemplo
P.G. – PROGRESSÃO GEOMÉTRICA
Definição
É uma sequência numérica em que cada termo, a partir do segundo termo, é igual ao termo anterior
multiplicado por uma constante que é chamada de razão (q).
Como em qualquer sequência os termos são chamados de a1, a2, a3, a4, ......., an,...
Cálculo da razão
A razão de uma Progressão Geométrica é dada pelo quociente de um termo qualquer pelo termo
imediatamente anterior a ele.
𝑞 =
𝑎2
𝑎1
=
𝑎3
𝑎2
=
𝑎4
𝑎3
= ⋯ … … … =
𝑎𝑛
𝑎𝑛−1
Exemplos
- (3, 6, 12, 24, 48, ...) é uma PG de primeiro termo a1 = 3 e razão q = 2
- (-36, -18, -9,
−9
2
,
−9
4
,...) é uma PG de primeiro termo a1 = - 36 e razão q =
1
2
- (15, 5,
5
3
,
5
9
,...) é uma PG de primeiro termo a1 = 15 e razão q =
1
3
- (- 2, - 6, -18, - 54, ...) é uma PG de primeiro termo a1 = - 2 e razão q = 3
- (1, - 3, 9, - 27, 81, - 243, ...) é uma PG de primeiro termo a1 = 1 e razão q = - 3
- (5, 5, 5, 5, 5, 5, ...) é uma PG de primeiro termo a1 = 5 e razão q = 1
- (7, 0, 0, 0, 0, 0, ...) é uma PG de primeiro termo a1 = 7 e razão q = 0
- (0, 0, 0, 0, 0, 0, ...) é uma PG de primeiro termo a1 = 0 e razão q indeterminada

191
Classificação
Uma P.G. é classificada de acordo com o primeiro termo e a razão.
1- Crescente: quando cada termo é maior que o anterior. Isto ocorre quando a1 > 0 e q > 1 ou quando
a1 < 0 e 0 < q < 1.
2- Decrescente: quando cada termo é menor que o anterior. Isto ocorre quando a1 > 0 e 0 < q < 1 ou
quando a1 < 0 e q > 1.
3- Alternante: quando cada termo apresenta sinal contrário ao do anterior. Isto ocorre quando q < 0.
4- Constante: quando todos os termos são iguais. Isto ocorre quando q = 1. Uma PG constante é
também uma PA de razão r = 0. A PG constante é também chamada de PG estacionária.
5- Singular: quando zero é um dos seus termos. Isto ocorre quando a1 = 0 ou q = 0.
Fórmula do Termo Geral
Em toda P.G. cada termo é o anterior multiplicado pela razão, então temos:
1° termo: a1
2° termo: a2 = a1.q
3° termo: a3 = a2.q = a1.q.q = a1q2
4° termo: a4 = a3.q = a1.q2
.q = a1.q3
5° termo: a5 = a4.q = a1.q3
.q = a1.q4
. . . . .
. . . . .
. . . . .
n° termo é:
Soma dos n primeiros termos (Soma Finita)
Soma dos infinitos termos (ou Limite da soma)
Vamos ver um exemplo:
Seja a P.G. (2, 1, ½, ¼, 1/8, 1/16, 1/32, …) de a1 = 2 e q =
1
2
se colocarmos na forma decimal, temos
(2; 1; 0,5; 0,25; 0,125; 0,0625; 0,03125; ….) se efetuarmos a somas destes termos:
2 + 1 = 3
3 + 0,5 = 3,5
3,5 + 0,25 = 3,75
3,75 + 0,125 = 3,875
3,875 + 0,0625 = 3,9375
3,9375 + 0,03125 = 3,96875
.
.
.
Como podemos observar o número somado vai ficando cada vez menor e a soma tende a um certo
limite. Então temos a seguinte fórmula:
Utilizando no exemplo acima: 𝑆 =
2
1−
1
2
=
2
1
2
= 4, logo dizemos que esta P.G. tem um limite que tenda a
4.

192
Produto da soma de n termos
Temos as seguintes regras para o produto, já que esta fórmula está em módulo:
1- O produto de n números positivos é sempre positivo.
2- No produto de n números negativos:
a) se n é par: o produto é positivo.
b) se n é ímpar: o produto é negativo.
Propriedades
1- Numa P.G., com n termos, o produto de dois termos equidistantes dos extremos é igual ao produto
destes extremos.
Exemplos
01. (3, 6, 12, 24, 48, 96, 192, 384, ...)
02. (1, 2, 4, 8, 16, 32, 64, …)
Como podemos observar, temos um número ímpar de termos. Neste caso sobrou um termo no meio
(8) que é chamado de termo médio e é igual a raiz quadrada do produto dos extremos. Porém, só
existe termo médio se houver um número ímpar de termos.
2- Numa P.G. se tivermos três termos consecutivos, o termo médio é igual à média geométrica do
termo anterior com o termo posterior. Ou seja, (a1, a2, a3, ...) <==> a2 = √a3. a1.
Exemplo
Questões
01. (Câm. Municipal de Eldorado do Sul/RS – Técnico Legislativo – FUNDATEC/2018) Para
organizar a rotina de trabalho, um técnico legislativo protocola os processos diariamente, de acordo com
as demandas. Supondo que o número de processos aumenta diariamente em progressão aritmética e
que no primeiro dia foram protocolados cinco processos e 33 no décimo quinto dia, quantos processos
serão protocolados no trigésimo dia?
(A) 20.
(B) 35.
(C) 48.
(D) 63.
(E) 66.

193
02. (FUB – Assistente em Administração – CESPE/2018) A tabela seguinte mostra as quantidades
de livros de uma biblioteca que foram emprestados em cada um dos seis primeiros meses de 2017.
A partir dessa tabela, julgue o próximo item.
Situação hipotética: Os livros emprestados no referido semestre foram devolvidos somente a partir de
julho de 2017 e os números correspondentes às quantidades de livros devolvidos a cada mês formavam
uma progressão aritmética em que o primeiro termo era 90 e razão, 30. Assertiva: Nessa situação, mais
de 200 livros foram devolvidos somente a partir de 2018.
( ) Certo ( ) Errado
03. (SEFAZ/RS – Assistente Administrativo Fazendário – CESPE/2018) Sobre uma mesa há 9
caixas vazias. Em uma dessas caixas, será colocado um grão de feijão; depois, em outra caixa, serão
colocados três grãos de feijão. Prosseguindo-se sucessivamente, será escolhida uma caixa vazia, e nela
colocada uma quantidade de grãos de feijão igual ao triplo da quantidade colocada na caixa anteriormente
escolhida, até que não reste caixa vazia.
Nessa situação, nas 9 caixas será colocada uma quantidade de grãos de feijão igual a
(A)
39−1
2
(B) 39
− 1
(C)
310−1
2
(D) 310
− 1
(E)
38−3
2
04. (Pref. Amparo/SP – Agente Escolar – CONRIO) Descubra o 99º termo da P.A. (45, 48, 51, ...)
(A) 339
(B) 337
(C) 333
(D) 331
05. (Câm. de São Paulo/SP – Técnico Administrativo – FCC) Uma sequência inicia-se com o número
0,3. A partir do 2º termo, a regra de obtenção dos novos termos é o termo anterior menos 0,07. Dessa
maneira o número que corresponde à soma do 4º e do 7º termos dessa sequência é
(A) –6,7.
(B) 0,23.
(C) –3,1.
(D) –0,03.
(E) –0,23.
06. (EBSERH/UFSM/RS – Analista Administrativo – AOCP) Observe a sequência:
1; 2; 4; 8;...
Qual é a soma do sexto termo com o oitavo termo?
(A) 192
(B) 184
(C) 160
(D) 128
(E) 64
Se observar teremos uma PG de razão q = 2 e a1 = 1, portanto vamos encontrar o valor do a6 e do
a8, podemos fazer por fórmula e sem fórmula, pois os números são pequenos.
Fórmula do termo geral
𝑎𝑛 = 𝑎1. 𝑞𝑛−1
Assim:

194
𝑎6 = 1.26−1
= 25
= 32
𝑎8 = 1. 28−1
= 27
= 128
Se fosse sem fórmula basta ir multiplicando por 2 a soma e encontrar o sexto e oitavo termo: 1, 2, 4,
8, 16, 32, 64, 128
A soma fica: 32 + 128 = 160.
07. (Pref. Nepomuceno/MG – Técnico em Segurança do Trabalho – CONSULPLAN) O primeiro e
o terceiro termos de uma progressão geométrica crescente são, respectivamente, 4 e 100. A soma do
segundo e quarto termos dessa sequência é igual a
(A) 210.
(B) 250.
(C) 360.
(D) 480.
(E) 520.
08. (TRF/ 3ª Região – Analista Judiciário – FCC) Um tabuleiro de xadrez possui 64 casas. Se fosse
possível colocar 1 grão de arroz na primeira casa, 4 grãos na segunda, 16 grãos na terceira, 64 grãos na
quarta, 256 na quinta, e assim sucessivamente, o total de grãos de arroz que deveria ser colocado na 64ª
casa desse tabuleiro seria igual a
(A) 264
.
(B) 2126
.
(C) 266
.
(D) 2128
.
(E) 2256
.
09. (Polícia Militar/SP – Aluno Oficial – VUNESP) Planejando uma operação de policiamento
ostensivo, um oficial desenhou em um mapa três círculos concêntricos de centro P, conforme mostrado
na figura.
Sabe-se que as medidas dos raios r, r1 e r2 estão, nessa ordem, em progressão geométrica. Se r + r1
+ r2 = 52 cm, e r . r2 = 144 cm, então r + r2 é igual, em centímetros, a
(A) 36.
(B) 38.
(C) 39.
(D) 40.
(E) 42.
10. (EBSERH/UFGD – Técnico em Informática – AOCP) Observe a sequência numérica a seguir:
11; 15; 19; 23;...
Qual é o sétimo termo desta sequência?
(A) 27.
(B) 31.
(C) 35.
(D) 37.
(E) 39

195
11. (METRÔ/SP – Usinador Ferramenteiro – FCC) O setor de almoxarifado do Metrô necessita
numerar peças de 1 até 100 com adesivos. Cada adesivo utilizado no processo tem um único algarismo
de 0 a 9. Por exemplo, para fazer a numeração da peça número 100 são gastos três adesivos (um
algarismo 1 e dois algarismos 0). Sendo assim, o total de algarismos 9 que serão usados no processo
completo de numeração das peças é igual a
(A) 20.
(B) 10.
(C) 19.
(D) 18.
(E) 9.
12. (MPE/AM – Agente de Apoio – FCC) Considere a sequência numérica formada pelos números
inteiros positivos que são divisíveis por 4, cujos oito primeiros elementos são dados a seguir. (4, 8, 12,
16, 20, 24, 28, 32,...)
O último algarismo do 234º elemento dessa sequência é
(A) 0
(B) 2
(C) 4
(D) 6
(E) 8
Comentários
01. Resposta: D
Sabemos pelo enunciado que se trata de uma PA, ele quer descobrir quantos processos serão
protocolados no trigésimo dia, então será nosso a30, pela fórmula do termo geral temos que:
a30 = a1 + (30-1)r
a30 = a1 + 29r
Precisamos descobrir a razão, portanto vamos analisar os outros dados.
a1 = 5
a15 = 33
Utilizando o termo geral neste passo.
a15 = a1 + 14r
33 = 5 + 14r
33 – 5 = 14r
28 = 14r
r =
28
14
r = 2, agora podemos encontrar o que ele quer no exercício.
a30 = a1 + 29r
a30 = 5 + 29.2
a30 = 5 + 58 = 63
02. Resposta: Certo
Como serão devolvidos em forma de PA a partir de julho, teremos o seguinte, nem precisamos de
fórmula para resolver esta questão (Caso queira pode encontrar eles através do termo geral da PA).
Julho: 90
Agosto: 90 + 30 = 120
Setembro: 120 + 30 = 150
Outubro: 150 + 30 = 180
Novembro: 180 + 30 = 210
Dezembro: 210 + 30 = 240
Total devolvido até dezembro: 90 + 120 + 150 + 180 + 210 + 240 = 990 livros devolvidos (Pode utilizar
a fórmula da soma dos termos da PA se quiser)
Vamos encontrar o total de livros que foram emprestados
50 + 150 + 250 + 250 + 300 + 200 = 1200 livros emprestados.
Assim 1200 – 990 = 210 livros ainda faltam para ser entregues no ano de 2018 o que é mais que 200.

196
03. Resposta: A
Para resolver esta questão devemos descobrir que se trata de um PG pela dica deixada “feijão igual
ao triplo da quantidade colocada na caixa anteriormente escolhida” quando multiplica a razão será PG,
se fosse somada a razão seria uma PA.
Enfim, temos 9 caixas vazias e essa PG será assim, 1, 3, 9, 27, 81, ... até chegar na nova caixa, então
é finita essa PG, como ele que saber a quantidade de grãos colocadas no total de caixas, teremos a soma
desta PG Finita.
𝑆𝑛 = 𝑎1.
𝑞𝑛−1
𝑞−1
, onde n = 9, q = 3 e 𝑎1 = 1
𝑆9 = 1.
39
− 1
3 − 1
=
39
− 1
2
04. Resposta: A
O próprio enunciado já diz que é uma PA, então vamos utilizar a fórmula do termo geral da PA, mas
primeiro vamos descobrir a razão.
r = 48 – 45 = 3
𝑎1 = 45
𝑎𝑛 = 𝑎1 + (𝑛 − 1)𝑟
𝑎99 = 45 + 98 ∙ 3 = 339
05. Resposta: D
Como temos uma subtração será uma PA decrescente, 𝑎1 = 0,3;𝑟 = −0,07
Termo Geral da PA:𝑎𝑛 = 𝑎1 + (𝑛 − 1)𝑟
Vamos calcular o valor do a4 e do a7 e depois soma-los.
𝑎4 = 0,3 + 3. (−0,07)
𝑎4 = 0,3 − 0,21 = 0,09
𝑎7 = 0,3 + 6. (−0,07)
𝑎7 = 0,3 − 0,42 = −0,12
𝑆 = 𝑎4 + 𝑎7 = 0,09 + (−0,12) = 0,09 − 0,12 = −0,03
06. Resposta: C
Se observar teremos uma PG de razão q = 2 e a1 = 1, portanto vamos encontrar o valor do a6 e do
a8, podemos fazer por fórmula e sem fórmula, pois os números são pequenos.
Fórmula do termo geral
𝑎𝑛 = 𝑎1. 𝑞𝑛−1
Assim:
𝑎6 = 1.26−1
= 25
= 32
𝑎8 = 1. 28−1
= 27
= 128
Se fosse sem fórmula basta ir multiplicando por 2 a soma e encontrar o sexto e oitavo termo: 1, 2, 4,
8, 16, 32, 64, 128
A soma fica: 32 + 128 = 160.
07. Resposta: E
Vamos utilizar o primeiro e terceiro temos para descobrir a razão desta PG.
𝑎𝑛 = 𝑎1 ∙ 𝑞𝑛−1
𝑎3 = 𝑎1 ∙ 𝑞2
100 = 4 ∙ 𝑞2
𝑞2
= 25
𝑞 = 5
Agora vamos calcular o valor do segundo e do quarto termos e depois soma-los.
𝑎2 = 𝑎1 ∙ 𝑞1
= 4 ∙ 5 = 20
𝑎4 = 𝑎1 ∙ 𝑞3
= 4 ∙ 53
= 4.125 = 500
𝑎2 + 𝑎4 = 20 + 500 = 520
08. Resposta: B
Pelos valores apresentados, é uma PG de razão 4
a64 = ?

197
a1 = 1
q = 4
n = 64
𝑎𝑛 = 𝑎1 ∙ 𝑞𝑛−1
𝑎𝑛 = 1 ∙ 463
= (22)63
= 2126
09. Resposta: D
Se estão em Progressão Geométrica, então:
𝑟1
𝑟
=
𝑟2
𝑟1
, ou seja, 𝑟1 . 𝑟1 = 𝑟 . 𝑟2.
Assim: 𝑟1
2
= 144
𝑟1 = √144 = 12 𝑐𝑚
Sabemos que r + r1 + r2 = 52. Assim:
𝑟 + 12 + 𝑟2 = 52
𝑟 + 𝑟2 = 52 − 12
𝑟 + 𝑟2 = 40
10. Resposta: C
Trata-se de uma Progressão Aritmética, cuja fórmula do termo geral é
𝑎𝑛 = 𝑎1 + (𝑛 − 1). 𝑟
𝑛 = 7; 𝑎1 = 11; 𝑟 = 15 − 11 = 4
Assim, 𝑎7 = 11 + (7 − 1). 4 = 11 + 6.4 = 11 + 24 = 35
11. Resposta: A
Vamos resolver este exercício sem fórmula, utilizando apenas o raciocínio lógico, mas também é
possível resolver com fórmula.
Número que tem 9 de 1 até 100 são:
09, 19, 29, 39, 49, 59, 69, 79, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98 e 99, assim em 20 vezes aparece
o algarismo 9.
Por fórmula ficará assim:
Pois começa no 9 e vai de 10 em 10 até chegar no 99.
99 = 9 + (𝑛 − 1)10
10𝑛 − 10 + 9 = 99
𝑛 = 10
Vamos tirar o 99 para ser contado a parte: 10-1=9
Agora vamos encontrar do 90 até 99.
99 = 90 + (𝑛 − 1). 1
𝑛 = 99 − 90 + 1 = 10
São 19 números que possuem o algarismo 9, mas o 99 possui 2
19+1=20
12. Resposta: D
Sabemos que a razão é 4 e que pela sequência teremos uma PA, assim:
r = 4
𝑎1 = 4
E como ele que saber o último algarismo do 234° termo, devemos encontrar o 𝑎234
Pela fórmula do termo geral:
𝑎𝑛 = 𝑎1 + (𝑛 − 1)𝑟
𝑎234 = 4 + 233 ∙ 4 = 936
Portanto, o último algarismo é 6.

03_Matematica Banco do Brasil.pdf

Mais conteúdo relacionado

Mais procurados

Semelhante a 03_Matematica Banco do Brasil.pdf

03_Matematica Banco do Brasil.pdf