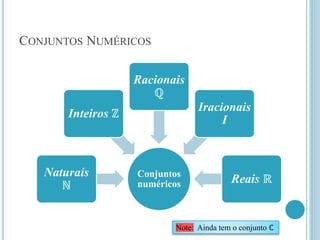
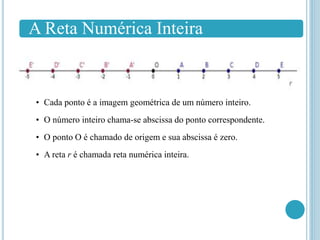
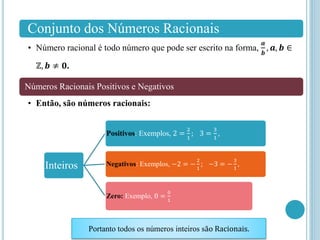
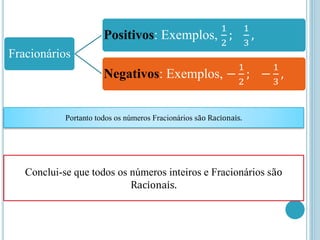
O documento aborda os conjuntos numéricos, incluindo números naturais, inteiros, racionais e suas propriedades. Ele descreve operações básicas como adição, subtração e multiplicação, detalhando regras e exemplos para cada operação. Além disso, discute a representação geométrica dos números e conceitos como módulo e números opostos.

1. MATEMÁTICA BÁSICA
Professor: Adino Santos
UNIVERSIDADE CATÓLICA TIMORENSE (UCT) SÃO
JOÃO PAULO II
Campus Central, Rua 12 de novembro Balide
Dili, Timor-Leste

2. CONJUNTOS NUMÉRICOS
Conjuntos
numéricos
Naturais
ℕ
Inteiros ℤ
Racionais
ℚ
Iracionais
I
Reais ℝ
Note: Ainda tem o conjunto ℂ

3. Conjuntos dos Números Naturais
• O conjunto dos números naturais é representado pela letra ℕ, e
seus números são indicados entre chaves: ℕ = 1,2,3,4, … .
• Alguns livros e autores de Matemática denem o conjunto dos
números naturais iniciando com o zero (0).
• Os números naturais formam uma sequência que "não tem
fim", ou seja, existem infitos números naturais. Usamos
reticências para indicar esse fato.

4. Números Inteiros Positivos e Números Inteiros Negativos
• Para todo número natural 𝒏:
• Um número +𝑛 (lê-se: mais +𝑛) chamado número inteiro positivo.
Exemplo: +1, +2, +3, … , são números inteiros positivos.
• Um número −𝑛 (lê-se: mais +𝑛) chamado número inteiro negativo.
Exemplo: −1, −2, −3, … , são números inteiros negativos.
• Reunindo os números inteiros negativos, o número zero e os números
inteiros positivos obtém-se o conjunto dos números inteiros, que se
representa pela letra ℤ (do alemao Zahl), e é escrito: ℤ =
{… , −3, −2, −1,0,1,2,3, … }

5. Subconjuntos de ℤ
• Sabemos que o conjunto dos números naturais ℕ é subconjunto dos
números inteiros ℤ. Existem outros subconjuntos importantes:

6. A Reta Numérica Inteira
• Cada ponto é a imagem geométrica de um número inteiro.
• O número inteiro chama-se abscissa do ponto correspondente.
• O ponto O é chamado de origem e sua abscissa é zero.
• A reta r é chamada reta numérica inteira.

7. Conjunto dos Números Racionais
• Número racional é todo número que pode ser escrito na forma,
𝒂
𝒃
, 𝒂, 𝒃 ∈
ℤ, 𝒃 ≠ 𝟎.
Números Racionais Positivos e Negativos
• Então, são números racionais:
Inteiros
Positivos: Exemplos, 2 =
2
1
; 3 =
3
1
,
Negativos: Exemplos, −2 = −
2
1
; −3 = −
3
1
,
Zero: Exemplo, 0 =
0
1
Portanto todos os números inteiros são Racionais.

8. Fracionários
Positivos: Exemplos,
1
2
;
1
3
,
Negativos: Exemplos, −
1
2
; −
1
3
,
Portanto todos os números Fracionários são Racionais.
Conclui-se que todos os números inteiros e Fracionários são
Racionais.

9. Números Decimais
• Um número racional também pode ser representado por um número
decimal exato ou periódico.
• Exemplos:
•
1
2
= 0,5;
3
2
= 1,5;
5
4
= 1,25; −
7
2
= −3,5 divide-se o
numerador pelo denominador da fração e obtém-se o número na forma
decimal.
•
2
3
= 0,6666 … = 0, 6;
•
4
9
= 0,4444 … = 0, 4;
•
23
99
= 0,232323 … = 0, 23;
Chamados de dízimas
periódicas
TPC : Como transformar as decimais dízimas periódicas para fração, 0, 6; 0, 4; 0, 23 ?

10. Representação Geométrica dos Números
Racionais
• Observe que os números inteiros e racionais podem ser representados por
pontos de uma reta.
 Os pontos que estão à direita do zero chamam-se positivos. Os pontos
negativos estão à esquerda do zero.
 Dados dois números quaisquer, o que está mais à direita é o maior deles, e o
que está mais à esquerda, o menor deles.

11. Exemplo:
Exercícios:
1. Preencha com os sinais, <, >, ≤, ≥, = .
0 … − 1; −10 … − 4;
2
3
…
1
3
; −
20
7
…
8
3

12. O Conjunto ℚ e Seus Subconjuntos
• O conjunto formado pelos números racionais positivos, pelo número zero
e pelos números racionais negativos chama-se conjunto dos números
racionais, que se representa pela letra ℚ.

13. Módulo ou Valor Absoluto …
• O módulo ou valor absoluto de um número inteiro ou racional é a
distância do número até a origem, isto é, é a distância do número até o
zero (0). Assim, o módulo de um número é sempre positivo.
• Um número, com exceção do zero, é formado de dois elementos:
• um sinal (+ 𝑜𝑢 −).
Exemplo
Os módulos de
+3 = 3 −3 = 3 −
4
5
=
4
5
−0,232 = 0,232 0 = 0

14. Números Opostos ou Simétricos
• Dois números (inteiros ou racionais) que possuem módulos iguais e
sinais diferentes são chamados números opostos ou simétricos.
Exemplo
Os módulos de
+3 = −3 = 3 −
4
5
= +
4
5
=
4
5
−0,2 = +0,2 = 0,2
Assim o simétricos de +3 é − 3 ; −
4
5
é +
4
5
; −0,2 é + 0,2
Observação: O simétricos de zero é o próprio zero.

15. Operações com Números Inteiros
Adição
• Caso.1: As parcelas tem o mesmo sinal
• A soma de dois números positivos é um número positivo e a soma de
dois números negativos é um número negativo.
Observação:
 Escrevemos a soma dos números inteiros sem colocar o sinal + da adição e
eliminamos os parênteses das parcelas.
 Na adição de números inteiros com sinais iguais, conserva-se os sinais e soma-se os
módulos.

16. Adição
• Caso.2: As parcelas tem sinais diferentes
• A soma de dois números inteiros de sinais diferentes é obtida
subtraindose os valores absolutos (módulos), dando-se o sinal do
número que tiver maior valor absoluto.
Observação:
o Escrevemos a soma dos números inteiros sem colocar o sinal + da adição e eliminamos
os parênteses das parcelas.
o Na adição de números inteiros com sinais diferentes, subtrai-se os módulos, dando-se o
sinal da parcela que tiver maior módulo.
Nota:
o Quando as parcelas são números opostos, a soma é igual a zero.
o Quando um dos números dados é zero, a soma é igual ao outro número.

17. Adição
• Caso.3: Soma de três ou mais números inteiros
• Calcula-se:
• a soma de todas as parcelas positivas;
• a soma de todas as parcelas negativas;
• a soma dos resultados obtidos conforme os casos anteriores
Exemplos:
.

18. Propriedades Estruturais da Adição
• Fechado: A soma de dois números inteiros é sempre um número
inteiro, isto é, ∀𝑎, 𝑏 ∈ ℤ: 𝑎 + 𝑏 ∈ ℤ.
• Comutativa: a ordem das parcelas não altera a soma, isto é, ∀𝑎, 𝑏 ∈
ℤ: 𝑎 + 𝑏 = 𝑏 + 𝑎
• Elemento neutro: o número zero é o elemento neutro da adição, ou seja,
∀𝑎 ∈ ℤ: 𝑎 + 0 = 𝑎
• Associativa: na adição de três números inteiros, podemos associar os
dois primeiros ou os dois últimos, sem que isso altere o resultado. Isto é,
∀𝑎, 𝑏, 𝑐 ∈ ℤ ∶ 𝑎 + 𝑏 + 𝑐 = 𝑎 + (𝑏 + 𝑐).
• Elemento simétrico: qualquer número inteiro admite um simétrico ou
oposto. Ou seja, ∀𝑎 ∈ ℤ ∶ 𝑎 + −𝑎 = 0
.

19. Operações com Números Inteiros
Subtração:
• É uma operação inversa à da adição.
• Para subtrairmos dois números inteiros, basta que adicionemos ao
primeiro o oposto do segundo.
• Exemplos:
• +9 − +4 = +9 + −4 = 9 − 4 = 5
• −7 − +9 = −7 + −9 = −7 − 9 = −16
• +6 − −3 = +6 + +3 = 6 + 3 = 9
• Obs: A subtração é fechado no conjunto ℤ.

20. Eliminação de Parênteses Precedidos de Sinal Negativo
• Para facilitar o cálculo, eliminamos os parênteses usando o signicado do
oposto.
• Exemplos:
Podemos reprensentar de modo mais simples uma adição de números inteiros.
o Eliminam-se o sinal de + da operação e os parênteses das parcelas;
o Escrevem-se as parcelas, uma em seguida à outra, cada qual com o próprio sinal.

21. Cálculo da Adição Algébrica
• Observe os exemplos:
Mais Exemplos:
Quando o sinal + precede um parentese
então mantem-se o sinal e número que
estão dentro do parentese.
Quando o sinal - precede um parentese
então inverte-se o sinal com número
dado.

22. Simplicação de Expressões Numéricas
• Eliminando parênteses, colchetes e chaves, calcular as somas
algébricas:
• Para a eliminação de colchetes e chaves valem as regras do item anterior.
• A eliminação de um sinal de associação se faz a partir do mais interno.
• Exemplo:
Exercicios:
1. 2 − −2 + 5 − 2 + 5 − 2
2. 1 − {3 − [1 + 3 − 5 + 4 + 10}
3. 20 − {27 + −4 − −2 + 13 − 9}

23. Multiplicação (× 𝑜𝑢 ∙)
• Se os fatores têm o mesmo sinal, o produto é positivo.
• Se os fatores têm sinais diferentes, o produto é negativo.
Exemplo:
a. 3 ∙ 8 = 24
b. −2 × 5 = −10
c. −3 ∙ 4 ∙ −2 ∙ −1
d. 2 × −3 × 3 × (−6)

24. Propriedades Estruturais da Multiplicação
• Fechado: o produto de dois números inteiros é sempre um nú-mero
inteiro.
• Comutativa: a ordem dos fatores não altera o produto.
• Elemento Neutro: o número +1 é o elemento neutro da multiplicação.
• Associativa: na multiplicação de três números inteiros, podemos associar
os dois primeiros ou os dois últimos, sem que isso altere o resultado.
• Distribuitiva: para multiplicar um número inteiro por uma soma
algébrica, podemos multiplicar o número por cada uma das parcelas e
adicionar, a seguir, os resultados obtidos.