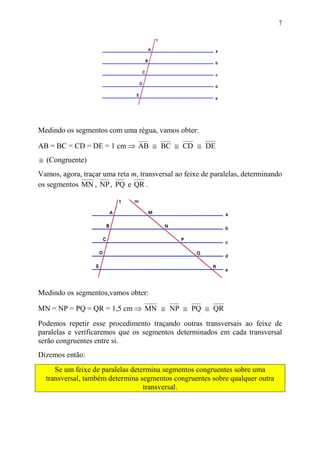
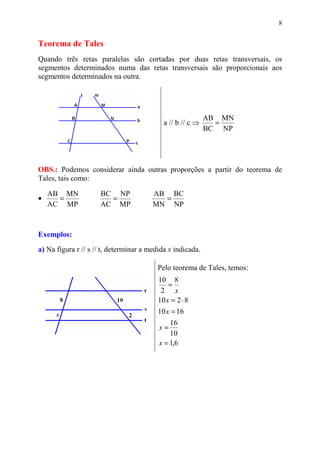
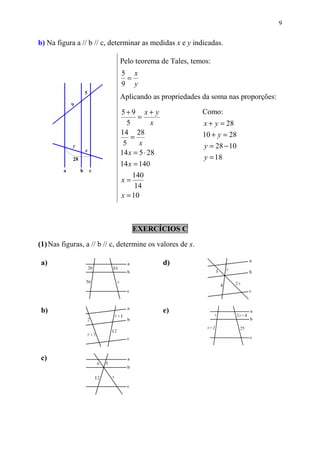
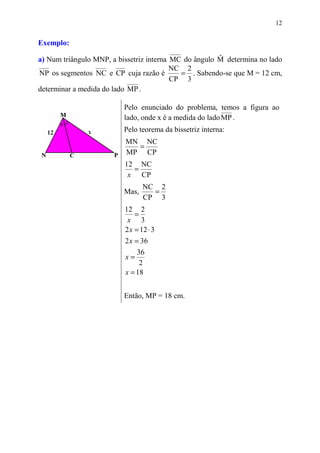
1) O documento apresenta informações sobre razão e proporção, propriedades de proporções, razão entre segmentos e segmentos proporcionais. 2) Também discute feixes de retas paralelas e o teorema de Tales, além de aplicações desse teorema e da bissetriz interna de um triângulo. 3) Fornece referências bibliográficas no final.

1. Segmentos proporcionais
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
Razão e proporção........................................................................................................... 1
Propriedades das proporções .................................................................................... 2
Propriedade fundamental ...................................................................................... 2
Propriedade da soma ............................................................................................. 2
Propriedade da diferença ...................................................................................... 2
Razão de dois segmentos ................................................................................................ 3
Segmentos proporcionais ................................................................................................ 5
Feixe de retas paralelas ................................................................................................... 6
Propriedades de um feixe de retas paralelas............................................................. 6
Teorema de Tales ............................................................................................................ 8
Aplicações do teorema de Tales ................................................................................... 10
Teorema da bissetriz interna de um triângulo ........................................................ 11
Referências bibliográficas............................................................................................. 14

2. 1
SEGMENTOS PROPORCIONAIS
Razão e proporção
A razão de dois números a e b, com b ≠ 0, é o quociente do primeiro pelo
a
segundo: a : b ou .
b
Por exemplo:
8 4
1) A razão entre 8 e 6 é 8 : 6 ou = .
6 3
20 4
2) A razão entre 20 e 15 é 20 : 15 ou = .
15 3
8 20
Nos exemplos acima, verificamos que as razões e são iguais:
6 15
8 4
=
6 3 8 20
⇒ =
20 4 6 15
=
15 3
8 20
Dizemos, então, que as razões e formam uma proporção ou, ainda, que os
6 15
números 8, 6, 20 e 15 são, nessa ordem, proporcionais.
Então:
Proporção é a igualdade entre duas razões.
Quatro números a, b, c e d (com b e d diferentes de zero) são, nessa ordem,
proporcionais quando a razão entre os dois primeiros é igual à razão entre os
dois últimos.
a c
=
b d

3. 2
a c
Em toda proporção = , temos:
b d
aed extremos
bec meios
Propriedades das proporções
Vamos ver algumas propriedades que são válidas para as proporções:
Propriedade fundamental
a c
= ⇒ a⋅d
{ = b⋅c
{
b d produto produto
dos extremos dos meios
Propriedade da soma
a c a+b c+d a+b c+d
= ⇒ = ou =
b d a c b d
Propriedade da diferença
a c a −b c−d a−b c−d
= ⇒ = ou =
b d a c b d

4. 3
EXERCÍCIOS A
(1) Em uma classe há 15 meninos e 20 meninas, num total de 35 alunos. A razão
entre o número de meninos e o número total de alunos da classe é indicada por
15 3
15:35 ou por . Seu valor na forma de fração irredutível é . Calcule em seu
35 7
caderno:
a) a razão entre o número de meninas e o total de alunos da classe;
b) a razão entre o número de meninos e o número de meninas;
c) a razão entre o número de meninas e o número de meninos.
(2) Use os números 18, 9, 4 e 8 e forme com eles uma proporção.
4 10
(3) Comprove as propriedades das proporções usando a proporção: = .
6 15
Razão de dois segmentos
Chamamos razão de dois segmentos a razão ou quociente entre os números que
exprimem as medidas desses segmentos, tomados na mesma unidade.
Exemplos:
a) Determinar a razão entre os segmentos AB e CD , sendo AB = 6 cm e
CD = 12 cm. (Lembre-se: AB representa a medida do segmento AB .)
AB 6 1
= =
CD 12 2
1
A razão é .
2
b) Dados MN e PQ , cujas medidas são, repectivamente, 2 cm e 5 cm,
determinar a razão ente MN e PQ .
MN 2
=
PQ 5
2
A razão é .
5

5. 4
c) Qual a razão entre os segmentos AB e DE , sabendo-se que AB = 2 m e
DE = 60 cm?
Nesse caso, precisamos, inicialmente, transformar as duas medidas para a
mesma unidade:
AB = 2 m = 200 cm
DE = 60 cm
AB 200 10
= =
DE 60 3
10
A razão é .
3
Você pode perceber, pelos exemplos, que a razão entre dois segmentos é sempre
um número real positivo.
Sendo um número real, a razão pode ser:
• um número racional → neste caso dizemos que os segmentos são
comensuráveis.
AB 1
= → AB e CD são segmentos comensuráveis
CD 6
{
número
racional
AB 10
= → AB e DE são segmentos comensuráveis
DE {3
número
racional
• um número irracional → neste caso dizemos que os segmentos são
incomensuráveis.
MN 2
= → MN e PQ são segmentos incomensuráveis
PQ 5
{
número
irracional

6. 5
Segmentos proporcionais
Pelas definições de proporção e razão de segmentos, podemos dizer que quatro
segmentos, AB , CD , EF e GH , nessa ordem, são proporcionais, quando a
razão entre os dois primeiros for igual à razão entre os dois últimos, ou seja:
AB EF
AB , CD , EF , GH são, nessa ordem, proporcionais, quando = .
CD GH
Lembre-se de que as medidas dos segmentos devem estar na mesma unidade pra
formar a proporção.
Exemplos:
a) Os segmentos AB = 4 cm, CD = 6 cm, EF = 8 cm e GH = 12 cm formam,
nessa ordem, uma proporção, pois:
AB 4
=
CD 6 AB EF
⇒ =
EF 8 4 CD GH
= =
GH 12 6
b) Quatro segmentos AB , MN , PQ e XY , nessa ordem, são proporcionais.
Se AB = 5 cm, MN = 15 cm e PQ = 4 cm, qual a medida de XY ?
AB PQ
Como AB , MN , PQ e XY são proporcionais ⇒ =
MN XY
AB 5 1
Mas = = .
MN 15 3
Então:
PQ 1
=
XY 3
4 1
=
XY 3
XY = 12 cm

7. 6
EXERCÍCIOS B
(1) Os segmentos da reta AB de 6 cm, MN de 15 cm, EF de 10 cm e PQ ,
nessa ordem, são segmentos proporcionais. Calcule a medida de PQ .
(2) AB , CD , CD e EF , nessa ordem, são segmentos proporcionais. Calcule a
medida de CD sabendo que AB = 9 cm e EF = 40 mm.
Feixe de retas paralelas
Você já sabe que duas retas de um plano são paralelas quando não possuem
pontos em comum, ou seja:
r // s
{ r ∩ s =∅
{
paralelas intersecção
Se tomarmos três ou mais retas paralelas entre si, obteremos um feixe de retas
paralelas, que denominaremos simplesmente feixe de paralelas.
Uma reta que corta um feixe de paralelas é denominada reta transversal.
feixe de retas paralelas:
r // s // m // u // v
t: transversal
Propriedades de um feixe de retas paralelas
Vamos considerar um feixe de retas paralelas cortadas por uma transversal t.
Assim, na transversal ficam determinados os segmentos AB , BC , CD e DE ,
como mostra a figura seguinte.

8. 7
Medindo os segmentos com uma régua, vamos obter:
AB = BC = CD = DE = 1 cm ⇒ AB ≅ BC ≅ CD ≅ DE
≅ (Congruente)
Vamos, agora, traçar uma reta m, transversal ao feixe de paralelas, determinando
os segmentos MN , NP , PQ e QR .
Medindo os segmentos,vamos obter:
MN = NP = PQ = QR = 1,5 cm ⇒ MN ≅ NP ≅ PQ ≅ QR
Podemos repetir esse procedimento traçando outras transversais ao feixe de
paralelas e verificaremos que os segmentos determinados em cada transversal
serão congruentes entre si.
Dizemos então:
Se um feixe de paralelas determina segmentos congruentes sobre uma
transversal, também determina segmentos congruentes sobre qualquer outra
transversal.

9. 8
Teorema de Tales
Quando três retas paralelas são cortadas por duas retas transversais, os
segmentos determinados numa das retas transversais são proporcionais aos
segmentos determinados na outra.
AB MN
a // b // c ⇒ =
BC NP
OBS.: Podemos considerar ainda outras proporções a partir do teorema de
Tales, tais como:
AB MN BC NP AB BC
• = = =
AC MP AC MP MN NP
Exemplos:
a) Na figura r // s // t, determinar a medida x indicada.
Pelo teorema de Tales, temos:
10 8
=
2 x
10 x = 2 ⋅ 8
10 x = 16
16
x=
10
x = 1,6

10. 9
b) Na figura a // b // c, determinar as medidas x e y indicadas.
Pelo teorema de Tales, temos:
5 x
=
9 y
Aplicando as propriedades da soma nas proporções:
5+9 x + y Como:
=
5 x x + y = 28
14 28
= 10 + y = 28
5 x y = 28 − 10
14 x = 5 ⋅ 28
y = 18
14 x = 140
140
x=
14
x = 10
EXERCÍCIOS C
(1) Nas figuras, a // b // c, determine os valores de x.
a) d)
b) e)
c)

11. 10
Aplicações do teorema de Tales
Consideremos o ∆ABC (Figura 1).
Vamos traçar uma reta r, paralela ao lado BC , que irá interceptar os lados AB e
AC nos pontos M e P, respectivamente (Figura 2).
Se traçarmos pelo ponto A uma reta s, paralela a r, obteremos três retas paralelas
( BC , r e s) e duas transversais ( AB e AC ).
r // s // BC
Pelo teorema de Tales:
AM AP
=
MB PC
Podemos enunciar, então:
Toda paralela a um lado de um triângulo que encontra os outros dois lados em
pontos distintos determina, sobre esses dois lados, segmentos que são
proporcionais.

12. 11
Exemplo:
a) Na figura abaixo, RS // BC . Determinar a medida de x.
Pelo teorema de Tales aplicado nos triângulos:
2x x + 4
=
x x +1
2 x( x + 1) = x( x + 4)
2x2 + 2x − x2 − 4x = 0
x2 − 2x = 0
x ( x − 2) = 0
x = 0 ou x − 2 = 0
x=2
Como x = 0 não serve, então x = 2.
Teorema da bissetriz interna de um triângulo
A bissetriz de um ângulo interno de um triângulo determina, sobre o lado
oposto, segmentos que são proporcionais aos lados do triângulo que formam o
ângulo considerado.
Se AS é bissetriz do ângulo Â, então:
AB BS AB AC
= ou =
AC SC BS SC

13. 12
Exemplo:
ˆ
a) Num triângulo MNP, a bissetriz interna MC do ângulo M determina no lado
NC 2
NP os segmentos NC e CP cuja razão é = . Sabendo-se que M = 12 cm,
CP 3
determinar a medida do lado MP .
Pelo enunciado do problema, temos a figura ao
lado, onde x é a medida do lado MP .
Pelo teorema da bissetriz interna:
MN NC
=
MP CP
12 NC
=
x CP
NC 2
Mas, =
CP 3
12 2
=
x 3
2 x = 12 ⋅ 3
2 x = 36
36
x=
2
x = 18
Então, MP = 18 cm.

14. 13
EXERCÍCIOS D
(1) Nos triângulos abaixo, determine a medida x indicada.
a) MN // BC c) DE // BC
b) PQ // AB d) AB // MP
(2) Nas figuras seguintes, determine o valor de x.
ˆ
a) AD é a bissetriz do ângulo A ˆ
c) BP é a bissetriz do ângulo B
ˆ
b) CM é a bissetriz do ângulo C ˆ
d) AD é a bissetriz do ângulo A

15. 14
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.