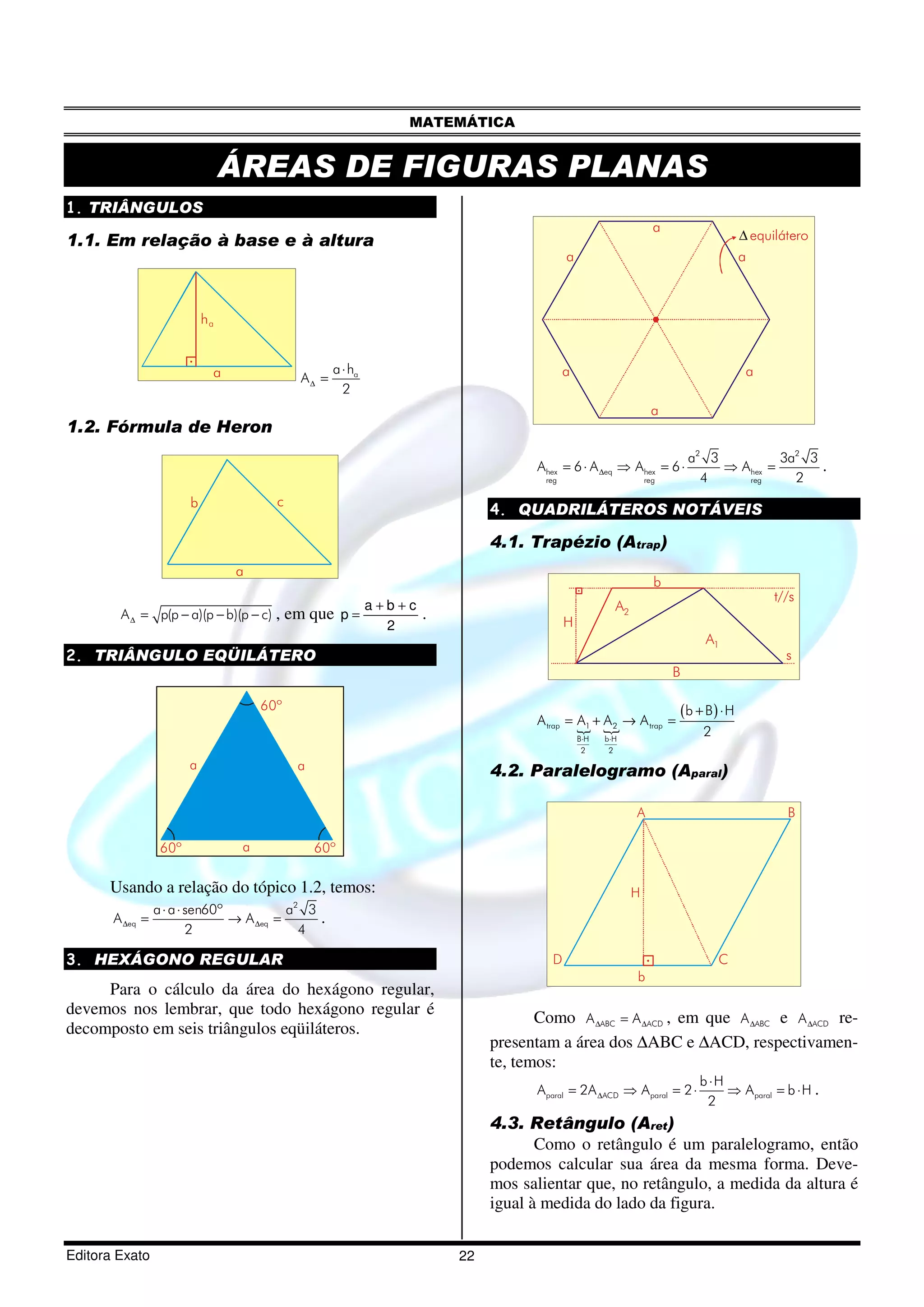
O documento discute áreas de figuras planas, incluindo triângulos, hexágonos regulares, quadriláteros notáveis como trapézios, paralelogramos e retângulos, losangos, quadrados e círculos. Ele fornece fórmulas para calcular a área dessas figuras e exemplos de exercícios resolvidos.

1. MATEMÁTICA
ÁREAS DE FIGURAS PLANAS
1. TRIÂNGULOS
a
1.1. Em relação à base e à altura ∆ equilátero
a a
ha
a a ⋅ ha a a
A∆ =
2
a
1.2. Fórmula de Heron
a2 3 3a2 3
A hex = 6 ⋅ A ∆eq ⇒ A hex = 6 ⋅ ⇒ A hex = .
reg reg 4 reg 2
b c
4. QUADRILÁTEROS NOTÁVEIS
4.1. Trapézio (Atrap)
a
b
t//s
a+b+c A2
A ∆ = p(p − a)(p − b)(p − c) , em que p = .
2 H
A1
2. TRIÂNGULO EQÜILÁTERO s
B
60º (b + B ) ⋅ H
A trap = A1 + A 2 → A trap =
{ { 2
B ⋅H b ⋅H
2 2
a a 4.2. Paralelogramo (Aparal)
A B
60º a 60º
Usando a relação do tópico 1.2, temos: H
a ⋅ a ⋅ sen60º a2 3
A ∆eq = → A ∆eq = .
2 4
3. HEXÁGONO REGULAR D C
b
Para o cálculo da área do hexágono regular,
devemos nos lembrar, que todo hexágono regular é
Como A ∆ABC = A ∆ACD , em que A ∆ABC e A ∆ACD re-
decomposto em seis triângulos eqüiláteros.
presentam a área dos ∆ABC e ∆ACD, respectivamen-
te, temos:
b ⋅H
A paral = 2A ∆ACD ⇒ A paral = 2 ⋅ ⇒ A paral = b ⋅ H .
2
4.3. Retângulo (Aret)
Como o retângulo é um paralelogramo, então
podemos calcular sua área da mesma forma. Deve-
mos salientar que, no retângulo, a medida da altura é
igual à medida do lado da figura.
Editora Exato 22

2. MATEMÁTICA
H R
AO = πR2.
b A ret = b ⋅ H
5.1. Setor Circular (As)
4.4. Losango (Alos)
A
B D d
Determinamos a área do setor circular pelas
regras de três, a seguir.
C
D
ângulo área Área Comp. do
arco
A los = A ∆ABD + A ∆BDC ,
em que A ∆ABC e A ∆BDC repre- 360º πR2 2πR2 2πR
sentam, respectivamente, as áreas dos ∆ABC e α As As l
∆BDC. ↓ ↓
D⋅d α ⋅ πR 2 l ⋅R
Alos = A ∆ABC + A ∆BDC ⇒ Alos = . As = As =
{ { 2 360º 2
D⋅ d 2 D⋅ d 2
2 2 Observação:
4.5. Quadrado (Aq) Se o ângulo α for medido em radianos, en-
A área do quadrado pode ser determinada por tão a área do setor circular ( A s ) é dada por
qualquer relação dos quadriláteros notáveis. Contudo, αR 2
normalmente calculamos essa área como sendo o .
2
quadrado da medida de seu lado.
5.2. Coroa Circular (ACC)
d
a
C R
r
d2
a aq= a2 = .
2
5. CÍRCULO (AO)
Considere dois círculos concêntricos (mesmo
Determinamos a área do círculo de raio R pela centro) de raios R e r (com R>r).
relação A O = πR 2 . A CC = A circulo − A circulo ⇒ A CC = πR 2 − πr 2 ⇒ A CC = π (R 2 − r 2 )
maior menor
Editora Exato 23

3. MATEMÁTICA
EXERCÍCIOS RESOLVIDOS 3 Um retângulo tem perímetro de 30m e as medi-
das de seus lados são números consecutivos. Qual
1 Determine a área do trapézio isósceles de períme- é a área deste retângulo?
tro 26cm, que possui a medida de suas bases i-
guais a 4cm e 12cm.
4
4 Um terreno tem área 450m2. Se o seu formato é
um trapézio, onde a “frente” e o seu “fundo” são
x x
H H I paralelos e iguais a 40m e 50m, qual a distância
entre esses lados?
4 4 4
Resolução:
2p = 4 + x + x + 12 = 26 ⇒ x = 5cm . 5 A diagonal de um quadrado mede 7 2cm . Qual a
Aplicando Pitágoras no ∆(I), temos: área deste quadrado?
x 2 = H2 + 42  H = 4cm
x =5
→
 
 4 + 12  ⋅ 4
{ { {
A trap =  b B  H → A = 32cm2 .
2
trap
6 A área da figura abaixo é (em cm2)
2 Calcule a área do quadrado de lado 5cm. 2cm
Resolução:
18cm
8cm
2cm
5cm
6cm
5cm
a) 160.
b) 180.
A = ( 5cm)2 = 25cm2 . c) 200.
d) 220.
e) 240.
EXERCÍCIOS
7 (CES/MS) Na figura a seguir, os segmentos AB ,
1 Qual a área de um trapézio de lados paralelos i- BC , DF e AF ¨têm as medidas indicadas em cen-
guais a 10cm e 18cm e altura 6cm? tímetros. O arco é uma semi-circunferência.
F E
2 A área de um retângulo é 18cm2 e um de seus la-
dos mede 0,2dm. Qual o seu perímetro em me- 3
tros? 4
1
D C
A B
3
Editora Exato 24

4. MATEMÁTICA
A área da figura é, em centímetros quadrados, i- 12 (FUVEST) Considere o triângulo representado
guais a: na malha quadriculada. A área do triângulo, em
a) 9 cm2, é:
π
b) 9 +
2
c) 9+π
d) 9 + 4π
4+π
e)
2
8 (UNICAMP) Uma folha retangular de cartolina
1cm
mede 35cm de largura por 75cm de comprimento.
Dos quatro cantos da folha, são cortados quatro 1cm
quadrados iguais, sendo que o lado de cada um
desses quadrados mede xcm de comprimento. a) 2.
a) Calcule a área do retângulo inicial. b) 3.
b) Calcule x de modo que a área da figura obtida, c) 4.
após o corte dos quatro cantos, seja igual a d) 5.
1.725cm2. e) 6.
9 Qual a área de um triângulo de lados 8cm, 12cm GABARITO
e 16cm?
1 84cm2
10 Calcule a área do triângulo destacado, sabendo 2 0,22
que ABCD é um retângulo cuja base e altura me-
3 56m2
dem, respectivamente, 12cm e 8cm e que
suur
CD ¨está dividido em quatro segmentos congru- 4 10m
entes, conforme a figura. 5 49cm2
B 12 C 6 220
π
7 9+
8 2
8
A D a) 2625
b) 15
9 12 15cm
11 (VUNESP) A área de um triângulo retângulo é
2
10 12cm
12dm2. Se um dos catetos é do outro, calcule a
3 11 2 13dm
medida da hipotenusa desse triângulo.
12 2
a) 2 13dm
b) 13 2dm
c) 8 3dm
d) 10 2dm
e) 13 5dm
Editora Exato 25

5. MATEMÁTICA
Editora Exato 26