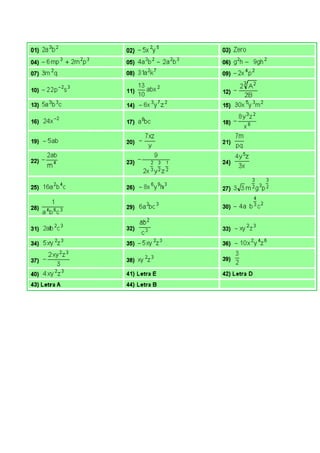
Este documento resume as operações entre monômios, incluindo adição, subtração, multiplicação, divisão, potenciação e radiciação. Cada operação segue regras específicas, como adicionar coeficientes algebricamente para adição e multiplicar todos os fatores para multiplicação. Exemplos ilustram como aplicar essas regras a monômios específicos.

1. Operações entre Monômios
1.0 - Adição de Monômios.
Só podemos adicionar monômios semelhantes e para tal conservamos a parte literal comum e adicionamos
algebricamente os
coeficientes numéricos
2.0 - Monômios Opostos, Simétricos ou Recíprocos.
Dois monômios semelhantes são opostos, simétricos ou recíprocos quando o coeficiente numérico de um é o
simétrico do coeficiente
numéricos do outro.
Os monômios são simétricos, pois os coeficientes numéricos são simétricos
Os monômios são simétricos, pois os coeficientes numéricos são
simétricos ou opostos
Importante : A soma de dois monômios simétricos é sempre igual a ZERO
3.0 - Subtração de Monômios.

2. Só podemos subtrair monômios semelhantes e para tal adicionamos o primeiro monômio com o simétrico do
segundo monômio.
4.0 - Multiplicação de Monômios.
Para multiplicarmos monômios devemos multiplicar todos os fatores presentes nos monômios. Lembremos
que para multiplicarmos
potencias de mesma base, conservamos a base e adicionamos seus expoentes.
5.0 - Divisão de Monômios.
Para dividirmos monômios devemos multiplicar o primeiro deles pelo inverso do segundo todos os fatores
presentes nos monômios.
Lembremos que para dividirmos potencias de mesma base, conservamos a base comum e diminuímos seus
expoentes. Uma forma

3. mais simples e rápida seria indicarmos o quociente entre o primeiro e o segundo monômio.
6.0 - Potenciação de Monômios.
Para elevarmos um monômio a uma potencia devemos elevar cada fator desse monômio a essa potencia. Na
prática elevamos o
coeficiente numérico à potencia e multiplicamos cada um dos expoentes das variáveis pelo expoente da
potencia.

4. 7.0 - Radiciação de Monômios .
Para extrairmos a raiz de um monômio efetuamos a raiz de seu coeficiente numérico e a raiz de cada um de
seus fatores, na prática
isso equivale a dividirmos cada expoente dos fatores pelo índice da raiz.
8.0 - Exercícios Resolvidos.

5. 9.0 - Exercícios Propostos.

7. VIII - Resolva as Questões Objetivas:

8. IX - Respostas dos Exercícios Propostos: