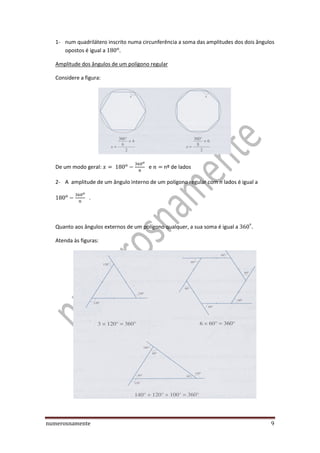
O documento discute vários tópicos sobre ângulos e triângulos, incluindo: 1) definições de ângulos complementares, suplementares e correspondentes; 2) classificações de triângulos de acordo com lados e ângulos; 3) propriedades de ângulos internos de triângulos e quadriláteros.

1. numerosnamente 1
Ângulos - Teoria
- Ângulos Complementares
Os ângulos são complementares, porque
- Ângulos Suplementares
Os ângulos são suplementares, porque
- Ângulo Giro
A soma dos ângulos
- Ângulos verticalmente Opostos
Os ângulos , são verticalmente opostos, porque

2. numerosnamente 2
- Ângulos Correspondentes
Os ângulos são correspondentes, pois
- Ângulos Alternos Internos
Os ângulos são alternos internos, pois
,
Classificação de Triângulos
Os triângulos podem classificar-se quanto aos lados:
- 3 lados iguais – Triângulo Equilátero
- 2 lados iguais – Triângulo Isósceles
- 3 lados diferentes – Triângulo Escaleno
Os triângulos podem classificar-se quanto aos ângulos:
- 1 ângulo agudo – Triângulo Acutângulo
- 1 ângulo reto – Triângulo Retângulo
- 1 ângulo Obtuso – Triângulo Obtusângulo
Sabe-se que:
A Soma dos ângulos internos de um triângulo é igual a

3. numerosnamente 3
Se um triângulo tem 2 lados iguais, também tem 2 ângulos iguais.
Se um triângulo tem os 3 lados iguais, também tem os três ângulos iguais.
Por exemplo:
Num quadrilátero, sabe-se que a soma dos seus ângulos internos é igual a .

4. numerosnamente 4
Estudo dos ângulos
- Ângulo ao Centro
Um ângulo ao centro é um ângulo que tem o vértice no centro da circunferência e os lados
contêm raios dessa mesma circunferência.
Por exemplo:
A amplitude de um ângulo ao centro é igual à amplitude do arco correspondente.
Por exemplo:
O ângulo ̂ ̂
Exemplo 1:
Considere a figura ao lado.
Calcule a amplitude do ̂ ?
Como o ̂ é um ângulo ao centro, então:
̂ ̂

5. numerosnamente 5
Exemplo 2:
Considere a figura ao lado:
Determine ?
- O ̂ =
- O triângulo ABO é isósceles pois os lados AO e BO são
iguais e tem o valor do raio da circunferência. Assim o triângulo
tem 2 ângulos iguais a ( ).
-
-
- Ângulo Inscrito
Chama-se ângulo inscrito a um ângulo com o vértice sobre a
circunferência e que cada lado contém uma corda.
Um ângulo inscrito define na circunferência dois arcos: um arco
menos e um arco maior. Ao arco compreendido entre os lados
chama-se arco correspondente.
Na figura a amplitude do ângulo inscrito é:
̂
̂
Exemplo 1:
Calcule a amplitude dos ângulos inscritos para as figuras a) e b)
a) ̂ =
̂
̂
b) ̂ ̂ ̂ ̂

6. numerosnamente 6
Exemplo 2:
Considere a figura ao lado, e determine a amplitude do ̂
- ̂
̂
̂
Propriedades:
1- Ângulos inscritos que têm o mesmo arco correspondente são iguais.
2- Um ângulo inscrito correspondente a uma circunferência é um ângulo reto.

7. numerosnamente 7
3- A ângulos ao centro iguais correspondem cordas iguais e correspondem arcos iguias e
reciprocamente
Tangentes a uma circunferência
1- Numa circunferência, uma reta tangente à circunferência é perpendicular a reta que
contem o centro e o ponto de tangência.
2- Numa circunferência, uma reta perpendicular ao meio de uma corda passa pelo centro
da circunferência.
A reta r contém o centro da circunferência

8. numerosnamente 8
3- Numa circunferência, os arcos e as cordas compreendidas entre as retas estritamente
paralelas são geometricamente iguais.
Polígonos inscritos numa circunferência
- Ângulos de um quadrilátero inscritos numa circunferência
Um triângulo pode ser sempre inscrito numa circunferência. O centro dessa circunferência
é o ponto de intersecção das mediatrizes dos lados do triângulo e o raio é a distância do
centro a um dos vértices
Nem todos os quadriláteros podem ser inscritos numa circunferência.
Considere a figura:
Conclui-se que

9. numerosnamente 9
1- num quadrilátero inscrito numa circunferência a soma das amplitudes dos dois ângulos
opostos é igual a
Amplitude dos ângulos de um polígono regular
Considere a figura:
De um modo geral: e nº de lados
2- A amplitude de um ângulo interno de um polígono regular com n lados é igual a
.
Quanto aos ângulos externos de um polígono qualquer, a sua soma é igual a
Atenda às figuras:

10. numerosnamente 10
3- A soma das amplitudes dos ângulos externos de um polígono qualquer é igual a