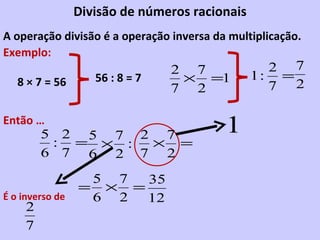
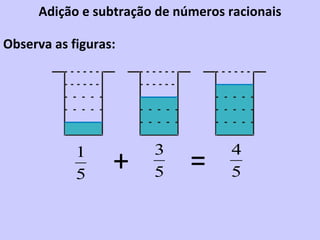
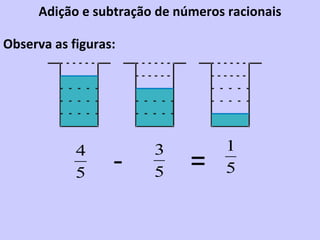
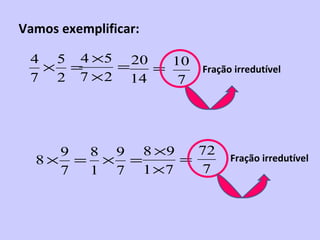
1) O documento discute operações com números racionais, incluindo adição, subtração, multiplicação, divisão e potenciação. 2) Para adicionar ou subtrair frações com o mesmo denominador, soma-se ou subtrai-se os numeradores e mantém-se o denominador. 3) Para multiplicar frações, multiplica-se os numeradores e também os denominadores.

1. OPERAÇÕES COM NÚMEROS RACIONAIS

2. Adição e subtração de números racionais Observa as figuras: + =

3. Adição e subtração de números racionais Observa as figuras: - =

4. Adição e subtração de números racionais Para adicionar ou subtrair dois números representados por frações com o mesmo denominador, adicionam-se ou subtraem-se os numeradores e o denominador mantém-se. + = - =

5. Adição e subtração de números racionais = + m.m.c.(6,4) = M 6 : 0, 6, 12, 18, 24, … M 4 : 0, 4, 8, 12, 16, 20, … (2) (3) = + = = 12 Então, vamos escrever frações equivalentes a e com denominador 12 .

6. A Maria comeu metade de um chocolate. O Paulo comeu a quarta parte de um chocolate igual ao da Maria . Logo o Paulo comeu metade de metade do chocolate que a Maria comeu . Ou seja, o Paulo comeu de Multiplicação de números racionais

7. de É o mesmo que Como se multiplicaram estes dois números? Multiplicámos os numeradores e multiplicámos os denominadores. Então: Para multiplicar dois números representados por frações, multiplicam-se os numeradores um pelo outro e multiplicam-se os denominadores, também, um pelo outro.

8. Vamos exemplificar: Fração irredutível Fração irredutível

9. Continuando a exemplificar… Generalizando…

10. Potência de um número racional É a base 3 É o expoente

11. Inverso de um número racional Dado um número racional diferente de zero, é sempre possível encontrar outro número que multiplicado pelo primeiro dê de produto a unidade (1). O inverso de 8 é O inverso de é e vice-versa. e vice-versa. Generalizando…

12. Divisão de números racionais A operação divisão é a operação inversa da multiplicação. Exemplo: 8 × 7 = 56 56 : 8 = 7 Então … É o inverso de

13. Para dividir dois números racionais, diferentes de zero, multiplica-se o dividendo pelo inverso do divisor Generalizando…