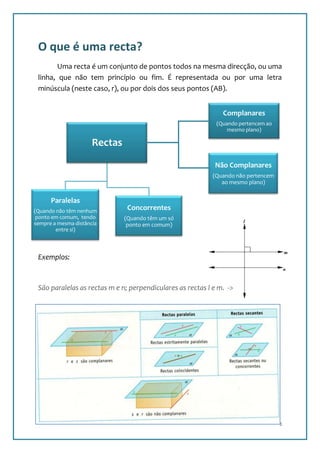
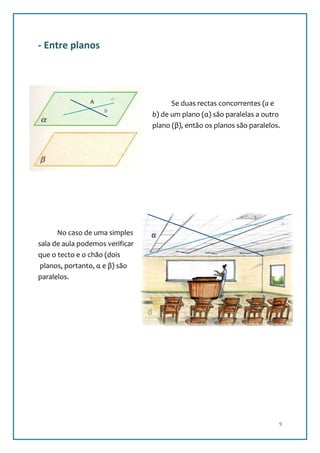
Este documento discute critérios de paralelismo e perpendicularidade entre retas e planos. Primeiro define retas e planos, e explica o que significa paralelismo e perpendicularidade. Em seguida, fornece critérios para determinar se retas e planos são paralelos ou perpendiculares, incluindo se duas retas em um plano são paralelas a outro plano, ou se uma reta é perpendicular a duas retas concorrentes em um plano. Exemplos ilustram como aplicar esses critérios na prática.

1. Escola dos 2ºe 3ºciclos D. João I da Baixa da Banheira
Critérios de Paralelismo e
Perpendicularidade entre
rectas e planos e entre
planos
Trabalho realizado por: Inês Gonçalves nº13, Joana Ferreira nº15, Pedro
Ribeiro nº23, Sara Candeias nº24
Ano/Turma: 9ºA
Professor: Francisco Louro
Ano Lectivo: 2010/2011
Disciplina: Matemática
0

2. Índice
Introdução …………………………………………………………….. Página 2
O que é uma recta? ……………………………………………………. Página 3
O que é um plano? ...…………………………………………. ………. Página 5
O que significa paralelismo? ………………………………………….. Página 6
O que significa perpendicularidade? ………….……………………… Página 7
Critérios de paralelismo:
- Entre rectas e planos ….………...…………………………….. Página 8
- Entre planos ……...……………………………………………. Página 9
Critérios de perpendicularidade:
- Entre rectas e planos ..………………………………...……... Página 10
- Entre planos ……..……………………………………………. Página 11
Conclusão ……………………………………………………………... Página 12
Bibliografia ……………………………………………………………. Página 13
1

3. Introdução
Este trabalho foi realizado no âmbito da disciplina de Matemática, a
pedido, do professor Francisco Louro.
Ao realizarmos este trabalho pretendemos enriquecer os nossos
conhecimentos matemáticos para que num futuro próximo nos possa vir a
ser útil.
A nossa intuição leva-nos, muitas vezes, a afirmar que dois planos são
paralelos ou que uma recta é perpendicular a um plano.
Como garantir que a nossa intuição está correcta?
Utilizando critérios de paralelismo e perpendicularidade.
2

4. O que é uma recta?
Uma recta é um conjunto de pontos todos na mesma direcção, ou uma
linha, que não tem princípio ou fim. É representada ou por uma letra
minúscula (neste caso, r), ou por dois dos seus pontos (AB).
Complanares
(Quando pertencem ao
mesmo plano)
Rectas
Não Complanares
(Quando não pertencem
ao mesmo plano)
Paralelas
(Quando não têm nenhum Concorrentes
ponto em comum, tendo (Quando têm um só
sempre a mesma distância ponto em comum)
entre si)
Exemplos:
São paralelas as rectas m e n; perpendiculares as rectas l e m. ->
3

5. Podemos observar rectas em praticamente todas as situações do
quotidiano:
Em qualquer um dos degraus destas
escadas podemos observar rectas, como
também o podemos fazer no chão ou até
mesmo no corrimão.
Na cozinha, tanto nos
armários, como nas bancadas, e
até nas prateleiras.
No parque infantil, tanto no
escorrega, nos baloiços, no
caixote do lixo… em tudo,
praticamente.
4

6. O que é um plano?
Um plano é um objecto geométrico infinito a duas dimensões.
Representa-se normalmente por um paralelogramo e identifica-se por uma
letra grega ou por três dos seus pontos não colineares.
Exemplos de planos na vida real:
Numa baliza simples de
futebol, podemos observar três
planos, onde dois são paralelos.
5

7. O que significa paralelismo?
Paralelismo é uma noção que indica se dois objectos (rectas ou planos)
estão na mesma direcção, com a mesma distância entre si (em qualquer
ponto dos seus pontos), sem nunca se tocarem.
Exemplos de paralelismo na vida real:
- Estes lápis de cor estão colocado
de forma a ficarem paralelos uns aos
outros (representa rectas paralelas);
- Nesta vedação, por exemplo,
verificamos que todos os barrotes
verticais estão paralelos uns aos outros,
e que ambas as tábuas horizontais
também o estão. (de novo, representa
rectas);
- Neste quarto podemos
verificar que as paredes são
paralelas duas a duas, estando,
neste caso, representadas por
cores;
6

8. O que significa perpendicularidade?
Perpendicularidade é uma noção que indica se dois objectos (rectas ou
planos) fazem um ângulo de 90º entre si.
Duas rectas podem ser perpendiculares, tal como dois planos o podem
ser, mas pode uma recta ser perpendicular a um plano? Sim, pode.
Neste caso são duas rectas (s e r) perpendiculares, ou no caso da
janela, várias (10 rectas) perpendiculares.
Dois planos (α e β) perpendiculares; dois livros perpendiculares.
Uma recta perpendicular a um plano; uma vara perpendicular à água.
7

9. Critérios de paralelismo
É fácil observar e verificar que duas rectas ou dois planos são
paralelos, mas para o justificar é necessário enunciar teoremas a que se
chamam critérios de paralelismo (entre rectas e planos, obviamente).
- Entre rectas e planos
a
Se existir num plano uma recta
paralela a uma recta dada complanar (ou
b seja, que não está contida nesse plano),
a recta e o plano são paralelos.
No caso de uma baliza, a
acontece isso mesmo, tendo em
atenção a recta a, e a recta b que
está contida no plano α, o que torna
a recta a paralela ao plano α.
α b
8

10. - Entre planos
a
A Se duas rectas concorrentes (a e
b
b) de um plano (α) são paralelas a outro
plano (β), então os planos são paralelos.
a
No caso de uma simples α
sala de aula podemos verificar
que o tecto e o chão (dois
planos, portanto, α e β) são
paralelos.
b
β
9

11. Critérios de perpendicularidade
É igualmente fácil observar que duas rectas ou dois planos são
perpendiculares, mas, mais uma vez, para o justificar é necessário enunciar
os critérios de perpendicularidade (de novo entre rectas e planos,
obviamente).
- Entre rectas e planos
Se uma recta (r) é perpendicular a
duas rectas concorrentes (a e b) de um
plano (α), então a recta (r) é
perpendicular ao plano.
r
a
r
Considerando a árvore a
a
recta perpendicular (r) às duas
rectas concorrentes, esta acaba
por ser perpendicular ao plano
(chão, representado por α).
a
α b
10

12. - Entre planos
Se num plano (α) existe um recta
perpendicular (t) a outro plano (β),
então os planos são perpendiculares.
t
a
α
α β
β
Denominando a parede lateral da casa como plano α e a parede frontal
como plano β, temos assim dois planos perpendiculares.
11

13. Conclusão
Através da realização deste trabalho pudemos compreender uma das
bases mais importantes para construção da geometria.
Um critério é uma afirmação que necessita de demonstração para ser
considerada verdadeira e, com estes simples conhecimentos aqui explícitos,
conseguimos confirmar e provar o paralelismo e a perpendicularidade de
objectos, com uma certa facilidade.
12

14. Bibliografia
Para a realização destes trabalhos recorremos às seguintes fontes:
I – Manuais:
- Neves, Maria Augusta Ferreira; Guerreiro, Luís; Neves, Armando
“Matemática”, 2ª Parte 9ºano, 1ª edição, Porto Editora, 2009.
II – Internet:
- http://geomdesc.no.sapo.pt/pag6.htm
- http://www.educ.fc.ul.pt/icm/icm98/icm22/representa.htm
- http://www.google.pt
13