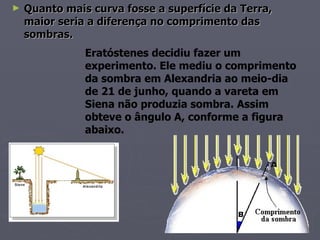
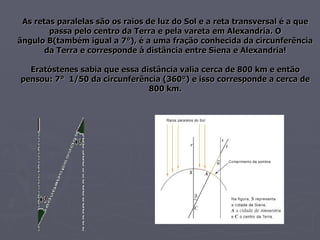
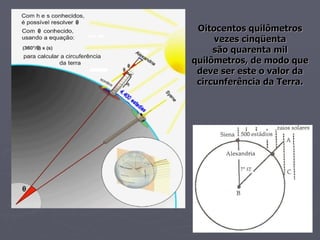
Eratóstenes mediu a sombra de uma vareta em Alexandria no solstício de verão e descobriu que ela formava um ângulo de 7° com a sombra de outra vareta 800 km mais ao sul. Isso significava que a circunferência da Terra era aproximadamente 50 vezes maior que a distância entre as varetas, ou cerca de 40.000 km.

1. Eratóstenes e a Terra. A circunferência da Terra.

2. ERATÓSTENES VIVEU NO EGITO ENTRE OS ANOS 276 E 194 ANTES DE CRISTO. Ele era bibliotecário-chefe da famosa Biblioteca de Alexandria, e foi lá que encontrou, num velho papiro, indicações de que ao meio-dia de cada 21 de junho na cidade de Siena, 800 km ao sul de Alexandria, uma vareta fincada verticalmente no solo não produzia sombra. Se o mundo é plano como uma mesa, então as sombras das varetas têm de ser iguais. Se isto não acontece é porque a Terra deve ser curva!

3. Quanto mais curva fosse a superfície da Terra, maior seria a diferença no comprimento das sombras. Eratóstenes decidiu fazer um experimento. Ele mediu o comprimento da sombra em Alexandria ao meio-dia de 21 de junho, quando a vareta em Siena não produzia sombra. Assim obteve o ângulo A, conforme a figura abaixo.

4. As retas paralelas são os raios de luz do Sol e a reta transversal é a que passa pelo centro da Terra e pela vareta em Alexandria. O ângulo B(também igual a 7°), é a uma fração conhecida da circunferência da Terra e corresponde à distância entre Siena e Alexandria! Eratóstenes sabia que essa distância valia cerca de 800 km e então pensou: 7° 1/50 da circunferência (360°) e isso corresponde a cerca de 800 km.

5. Oitocentos quilômetros vezes cinqüenta são quarenta mil quilômetros, de modo que deve ser este o valor da circunferência da Terra.

6. Escola Estadual Fernando Corrêa Data: 12/04/2010 Alunos: Alaor, Luiz Felipe, José Paulo e Daniele. N°: 03, 25, 20 e 07 Professor: Amôr Josê Miguel dos Santos Matéria: Matemática