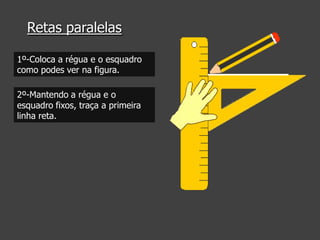
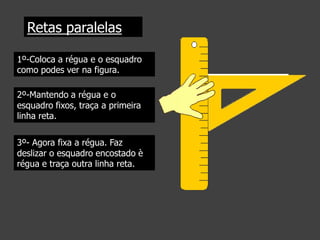
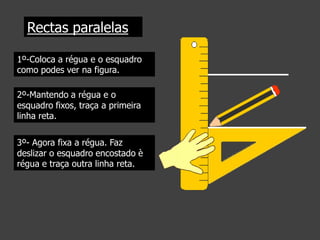
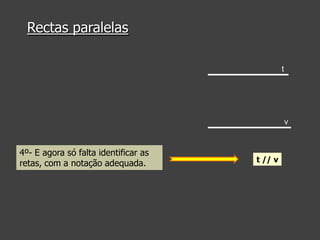
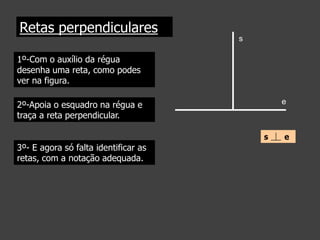
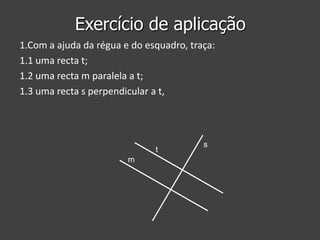
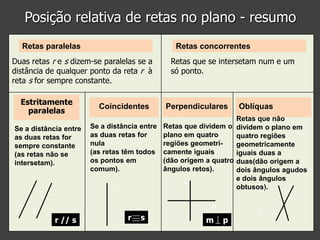
Este documento apresenta conceitos geométricos básicos como ponto, reta, semirreta e segmento de reta. Explica como representar estas figuras e descreve suas posições relativas no plano, nomeadamente retas paralelas, perpendiculares e concorrentes. Inclui instruções passo-a-passo para traçar retas paralelas e perpendiculares com régua e esquadro.

1. Escola Básica Nº 2 da Lousã
Departamento de Matemática e Ciências
Experimentais
Posição relativa de retas, semirretas e segmentos
de reta no plano
5º Ano

2. “A
marca de uma
ponta de lápis bem
fina no papel dá a
ideia do que é um
ponto. Toda figura
geométrica é
considerada um
conjunto de pontos.”
Ponto P

3. Sucessão infinita de pontos
colineares
r
A superfície de uma mesa é plana.
Imagine que tal superfície,
conservando-se plana, se estenda
infinitamente em todas as
direções.
A nova superfície assim obtida é
um plano.
Os planos são representados por letras gregas minúsculas.
Por exemplo:
 (alfa),  (beta) e  (gama).

4. Reta – É um conjunto infinito de pontos com a
mesma direcção
Uma reta pode representar-se de duas formas:
através de uma letra minúscula,
através de duas letras maiúsculas, AB
Uma reta pode prolongar-se
infinitamente nos dois sentidos
s

5. Uma semirreta tem origem num ponto e pode
prolongar-se infinitamente num dos sentidos
F
E
Representa-se por:
duas letras maiúsculas com um ponto sobre a letra onde se
inicia a semirreta.
F E - A semirreta FE tem origem em F e passa por E
escrevendo:
semirreta F E

6. Um segmento de reta tem início num ponto e fim noutro.
P
Representa-se por:
Q
duas letras maiúsculas dentro de parênteses retos.
[PQ]
ou
[QP]
Escrevendo:
segmento de reta PQ
ou segmento de reta QP

7. P
Q
O comprimento do segmento de reta representa-se por:
PQ
ou
QP

8. Exercício de aplicação
1.Observa a figura e, usando a notação científica adequada,
identifica os segmentos de reta, as semirretas e as retas.
• Segmentos de recta
• Semirretas
• Retas
[XY] e [EU] ou segmento de reta XY e EU
OA e TZ ou semirreta OA e semirreta TZ
reta s, reta v
e
reta PQ

9. Posição relativa de retas no plano
Observa com atenção os campos representados:
s
Duas retas de um plano
s
são concorrentes se têm
r
um e um só ponto comum.
Retas
concorrentes
perpendiculares
b
Retas
concorrentes
oblíquas

10. Vamos agora observar outros dois campos de
futebol:
t
u
Duas retas de um plano
c
são paralelas se não têm
nenhum ponto comum
ou se são coincidentes.
Retas
estritamente
paralelas
d
Retas
coincidentes

11. Posição relativa de retas no plano - resumo
Retas paralelas
Retas concorrentes
Duas retas r e s dizem-se paralelas se a
distância de qualquer ponto da reta r à
reta s for sempre constante.
Estritamente
paralelas
Se a distância entre
as duas retas for
sempre constante
(as retas não se
intersetam).
r
Coincidentes
Retas que se intersetam num e um
só ponto.
Perpendiculares
Retas que não
Se a distância entre Retas que dividem o dividem o plano em
as duas retas for
plano em quatro
quatro regiões
nula
regiões geometrigeometricamente
(as retas têm todos camente iguais
iguais duas a
os pontos em
(dão origem a quatro duas(dão origem a
comum).
ângulos retos).
dois ângulos agudos
e dois ângulos
m
r
obtusos).
n
p
s
r // s
Oblíquas
s
r
s
m
p
h

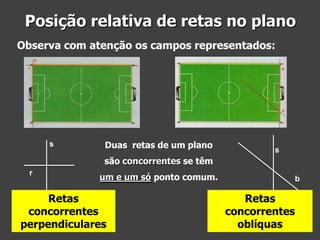
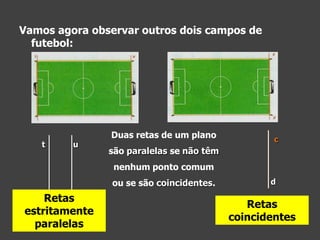
12. Exercício de aplicação
1.Observa a figura e indica
usando a notação adequada:
1.1 um segmento de reta
[AE] , por exemplo
1.2 duas retas perpendiculares
CD e AE , por exemplo
1.3 duas retas paralelas
AC e DE
1.4 duas retas oblíquas
BE e DE, por exemplo

13. Como traçar retas paralelas? E retas
perpendiculares?
Para traçar retas paralelas e retas perpendiculares
precisas de uma régua, de um esquadro e um lápis
como é óbvio!!!E já agora convém ter a borracha
por perto…
Segue as instruções e mãos à obra!!!

14. Retas paralelas
1º-Coloca a régua e o esquadro
como podes ver na figura.
2º-Mantendo a régua e o
esquadro fixos, traça a primeira
linha reta.

15. Retas paralelas
1º-Coloca a régua e o esquadro
como podes ver na figura.
2º-Mantendo a régua e o
esquadro fixos, traça a primeira
linha reta.
3º- Agora fixa a régua. Faz
deslizar o esquadro encostado è
régua e traça outra linha reta.

16. Rectas paralelas
1º-Coloca a régua e o esquadro
como podes ver na figura.
2º-Mantendo a régua e o
esquadro fixos, traça a primeira
linha reta.
3º- Agora fixa a régua. Faz
deslizar o esquadro encostado è
régua e traça outra linha reta.

17. Rectas paralelas
t
v
4º- E agora só falta identificar as
retas, com a notação adequada.
t // v

18. Retas perpendiculares
1º-Com o auxílio da régua
desenha uma reta, como podes
ver na figura.

19. Retas perpendiculares
1º-Com o auxílio da régua
desenha uma reta, como podes
ver na figura.
2º-Apoia o esquadro na régua e
traça a reta perpendicular.

20. Retas perpendiculares
s
1º-Com o auxílio da régua
desenha uma reta, como podes
ver na figura.
e
2º-Apoia o esquadro na régua e
traça a reta perpendicular.
s
3º- E agora só falta identificar as
retas, com a notação adequada.
e

21. Exercício de aplicação
1.Com a ajuda da régua e do esquadro, traça:
1.1 uma recta t;
1.2 uma recta m paralela a t;
1.3 uma recta s perpendicular a t,
t
m
s

22. Fim