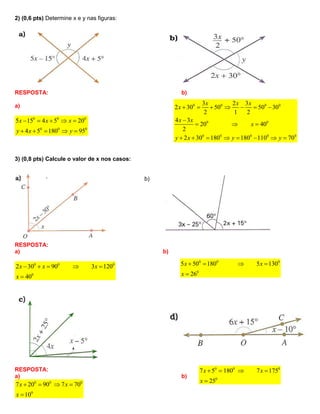
Este documento contém um teste de geometria com 8 questões para alunos do 8o ano. As questões abordam tópicos como determinar valores numéricos em figuras geométricas, calcular ângulos, classificar afirmações sobre ângulos como verdadeiras ou falsas, e calcular medidas de ângulos a partir de suas propriedades. O teste é avaliado com nota de 0 a 4 e tem instruções sobre como preencher e entregar a avaliação.

1. 2º TESTE DE GEOMETRIA – 8º ANO (1º BIMESTRE).
TERESÓPOLIS, 04 DE ABRIL DE 2012.
NOME: _________________________________________Nº: ________
PROF: CARLOS JOSÉ GOMES LOURENÇO TURMA: _________
Orientações: Erros ortográficos: ____
Antes de começar responder, leia as questões propostas com muita atenção. Valor da Avaliação: 4,0
A avaliação deverá ser entregue com as respostas feitas a caneta (azul ou preta).
Não rasure, pois não é permitido o uso de corretivos. Extra: 0,5
Havendo cálculos, o desenvolvimento do raciocínio deve estar exposto, claro. NOTA:__________
Não será permitido o uso de calculadoras.
Fique atento aos erros ortográficos, pois eles serão descontados
Use o verso para os cálculos, se necessitar.
As questões de múltipla escolha só serão aceitas, mediante apresentação do desenvolvimento.
Boa avaliação!!!
1) (0,6 pts) Determine o valor de x e a medida do ângulo AÔB nas figuras a seguir, sendo OP bissetriz.
a) b)
RESPOSTA:
a) b) Temos duas equações:
3x 3x
3x  300   150  3x   150  300 2 y  y  100  x  100 1800 e x  100  y  100
4 4
12 x  3x 1800
 450  9 x 1800  x  Assim:
4 9
x  20 0 ˆ  2.(3x  300 )  600
 AOB  x  3 y  1800 (1)

  substutuindo (2) em (1) temos :
 x  y  20 (2)
0

2000
y  20  3 y  180  4 y  200  y 
0 0 0
4
y  50 0
e x  30 0
ˆ ˆ
AOB  2 y  AOB  1000

2. 2) (0,6 pts) Determine x e y nas figuras:
RESPOSTA: b)
3x 2 x 3x
a) 2 x  300   500    500  300
2 1 2
5 x  150  4 x  50  x  200 4 x  3x
 200  x  400
y  4 x  50  1800  y  950 2
y  2 x  300  1800  y  1800  1100  y  700
3) (0,8 pts) Calcule o valor de x nos casos:
b)
RESPOSTA:
a) b)
2 x  300  x  900  3x  1200 5 x  500  1800  5 x  1300
x  400 x  260
RESPOSTA: 7 x  50  1800  7 x  1750
a) b)
x  250
7 x  20  90  7 x  70
0 0 0
x  100

3. 4) (0,8 pts) Classifique em verdadeiro (V) ou falso (F), justificando as falsos.
a) Dois ângulos consecutivos são adjacentes. ( F ) Dois ângulos adjacentes são consecutivos.
b) Dois ângulos adjacentes são opostos pelo vértice. ( F ) Não, pois não possuem semirretas em comum.
c) Dois ângulos opostos pelo vértice são congruentes. ( V )
d) Dois ângulos opostos pelo vértice são consecutivos. ( F ) Não, pois não possuem semirretas em comum.
e) Dois ângulos suplementares podem ser adjacentes. ( V )
f) Dois ângulos complementares são adjacentes. ( F ) Podem ser, mas não significa que sempre serão.
g) Os ângulos de medida 15º, 25º e 50º são complementares. ( F ) A definição diz dois ângulos e não dois ou mais.
h) Dois ângulos adjacentes são congruentes. ( F ) Podem ser, mas não significa que sempre serão.
5) (0,4 pts) Determine o ângulo cuja medida é o dobro do seu suplemento.
RESPOSTA:
x  2.(1800  x)  x  3600  2 x  x  2 x  3600
3600
3x  3600  x  x  1200
3
6) (0,5 pts) Somando-se a medida do complemento com a medida do suplemento de um ângulo obtém-se
130°. Calcule esse ângulo.
RESPOSTA:
900  x  1800  x  1300  2 x  2700  1300  2700  1300  2 x
1400
1400  2 x  x  x  700
2

4. 7) (0,4 pts) A metade de um ângulo menos a quinta parte do seu complemento mede 45°. Qual é esse ângulo?
RESPOSTA:
x (900  x) 5 x  2.(900  x)
  450   450  5 x  1800  2 x  4500
2 5 10
6300
7 x  4500  1800  x  x  900
7
8) (0,4 pts) O ângulo cujo suplemento excede de 6° o quádruplo do seu complemento, é:
a) 58° RESPOSTA:
b) 60°
1800  x  4.(900  x)  60  1800  x  3600  4 x  60  4 x  x  3660  1800
c) 62° 1860
3x  1860  x  x  620
d) 64° 3
e) 68°