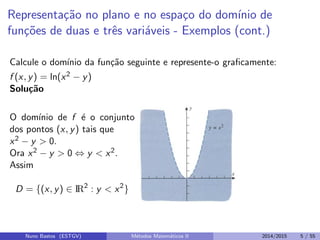
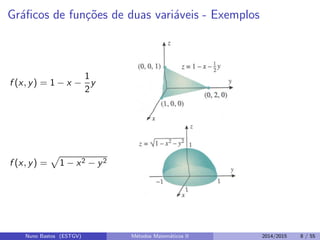
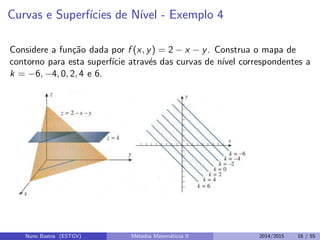
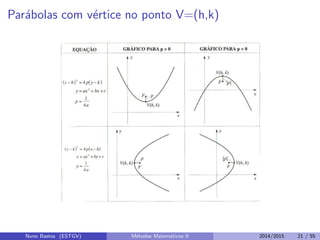
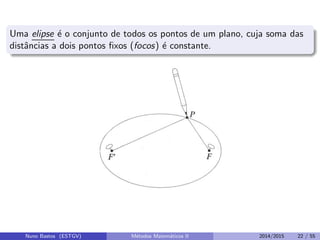
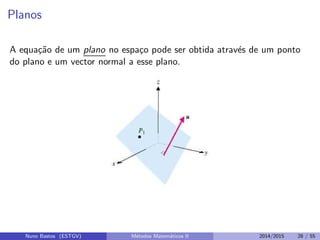
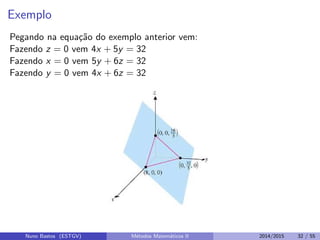
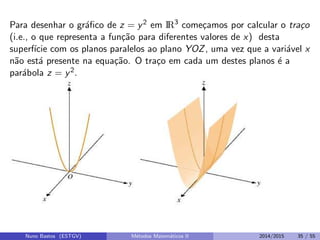
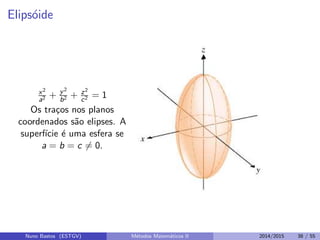
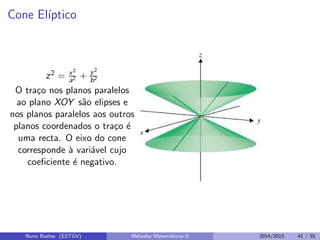
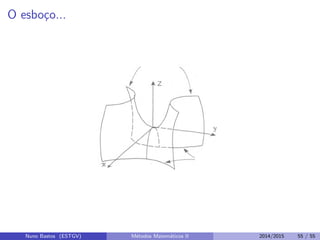
Este documento apresenta um capítulo sobre funções reais de duas ou mais variáveis reais. Apresenta exemplos de funções de duas e três variáveis, define formalmente o que é uma função de n variáveis reais e explica a representação gráfica do domínio e do gráfico destas funções. Explora ainda curvas e superfícies de nível, exemplos de seções cônicas e esboços de gráficos usando curvas de nível.

1. M´etodos Matem´aticos II
Nuno Bastos
Licenciatura em Tecnologias e Design de Multim´edia
Escola Superior de Tecnologia e Gest˜ao de Viseu
Gabinete 42
2014/2015
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 1 / 55

2. Neste cap´ıtulo iremos estudar fun¸c˜oes reais de duas ou mais vari´aveis reais.
Exemplos
1 A ´area de um triˆangulo depende das vari´aveis base e altura:
A△(b, h) =
b · h
2
2 O volume de uma caixa com laterais rectangulares depende de trˆes
dimens˜oes x, y e z:
V (x, y, z) = x · y · z
3 A m´edia aritm´etica x de n n´umeros x1, x2, . . . , xn ´e uma fun¸c˜ao de
n vari´aveis:
µ(x1, . . . , xn) = x =
1
n
(x1 + x2 + . . . + xn)
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 2 / 55

3. Defini¸c˜ao
Seja D um conjunto do espa¸co n-dimensional (D ⊆ IRn
), isto ´e, os
elementos de D s˜ao os n-uplos ordenados (x1, x2, . . . , xn) de n´umeros
reais.
Se a cada ponto (x1, x2, . . . , xn) ∈ D fizermos corresponder um ´unico
elemento y ∈ IR, obtemos uma fun¸c˜ao
f : D ⊆ IRn
→ IR
(x1, x2, . . . , xn) → y = f (x1, x2, . . . , xn)
Esta fun¸c˜ao ´e chamada fun¸c˜ao real de n vari´aveis reais. O conjunto D ´e
denominado o dom´ınio da fun¸c˜ao.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 3 / 55

4. Representa¸c˜ao no plano e no espa¸co do dom´ınio de
fun¸c˜oes de duas e trˆes vari´aveis - Exemplos
Calcule o dom´ınio da fun¸c˜ao seguinte e represente-o graficamente:
f (x, y) = 3x2√
y − 1
Solu¸c˜ao
O dom´ınio de f ´e o conjunto
dos pontos (x, y) tais que
y ≥ 0.
Assim
D = {(x, y) ∈ IR2
: y ≥ 0}
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 4 / 55

5. Representa¸c˜ao no plano e no espa¸co do dom´ınio de
fun¸c˜oes de duas e trˆes vari´aveis - Exemplos (cont.)
Calcule o dom´ınio da fun¸c˜ao seguinte e represente-o graficamente:
f (x, y) = ln(x2 − y)
Solu¸c˜ao
O dom´ınio de f ´e o conjunto
dos pontos (x, y) tais que
x2 − y > 0.
Ora x2 − y > 0 ⇔ y < x2.
Assim
D = {(x, y) ∈ IR2
: y < x2
}
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 5 / 55

6. Representa¸c˜ao no plano e no espa¸co do dom´ınio de
fun¸c˜oes de duas e trˆes vari´aveis - Exemplos (cont.)
Calcule o dom´ınio da fun¸c˜ao seguinte e represente-o graficamente:
f (x, y) = 9 − x2 − y2 − z2
Solu¸c˜ao
O dom´ınio de f ´e o conjunto
dos pontos (x, y, z) tais que
9 − x2 − y2 − z2 ≥ 0.
Ora 9 − x2 − y2 − z2 ≥ 0 ⇔
x2 + y2 + z2 ≤ 9.
Assim
o dom´ınio de f ´e a esfera de raio
3 e centro em (0, 0, 0) e o seu
interior.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 6 / 55

7. Gr´aficos de fun¸c˜oes de duas vari´aveis
Se f ´e uma fun¸c˜ao de n vari´aveis, f = f (x1, x2, . . . , xn), o seu
gr´afico ´e o conjunto de pontos no espa¸co IRn+1
dado por
graf (f ) = {(x1, x2, . . . , xn, f (x1, x2, . . . , xn)) : (x1, x2, . . . , xn) ∈ D(f )}
Em particular seja f (x, y) uma fun¸c˜ao real de duas vari´aveis reais. O
gr´afico desta fun¸c˜ao definido por:
graf (f ) = {(x, y, f (x, y)) : (x, y) ∈ D(f )}
Nem toda a superf´ıcie em IR3
corresponde ao gr´afico de uma fun¸c˜ao.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 7 / 55

8. Gr´aficos de fun¸c˜oes de duas vari´aveis - Exemplos
f (x, y) = 1 − x −
1
2
y
f (x, y) = 1 − x2 − y2
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 8 / 55

9. Nota
Os gr´aficos de fun¸c˜oes de trˆes ou mais vari´aveis j´a n˜ao s˜ao visualiz´aveis por
se encontrar num espa¸co de dimens˜ao superior ao espa¸co onde vivemos.
Em IRn
, n ≥ 4, fun¸c˜oes cont´ınuas representam hiper-superf´ıcies.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 9 / 55

10. Curvas e Superf´ıcies de N´ıvel
Seja z = f (x, y) a equa¸c˜ao de uma superf´ıcie em IR3
correspondente ao
gr´afico de uma fun¸c˜ao.
Uma curva de n´ıvel na superf´ıcie ´e o lugar geom´etrico dos pontos
(x, y) ∈ D(f ) onde a fun¸c˜ao permanece constante e por isso ´e definida por
uma equa¸c˜ao f (x, y) = k , onde ´e k ´e uma constante.
Do ponto de vista geom´etrico as curvas de n´ıvel s˜ao as intersec¸c˜oes da
superf´ıcie z = f (x, y) com os planos horizontais z = k.
Para as fun¸c˜oes de trˆes vari´aveis o lugar geom´etrico dos pontos onde a
fun¸c˜ao ´e constante, definido por f (x, y, z) = k chama-se superf´ıcie de
n´ıvel e, para as fun¸c˜oes de mais de trˆes vari´aveis chama-se
hiper-superf´ıcie de n´ıvel.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 10 / 55

11. Curvas e Superf´ıcies de N´ıvel
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 11 / 55

12. Curvas e Superf´ıcies de N´ıvel - Exemplo 1
As figuras seguintes mostram uma montanha e a sua representa¸c˜ao
topogr´afica.
Geralmente os mapas de contorno ou cartas topogr´aficas mostram regi˜oes
da superf´ıcie terrestre descritas por curvas de n´ıvel, isto ´e, conjuntos de
pontos com a mesma eleva¸c˜ao.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 12 / 55

13. Curvas e Superf´ıcies de N´ıvel - Exemplo 1 - cont.
Uma carta topogr´afica descreve a varia¸c˜ao de z relativamente a x e a y do
seguinte modo:
se duas curvas de n´ıvel se encontram muito espa¸cadas significa que z varia
suavemente, enquanto que pequenos espa¸camentos mostram uma r´apida
altera¸c˜ao de z.
Desta maneira, para se obter uma boa ilus˜ao tridimensional numa carta
topogr´afica, ´e muito importante escolher valores adequados para k.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 13 / 55

14. Curvas e Superf´ıcies de N´ıvel - Exemplo 2
Nas cartas meteorol´ogicas as curvas de n´ıvel podem representar pontos de
igual temperatura, e chamam-se isot´ermicas. Podem tamb´em representar
pontos de igual press˜ao, curvas isob´aricas, como se mostra na figura
abaixo.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 14 / 55

15. Curvas e Superf´ıcies de N´ıvel - Exemplo 3
Considere a fun¸c˜ao dada por f (x, y) = 4x2 + y2. Construa o mapa de
contorno para esta superf´ıcie atrav´es das curvas de n´ıvel correspondentes a
k = 0, 1, 2, 3, 4 e 5.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 15 / 55

16. Curvas e Superf´ıcies de N´ıvel - Exemplo 4
Considere a fun¸c˜ao dada por f (x, y) = 2 − x − y. Construa o mapa de
contorno para esta superf´ıcie atrav´es das curvas de n´ıvel correspondentes a
k = −6, −4, 0, 2, 4 e 6.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 16 / 55

17. Esbo¸co de gr´aficos usando curvas de n´ıvel
As curvas de n´ıvel s˜ao sempre subconjuntos do dom´ınio da fun¸c˜ao
z = f (x, y), e portanto s˜ao tra¸cadas no plano XOY .
Cada curva de n´ıvel ´e a projec¸c˜ao, sobre o plano XOY da intersec¸c˜ao do
gr´afico de f com o plano horizontal z = k.
Assim, para obtermos uma visualiza¸c˜ao do gr´afico de f , podemos tra¸car
diversas curvas de n´ıvel e imaginarmos cada uma dessas curvas deslocada
para a altura z = k correspondente.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 17 / 55

18. Esbo¸co de gr´aficos usando curvas de n´ıvel - Ilustra¸c˜ao
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 18 / 55

19. Sec¸c˜oes C´onicas
As sec¸c˜oes c´onicas, ou simplesmente as c´onicas, s˜ao obtidas interceptando
um cone circular recto de duas folhas por um plano
Variando a posi¸c˜ao do plano
obtˆem-se uma par´abola, uma
elipse ou uma hip´erbole como ilus-
tra a figura ao lado:
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 19 / 55

20. Uma par´abola ´e o conjunto de todos os pontos de um plano equidistantes
de um ponto fixo F (foco) e de uma recta fixa l (directriz) do plano.
O eixo da par´abola ´e a recta que passa por F e ´e perpendicular `a directriz.
O v´ertice da par´abola ´e o ponto V do eixo, equidistante de F e l
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 20 / 55

21. Par´abolas com v´ertice no ponto V=(h,k)
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 21 / 55

22. Uma elipse ´e o conjunto de todos os pontos de um plano, cuja soma das
distˆancias a dois pontos fixos (focos) ´e constante.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 22 / 55

23. O gr´afico da equa¸c˜ao
x2
a2
+
y2
b2
= 1
com a2 > b2 ´e uma elipse com v´ertices (±a, 0). As extremidades do eixo
menor s˜ao (0, ±b). Os focos s˜ao (±c, 0), com c2 = a2 − b2.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 23 / 55

24. O gr´afico da equa¸c˜ao
x2
b2
+
y2
a2
= 1
com a2 > b2 ´e uma elipse com v´ertices (0, ±a). As extremidades do eixo
menor s˜ao (±b, 0). Os focos s˜ao (0, ±c), com c2 = a2 − b2.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 24 / 55

25. Uma hip´erbole ´e o conjunto de todos os pontos de um plano, tais que o
m´odulo da diferen¸ca das suas distˆancias a dois pontos fixos do plano (os
focos) ´e constante.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 25 / 55

26. O gr´afico da equa¸c˜ao
x2
a2
−
y2
b2
= 1
com a2 > b2 ´e uma hip´erbole de v´ertices (±a, 0). Os focos s˜ao (±c, 0),
com c2 = a2 + b2.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 26 / 55

27. O gr´afico da equa¸c˜ao
y2
a2
−
x2
b2
= 1
com a2 > b2 ´e uma hip´erbole de v´ertices (0, ±a). Os focos s˜ao (0, ±c),
com c2 = a2 + b2.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 27 / 55

28. Planos
A equa¸c˜ao de um plano no espa¸co pode ser obtida atrav´es de um ponto
do plano e um vector normal a esse plano.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 28 / 55

29. Defini¸c˜ao
O plano contendo o ponto (x1, y1, z1) e o vector normal −→n = (a, b, c),
pode ser representado, pela equa¸c˜ao
a(x − x1) + b(y − y1) + c(z − z1) = 0
ou ainda, reagrupando os termos, obt´em-se para equa¸c˜ao geral do plano:
ax + by + cz + d = 0, d ∈ IR
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 29 / 55

30. Exemplo
Encontre a equa¸c˜ao geral do plano que cont´em o ponto (1, 2, 3) e sendo
−→n = (4, 5, 6) um vector normal ao plano
Solu¸c˜ao:
4(x − 1) + 5(y − 2) + 6(z − 3) = 0
4x + 5y + 6z − 32 = 0
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 30 / 55

31. Para esbo¸car um plano no espa¸co, devemos em primeiro lugar encontrar as
rectas de intersec¸c˜ao com os planos coordenados:
XOY (z = 0);
YOZ (x = 0);
XOZ (y = 0)
e as intersec¸c˜oes com planos paralelos aos planos coordenados.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 31 / 55

32. Exemplo
Pegando na equa¸c˜ao do exemplo anterior vem:
Fazendo z = 0 vem 4x + 5y = 32
Fazendo x = 0 vem 5y + 6z = 32
Fazendo y = 0 vem 4x + 6z = 32
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 32 / 55

33. Defini¸c˜ao
A intersec¸c˜ao de uma superf´ıcie com um plano diz-se o tra¸co da superf´ıcie
no plano.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 33 / 55

34. Superf´ıcies Cil´ındricas
Um exemplo comum de uma
destas superf´ıcies ´e o cilindro
circular recto.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 34 / 55

35. Para desenhar o gr´afico de z = y2 em IR3
come¸camos por calcular o tra¸co
(i.e., o que representa a fun¸c˜ao para diferentes valores de x) desta
superf´ıcie com os planos paralelos ao plano YOZ, uma vez que a vari´avel x
n˜ao est´a presente na equa¸c˜ao. O tra¸co em cada um destes planos ´e a
par´abola z = y2.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 35 / 55

36. Outro tipo de superf´ıcies no espa¸co s˜ao as superf´ıcies qu´adricas que
podem ser consideradas a correspondˆencia tridimensional das sec¸c˜oes
c´onicas no plano.
Defini¸c˜ao
Uma superf´ıcie qu´adrica ´e representada por uma equa¸c˜ao do segundo grau
da forma:
Ax2
+ By2
+ Cz2
+ Dxz + Exy + Fyz + Gx + Hy + Iz + J = 0
A intersec¸c˜ao de uma superf´ıcie com um plano diz-se o tra¸co da superf´ıcie
no plano.
Os tra¸cos das superf´ıcies qu´adricas nos planos coordenados s˜ao c´onicas.
Para visualizar uma superf´ıcie no espa¸co ´e ´util determinar os seus tra¸cos
em planos paralelos aos planos coordenados.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 36 / 55

37. H´a seis tipos b´asicos de superf´ıcies qu´adricas:
1 Elips´oide
2 Hiperbol´oide de uma folha
3 Hiperbol´oide de duas folhas
4 Cone el´ıptico
5 Parabol´oide el´ıptico
6 Parabol´oide hiperb´olico
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 37 / 55

38. Elips´oide
x2
a2 + y2
b2 + z2
c2 = 1
Os tra¸cos nos planos
coordenados s˜ao elipses. A
superf´ıcie ´e uma esfera se
a = b = c = 0.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 38 / 55

39. Hiperbol´oide de uma folha
x2
a2 + y2
b2 − z2
c2 = 1
O tra¸co nos planos paralelos
ao plano XOY s˜ao elipses e
nos planos paralelos aos outros
planos coordenados o tra¸co ´e
uma hip´erboles.O eixo do
hiperbol´oide corresponde `a
vari´avel cujo coeficiente ´e
negativo.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 39 / 55

40. Hiperbol´oide de duas folhas
z2
c2 − x2
a2 − y2
b2 = 1
O tra¸co nos planos paralelos
ao plano XOY s˜ao elipses e
nos planos paralelos aos outros
planos coordenados o tra¸co ´e
uma hip´erbole. O eixo do
hiperbol´oide corresponde `a
vari´avel cujo coeficiente ´e
positivo. N˜ao h´a tra¸co no
plano coordenado
perpendicular a esse eixo.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 40 / 55

41. Cone El´ıptico
z2 = x2
a2 + y2
b2
O tra¸co nos planos paralelos
ao plano XOY s˜ao elipses e
nos planos paralelos aos outros
planos coordenados o tra¸co ´e
uma recta. O eixo do cone
corresponde `a vari´avel cujo
coeficiente ´e negativo.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 41 / 55

42. Parabol´oide El´ıptico
z = x2
a2 + y2
b2
O tra¸co nos planos paralelos
ao plano XOY s˜ao elipses e
nos planos paralelos aos outros
planos coordenados o tra¸co ´e
uma par´abola. O eixo do
parabol´oide corresponde `a
vari´avel de grau um.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 42 / 55

43. Parabol´oide Hiperb´olico
z = y2
b2 − x2
a2
O tra¸co nos planos paralelos
ao plano XOY s˜ao hip´erboles e
nos planos paralelos aos outros
planos coordenados o tra¸co ´e
uma par´abola. O eixo do
parabol´oide corresponde `a
vari´avel de grau um.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 43 / 55

44. T´ecnica para identificar uma superf´ıcie qu´adrica
Equa¸c˜ao Caracter´ıstica Classifica¸c˜ao
x2
a2
+
y2
b2
+
z2
c2
= 1 N˜ao tem nenhum sinal menos Elips´oide
x2
a2
+
y2
b2
−
z2
c2
= 1 Tem apenas um sinal menos Hiperbol´oide de uma folha
z2
c2
−
x2
a2
−
y2
b2
= 1 Tem dois sinais menos Hiperbol´oide de duas folhas
z2
−
x2
a2
−
y2
b2
= 0 N˜ao tem termos lineares Cone El´ıptico
z −
x2
a2
−
y2
b2
= 0
Tem um termo linear e dois
termos quadr´aticos Parabol´oide El´ıptico
com o mesmo sinal
z −
y2
b2
+
x2
a2
= 0
Tem um termo linear e dois
termos quadr´aticos Parabol´oide Hiperb´olico
com sinais contr´arios
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 44 / 55

45. Exemplo
Identifique a seguinte superf´ıcie:
3x2
− 4y2
+ 12z2
+ 12 = 0
Solu¸c˜ao:
Reescrevendo a equa¸c˜ao vem:
y2
3
−
x2
4
− z2
= 1
A equa¸c˜ao tem um 1 no lado direito da equa¸c˜ao, tem dois membros com
sinal negativo no lado esquerdo e um positivo e por isso ´e um hiperbol´oide
de duas folhas.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 45 / 55

46. Esbo¸co de qu´adricas... Algumas t´ecnicas e exemplos
Um esbo¸co de um hiperbol´oide de uma folha de equa¸c˜ao
x2
a2
+
y2
b2
−
z2
c2
= 1 (a > 0, b > 0, c > 0)
pode ser obtida desenhando primeiro o tra¸co (elipse) no plano XOY,
depois os tra¸cos nos planos z = ±c, e por fim as curvas hiperb´olicas que
unem os pontos terminais dos eixos dessas elipses.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 46 / 55

47. Exemplo
Esboce o gr´afico do hiperbol´oide de uma folha de equa¸c˜ao
x2
+ y2
−
z2
4
= 1 .
O tra¸co no plano XOY, obtido fazendo z = 0 na equa¸c˜ao, ´e
x2
+ y2
= 1 (z = 0)
que ´e uma circunferˆencia de raio 1 e centro na origem.
Os tra¸cos nos planos z = 2 e z = −2 s˜ao
x2
+ y2
= 2
que s˜ao c´ırculos de raio
√
2 e centro no eixo dos zz. Juntando os pontos
extremos dos eixos das circunferˆencias com hip´erboles obtemos o esbo¸co
final que se encontra no slide seguinte
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 47 / 55

48. O esbo¸co...
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 48 / 55

49. Um esbo¸co de um hiperbol´oide de duas folhas de equa¸c˜ao
z2
c2
−
x2
a2
−
y2
b2
= 1 (a > 0, b > 0, c > 0)
pode ser obtida desenhando primeiro as intersec¸c˜oes com o eixo dos zz,
depois os tra¸cos (elipses) nos planos z = ±2c, e por fim as curvas que
unem os pontos terminais dos eixos dessas elipses com os pontos da
intersec¸c˜ao com o eixo dos zz.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 49 / 55

50. Exemplo
Esboce o gr´afico do hiperbol´oide de duas folhas de equa¸c˜ao
z2
− x2
−
y2
4
= 1 .
As intersec¸c˜oes com o eixo dos zz acontecem em z = ±1. Os tra¸cos nos
planos z = 2 e z = −2 s˜ao dados pela equa¸c˜ao:
x2
3
+
y2
12
= 1 (z = ±2)
Desenhando estas elipses e as hip´erboles nos planos coordenados verticais
obtemos o esbo¸co do slide seguinte
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 50 / 55

51. O esbo¸co...
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 51 / 55

52. Um esbo¸co de um parabol´oide hiperb´olico de equa¸c˜ao
z =
y2
b2
−
x2
a2
(a > 0, b > 0)
pode ser obtida desenhando primeiro os dois tra¸cos ( par´abolas ) que
passam na origem ( um no plano YOZ e outra no plano XOZ ), depois os
tra¸cos (hip´erboles) nos planos z = ±1, e por fim preencher os lados que
faltam.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 52 / 55

53. Exemplo
Esboce o gr´afico do parabol´oide hiperb´olico de equa¸c˜ao
z =
y2
4
−
x2
9
Fazendo x = 0 na equa¸c˜ao vem:
z =
y2
4
(x = 0)
que ´e uma par´abola no plano YOZ com v´ertice na origem e a “abrir”para
o lado positivo do eixo dos zz. Fazendo y = 0 na equa¸c˜ao vem:
z = −
x2
4
(y = 0)
que ´e uma par´abola no plano XOZ com v´ertice na origem e a “abrir”para
o lado negativo do eixo dos zz.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 53 / 55

54. O tra¸co no plano z = 1 ´e
y2
4
−
x2
9
= 1 (z = 1)
que ´e uma hip´erbole que “abre”ao longo de uma linha paralela ao eixo dos
yy. O tra¸co no plano z = −1 ´e
x2
9
−
y2
4
= 1 (z = −1)
que ´e uma hip´erbole que “abre”ao longo de uma linha paralela ao eixo dos
xx.
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 54 / 55

55. O esbo¸co...
Nuno Bastos (ESTGV) M´etodos Matem´aticos II 2014/2015 55 / 55