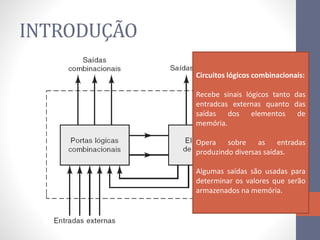
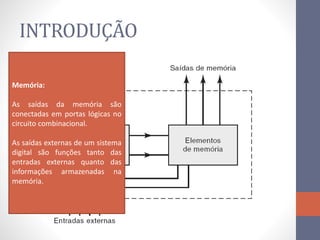
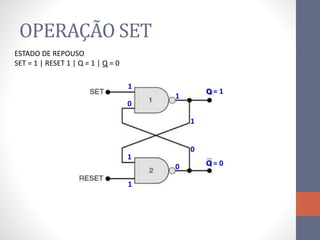
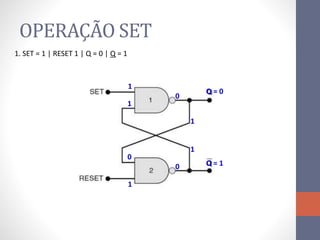
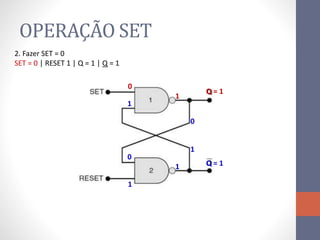
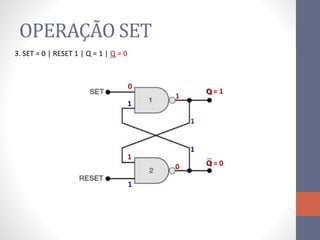
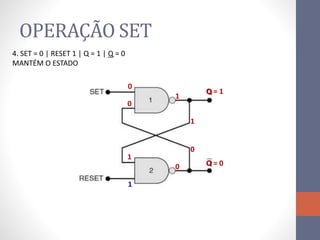
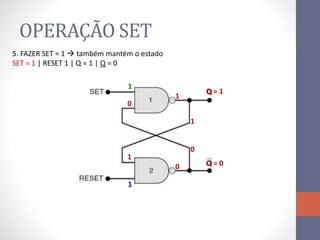
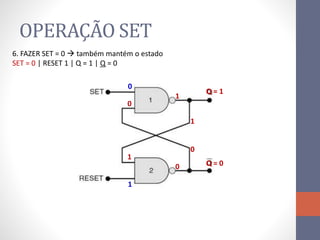
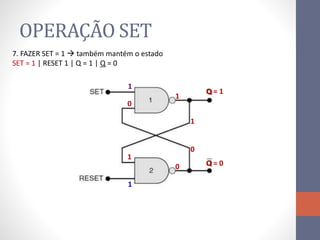
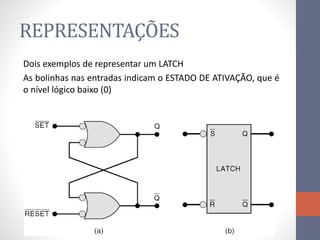
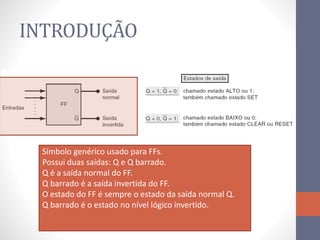
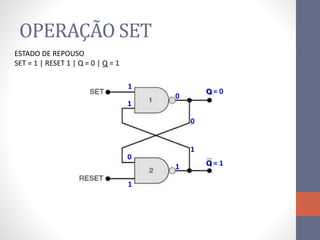
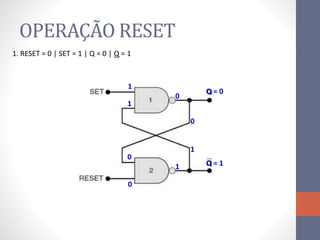
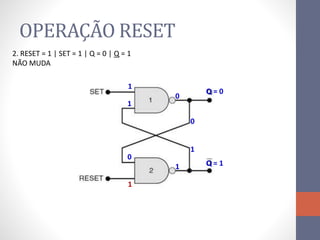
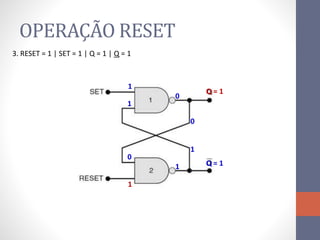
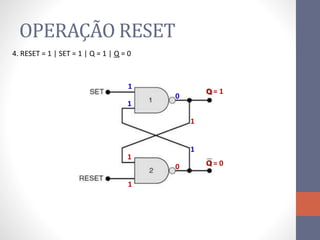
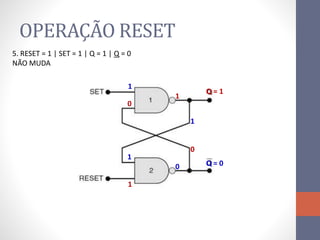
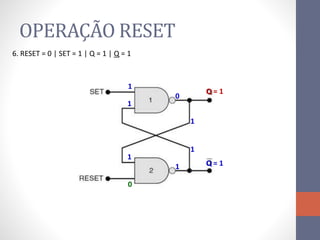
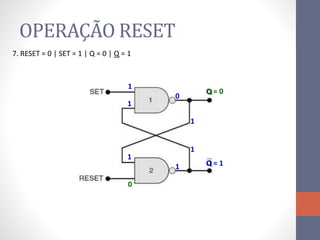
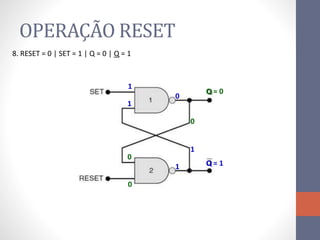
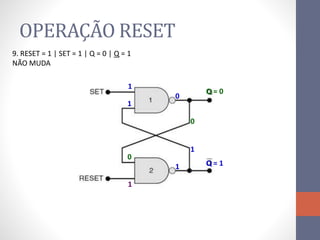
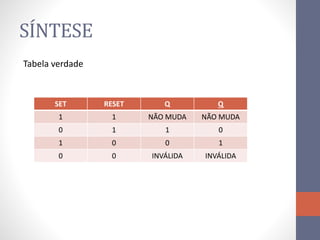
O documento descreve os conceitos básicos de circuitos lógicos digitais, incluindo: 1) Circuitos combinacionais cujas saídas dependem apenas das entradas atuais, sem memória. 2) Elementos de memória como flip-flops (FF) que armazenam estado usando realimentação. 3) Um circuito FF básico usando portas NAND com entradas SET e RESET para alternar os estados de saída Q e Q barrado.

1. FLIP FLOPS – Parte 1
CIRCUITOS DIGITAIS
CIÊNCIA DA COMPUTAÇÃO
UNIVERSIDADE DO SAGRADO CORAÇÃO

2. INTRODUÇÃO
• Circuitos lógicos combinacionais:
• Níveis lógicos de saída dependem apenas dos níveis
lógicos presentes nas entradas
• Nenhuma condição de entrada anterior tem efeito sobre
as saídas atuais
• Não possui memória
• SISTEMAS DIGITAIS:
• Compostos de circuitos lógicos combinacionais e
circuitos de memória

3. INTRODUÇÃO
Circuitos lógicos combinacionais:
Recebe sinais lógicos tanto das
entradcas externas quanto das
saídas dos elementos de
memória.
Opera sobre as entradas
produzindo diversas saídas.
Algumas saídas são usadas para
determinar os valores que serão
armazenados na memória.

4. INTRODUÇÃO
Memória:
As saídas da memória são
conectadas em portas lógicas no
circuito combinacional.
As saídas externas de um sistema
digital são funções tanto das
entradas externas quanto das
informações armazenadas na
memória.

5. INTRODUÇÃO
• FLIP-FLOP: elemento de memória mais importante em um
sistema digital.
• Uma porta lógica não consegue armazenar nada, mas várias
portas lógicas podem ser conectadas de forma a conseguir
isto.
• REALIMENTAÇÃO: saídas das portas lógicas são conectadas de
volta à entradas de forma apropriada.

6. INTRODUÇÃO
Símbolo genérico usado para FFs.
Possui duas saídas: Q e Q barrado.
Q é a saída normal do FF.
Q barrado é a saída invertida do FF.
O estado do FF é sempre o estado da saída normal Q.
Q barrado é o estado no nível lógico invertido.

7. INTRODUÇÃO
 Um FF pode ter uma ou mais entradas usadas para fazer com que o FF
comute entre os possíveis estados de saída.
 A maioria das entradas do FF precisa ser apenas momentaneamente
ativada (ou pulsada) para provocar a mudança de estado na saída do FF.
 A saída permanece no novo estado mesmo após o pulso de entrada
terminar (mantém o estado - memória)
 FF também é conhecido como LATCH ou MULTIVIBRADOR BIESTÁVEL.

8. LATCH COM PORTAS NAND
• Entradas são ativas em nível BAIXO.
• As saídas mudarão quando as entradas forem pulsadas para
BAIXO.
• O latch da porta NAND ou simplesmente latch é um FF
básico.
Entradas são SET e CLEAR (RESET):
• (a) Quando o latch é setado: Q = 1 e Q = 0
• (b) Quando o latch é limpo ou resetado: Q = 0 e Q = 1
• As entradas SET e RESET estão em repouso no estado
ALTO
• Uma delas é pulsada em nível baixo sempre que é
necessário alterar as saídas

9. LATCH COM PORTAS NAND
ANALISANDO O CIRCUITO
Entradas: SET = RESET = 1
Saídas: Q = 0 e Q = 1
 As entradas da NAND 2 são 0 e 1
 Portanto, Q = 1
 Q faz com que a NAND 1 tenha nível 1
em ambas as entradas para gerar 0 na
saída Q
 Portanto, nível baixo na saída da NAND
1 que gera um nível alto na saída a
NAND 2 que, por sua vez, MANTÉM a
saída da NAND 1 em nível baixo

10. LATCH COM PORTAS NAND
ANALISANDO O CIRCUITO
Entradas: SET = RESET = 1
Saídas: Q = 1 e Q = 0
 Nível alto na saída da NAND 1 gera
nível baixo na saída da NAND 2, que,
por sua vez, MANTÉM a saída da
NAND 1 em nível alto.
CONCLUINDO:
Quando SET = RESET = 1 DOIS estados de
saída são possíveis para o FF
O estado ATUAL da saída do FF depende
sempre do que aconteceu anteriormente
nas entradas.

11. OPERAÇÃO SET
1
1
1
Q = 0
0
0
1
Q = 1
0
1
ESTADO DE REPOUSO
SET = 1 | RESET 1 | Q = 0 | Q = 1

12. OPERAÇÃO SET
1
1
0
Q = 1
1
1
0
Q = 0
1
0
ESTADO DE REPOUSO
SET = 1 | RESET 1 | Q = 1 | Q = 0

13. OPERAÇÃO SET
1
1
1
Q = 0
1
0
1
Q = 1
0
0
1. SET = 1 | RESET 1 | Q = 0 | Q = 1

14. OPERAÇÃO SET
0
1
1
Q = 1
0
0
1
Q = 1
1
1
2. Fazer SET = 0
SET = 0 | RESET 1 | Q = 1 | Q = 1

15. OPERAÇÃO SET
0
1
1
Q = 1
1
1
1
Q = 0
1
0
3. SET = 0 | RESET 1 | Q = 1 | Q = 0

16. OPERAÇÃO SET
0
1
0
Q = 1
1
1
0
Q = 0
1
0
4. SET = 0 | RESET 1 | Q = 1 | Q = 0
MANTÉM O ESTADO

17. OPERAÇÃO SET
1
1
0
Q = 1
1
1
0
Q = 0
1
0
5. FAZER SET = 1  também mantém o estado
SET = 1 | RESET 1 | Q = 1 | Q = 0

18. OPERAÇÃO SET
0
1
0
Q = 1
1
1
0
Q = 0
1
0
6. FAZER SET = 0  também mantém o estado
SET = 0 | RESET 1 | Q = 1 | Q = 0

19. OPERAÇÃO SET
1
1
0
Q = 1
1
1
0
Q = 0
1
0
7. FAZER SET = 1  também mantém o estado
SET = 1 | RESET 1 | Q = 1 | Q = 0

20. OPERAÇÃO RESET
1
0
1
Q = 0
0
0
1
Q = 1
0
1
1. RESET = 0 | SET = 1 | Q = 0 | Q = 1

21. OPERAÇÃO RESET
1
1
1
Q = 0
0
0
1
Q = 1
0
1
2. RESET = 1 | SET = 1 | Q = 0 | Q = 1
NÃO MUDA

22. OPERAÇÃO RESET
1
1
1
Q = 1
0
0
1
Q = 1
0
1
3. RESET = 1 | SET = 1 | Q = 1 | Q = 1

23. OPERAÇÃO RESET
1
1
1
Q = 1
1
1
1
Q = 0
0
0
4. RESET = 1 | SET = 1 | Q = 1 | Q = 0

24. OPERAÇÃO RESET
1
1
0
Q = 1
1
1
0
Q = 0
1
0
5. RESET = 1 | SET = 1 | Q = 1 | Q = 0
NÃO MUDA

25. OPERAÇÃO RESET
1
0
1
Q = 1
1
1
1
Q = 1
0
1
6. RESET = 0 | SET = 1 | Q = 1 | Q = 1

26. OPERAÇÃO RESET
1
0
1
Q = 0
1
1
1
Q = 1
0
1
7. RESET = 0 | SET = 1 | Q = 0 | Q = 1

27. OPERAÇÃO RESET
1
0
1
Q = 0
0
0
1
Q = 1
0
1
8. RESET = 0 | SET = 1 | Q = 0 | Q = 1

28. OPERAÇÃO RESET
1
1
1
Q = 0
0
0
1
Q = 1
0
1
9. RESET = 1 | SET = 1 | Q = 0 | Q = 1
NÃO MUDA

29. SETAR E RESETAR
• Quando SET = 0 e RESET = 0, as saídas no circuito serão Q = 1 e
Q = 1, que é considerado um estado indesejável
• As saídas devem ser complementares, portanto, NUNCA
devem ter o mesmo nível lógico
• Transições SIMULTANEAS de volta para o nível lógico 1
produzirão resultados IMPREVISÍVEIS
• O estado resultante da saída sempre dependerá da entrada
(set ou reset) que retornou primeiro para o nível alto

30. SÍNTESE
1. SET = RESET = 1
Estado normal de repouso
Não tem efeito sobre o estado da saída
Q e Q permanecem no mesmo estado lógico qu estavam
antes desta condição de entrada
2. SET = 0, RESET = 1
Q sempre vai para 1
Q permanecerá neste estado lógico mesmo que SET saia
de zero e vá para 1.
Operação SET

31. SÍNTESE
3. SET = 1, RESET = 0
Q sempre vai para 0
Q permanece em 0 mesmo que RESET saia de 0 e vá
para 1
Operação RESET
4. SET = RESET = 0
Produz Q = Q = 1
O resultado é imprevisível caso as entradas (set e reset)
saiam de 0 e voltem para 1

32. SÍNTESE
Tabela verdade
SET RESET Q Q
1 1 NÃO MUDA NÃO MUDA
0 1 1 0
1 0 0 1
0 0 INVÁLIDA INVÁLIDA

33. REPRESENTAÇÕES
Dois exemplos de representar um LATCH
As bolinhas nas entradas indicam o ESTADO DE ATIVAÇÃO, que é
o nível lógico baixo (0)

34. EXERCÍCIOS