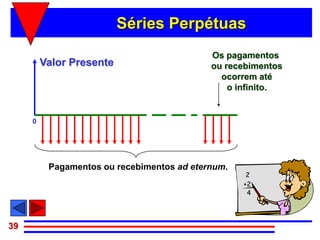
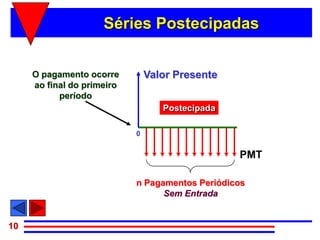
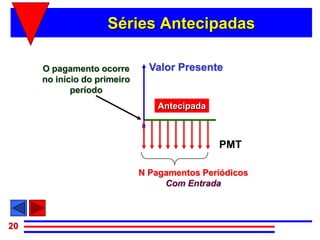
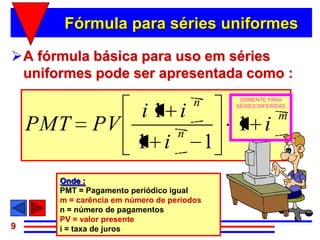
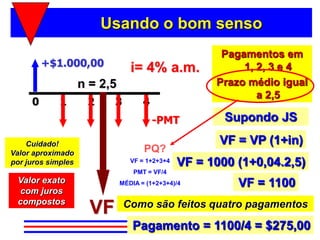
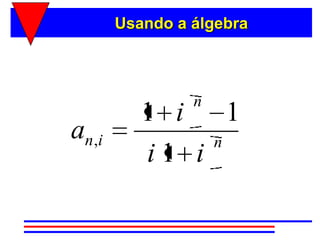
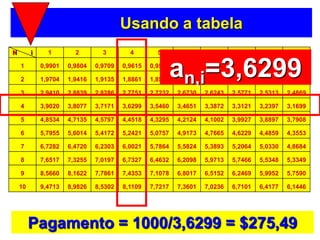
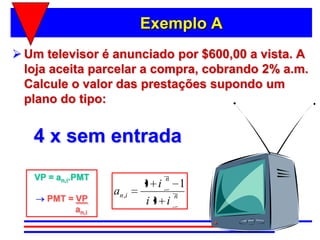
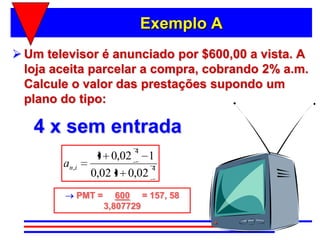
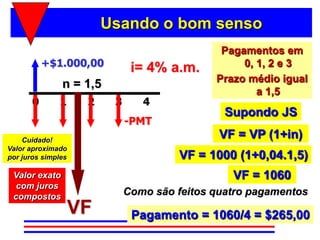
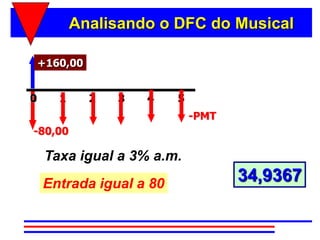
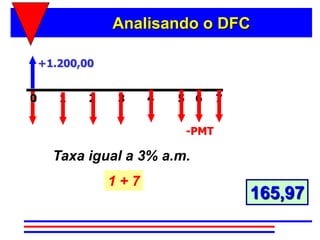
1) O documento discute séries uniformes, que são sequências de pagamentos ou recebimentos com valores iguais. 2) Séries uniformes podem ser classificadas como antecipadas, postecipadas ou diferidas dependendo do momento em que os pagamentos ocorrem. 3) A fórmula básica para cálculo de séries uniformes é apresentada, permitindo calcular o valor presente ou as prestações a partir dos demais parâmetros.

1. Séries Uniformes
Operações
com Séries
Uniformes
1

2. Séries Uniformes
Objetivos :
– Entender o DFC em séries
– Diferenciar séries antecipadas,
postecipadas e diferidas
– Compreender os cálculos
envolvendo séries uniformes
– Discutir os principais
aspectos associados às
séries uniformes
2

3. Conceito de Séries
Seqüência de pagamentos ou
recebimentos em datas futuras,
como contrapartida de recebimento
ou aplicação a valor presente

4. Classificações de Séries
Quanto ao Finitas : quando ocorrem durante um período pré-determinado de tempo
número de
prestações: Infinitas : ou perpetuidades, ocorrem quando ocorrem de forma ad eternum. Isto
é, quando os pagamentos ou recebimentos duram de forma infinita.
Quanto à Periódicas : quando os pagamentos ocorrem a intervalos constantes
periodicidade dos
pagamentos: Não-periódicas : quando os pagamentos ou recebimentos acontecem em
intervalos irregulares de tempo
Quanto ao valor Uniformes : quando as prestações ou anuidades são iguais.
das prestações:
Não-uniformes : quando os pagamentos ou recebimentos apresentam valores
distintos
Quanto ao prazo Postecipadas : quando as anuidades iniciam após o final do primeiro período
dos pagamentos:
Antecipadas : quando o primeiro pagamento ocorre na entrada, do início da série
Quanto ao Diferidas : ou com carência, quando houver um prazo maior que um período entre
primeiro a data do recebimento do financiamento e data de pagamento da primeira
pagamento: prestação
Não diferidas : quando não existir prazo superior a um período entre o início da
operação e o primeiro pagamento ou recebimento.
4

5. Tipos de séries
 Uniformes
– Valores nominais iguais
 Não uniformes
– Valores nominais diferentes
Esta aula:
Séries Uniformes

6. Classificação das séries
 Antecipadas
– Com entrada
– Exemplos … 1 + 2, 1 + 5, 1 + …
 Postecipadas
– Sem entrada
– Exemplos … 2x, 5x, 6x …

7. Conceito de Séries Uniformes
 Consistem em uma sequência de recebimentos
ou pagamentos, cujos valores são iguais.
 Genericamente, as séries uniformes podem ser
representadas de acordo com a figura a seguir:
7

8. DFC genérico de série uniforme
VP = Valor Presente
n = número de pagamentos iguais
Carência
m +1
0
PMT = Prestações ou Pagamentos
8

9. Séries Uniformes
Fórmula para séries uniformes
A fórmula básica para uso em séries
uniformes pode ser apresentada como :
n SOMENTE PARA
i1 i SÉRIES DIFERIDAS
m
PMT PV n
1 i
1 i 1
Onde :
PMT = Pagamento periódico igual
m = carência em número de períodos
n = número de pagamentos
PV = valor presente
9 i = taxa de juros

10. Séries Postecipadas
O pagamento ocorre Valor Presente
ao final do primeiro
período
Postecipada
0
PMT
n Pagamentos Periódicos
Sem Entrada
10

11. A geladeira nova de Pedro
Valores nominais
 Pedro quer comprar uma
iguais
geladeira
 Na loja, $1.000,00 a vista Séries
UNIFORMES
 Ou … em quatro iguais mensais,
sem entrada Como obter
PMT?
+$1.000,00 Álgebra
Tabelas
HP 12C
0 1 2 3 4
-PMT Taxa da loja?
i= 4% a.m.

12. Usando o bom senso
Pagamentos em
+$1.000,00 i= 4% a.m. 1, 2, 3 e 4
n = 2,5 Prazo médio igual
a 2,5
0 1 2 3 4
-PMT Supondo JS
Cuidado! VF = VP (1+in)
Valor aproximado PQ?
por juros simples VF = 1+2+3+4 VF = 1000 (1+0,04.2,5)
PMT = VF/4
Valor exato MÉDIA = (1+2+3+4)/4 VF = 1100
com juros
compostos
VF Como são feitos quatro pagamentos
Pagamento = 1100/4 = $275,00

13. Séries Postecipadas
13

14. Utilizando an’i
VP = an,i.PMT
PMT = VP
an,i

15. Usando a álgebra
n
1 i 1
an , i n
i1 i

16. Usando a tabela
N i 1 2 3 4 5 6 7 8 9 10
1
2
0,9901
1,9704
0,9804
1,9416
0,9709
1,9135
0,9615
1,8861
0,9524
1,8594
an,i=3,6299
0,9434
1,8334
0,9346
1,8080
0,9259
1,7833
0,9174
1,7591
0,9091
1,7355
3 2,9410 2,8839 2,8286 2,7751 2,7232 2,6730 2,6243 2,5771 2,5313 2,4869
4 3,9020 3,8077 3,7171 3,6299 3,5460 3,4651 3,3872 3,3121 3,2397 3,1699
5 4,8534 4,7135 4,5797 4,4518 4,3295 4,2124 4,1002 3,9927 3,8897 3,7908
6 5,7955 5,6014 5,4172 5,2421 5,0757 4,9173 4,7665 4,6229 4,4859 4,3553
7 6,7282 6,4720 6,2303 6,0021 5,7864 5,5824 5,3893 5,2064 5,0330 4,8684
8 7,6517 7,3255 7,0197 6,7327 6,4632 6,2098 5,9713 5,7466 5,5348 5,3349
9 8,5660 8,1622 7,7861 7,4353 7,1078 6,8017 6,5152 6,2469 5,9952 5,7590
10 9,4713 8,9826 8,5302 8,1109 7,7217 7,3601 7,0236 6,7101 6,4177 6,1446
Pagamento = 1000/3,6299 = $275,49

17. Exemplo A
 Um televisor é anunciado por $600,00 a vista. A
loja aceita parcelar a compra, cobrando 2% a.m.
Calcule o valor das prestações supondo um
plano do tipo:
4 x sem entrada
VP = an,i.PMT n
1 i 1
an , i n
PMT = VP i1 i
an,i

18. Exemplo A
 Um televisor é anunciado por $600,00 a vista. A
loja aceita parcelar a compra, cobrando 2% a.m.
Calcule o valor das prestações supondo um
plano do tipo:
4 x sem entrada
4
1 0,02 1
an , i 4
0,02 1 0,02
PMT = 600 = 157, 58
3,807729

19. E se os pagamentos fossem …
Com entrada
…

20. Séries Antecipadas
O pagamento ocorre Valor Presente
no início do primeiro
período
Antecipada
0
PMT
N Pagamentos Periódicos
Com Entrada
20

21. Usando o bom senso
Pagamentos em
+$1.000,00 i= 4% a.m. 0, 1, 2 e 3
Prazo médio igual
n = 1,5
a 1,5
0 1 2 3 4
Supondo JS
-PMT
Cuidado!
VF = VP (1+in)
Valor aproximado
por juros simples VF = 1000 (1+0,04.1,5)
Valor exato VF = 1060
com juros
compostos
Como são feitos quatro pagamentos
VF Pagamento = 1060/4 = $265,00

22. Séries Antecipadas
n
1 i 1
an , i n
i1 i
22

23. A geladeira nova de Pedro
 Pedro quer comprar uma
geladeira
 Na loja, $1.000,00 a vista
 Ou … em quatro iguais mensais,
com entrada
+$1.000,00 i= 4% a.m.
0 1 2 3 4
-PMT $264,89
JC = $265,00, diferença de $0,11!!!

24. Exemplo B
 Um televisor é anunciado por $600,00 a vista. A
loja aceita parcelar a compra, cobrando 2% a.m.
Calcule o valor das prestações supondo um
plano do tipo:
1+3x

25. Analisando o DFC: 4x
+600,00
0 1 2 3 4
-PMT
Taxa igual a 2% a.m.
Com entrada 154,4846

26. Exemplo C
 A Mercantil Precinho e Descontão
Ltda. pensa em financiar suas
vendas, cobrando uma taxa
composta mensal sempre igual a
3% a.m. Calcule o valor das
prestações nas operações de
venda financiada apresentadas
a seguir:

27. a) Rádio Somzão
Valor a vista igual a $400,00, em três iguais,
sem entrada.

28. Analisando o DFC do Somzão
+400,00
0 1 2 3 4
-PMT
Taxa igual a 3% a.m.
Sem entrada 141,4121

29. b) Tocador de CD Musical
Valor a vista igual a $240,00, entrada de
$80,00 mais cinco mensais iguais.

30. Analisando o DFC do Musical
+160,00
+240,00
0 1 2 3 4 5
-PMT
-80,00
Taxa igual a 3% a.m.
Entrada igual a 80
34,9367

31. c) Televisor Veja Mais
Valor a vista igual a $1.200,00, em 1 + 7.

32. Analisando o DFC
+1.200,00
0 1 2 3 4 5 6 7
-PMT
Taxa igual a 3% a.m.
1+7
165,97

33. d) Refrigerador Esquimó
Valor a vista igual a $2.100,00, em 1 + 3.

34. Analisando o DFC do Esquimó
+2.100,00
0 1 2 3
-PMT
Taxa igual a 3% a.m.
548,5017
1+3

35. Exercício de Fixação
 Uma máquina de cortar grama é
anunciada por $600,00 a vista ou
em 4 parcelas mensais iguais, sem
entrada. Se a taxa de juros
cobrada pela loja é igual a 2% ao
mês, qual o valor das prestações?
A 157 B 167 C 177 D 187 E 197
35

36. Exercício de Fixação
Um automóvel novo é vendido a vista por
$40.000,00 ou em dez parcelas mensais
iguais sem entrada no valor de $5.180,18.
Qual o valor da taxa de juros efetiva
mensal % da operação?
A 5 B 6 C 7 D 8 E 9
36

37. Exercício de Fixação
Um microcomputador é
anunciado por $1.200,00 a
vista ou em 9 parcelas
mensais iguais, com entrada.
Se a taxa de juros cobrada
pela loja é igual a 1% ao mês,
qual o valor das prestações?
A 109 B 119 C 129 D 139 E 149
37

38. Exercício de Fixação
Uma rede de lojas de
brinquedos anuncia a venda
de um robozinho eletrônico
por $300,00 a vista ou em (1+4)
prestações mensais iguais no
valor de $100,00. Qual a taxa
de juros da operação?
A 34,9 B 32,2 C 30,1 D 29,3 E 28,2
38

39. Séries Perpétuas
Os pagamentos
Valor Presente ou recebimentos
ocorrem até
o infinito.
0
Pagamentos ou recebimentos ad eternum.
39

40. Fórmulas para Séries Perpétuas
Sem crescimento :
• VP = PMT / i
Com crescimento :
• VP = PMT1 / (i-g)
Onde :
PMT1 = fluxo de caixa perpétuo no período 1
i = taxa de juros da operação ou custo de capital (deve ser maior que g)
g = taxa de crescimento do fluxo de caixa
40

41. Exercício de Fixação
Um título paga juros eternos anuais no
valor de $80. Se a taxa de juros
apropriada ao risco da operação é igual a
25% ao ano, qual o valor presente desse
papel?
A 240 B 280 C 320 D 360 E 400
41

42. Exercício de Fixação
 As ações da Rocambole S.A., prevêem pagar
um dividendo igual a $ 0,40 por ação no
próximo ano. Sabe-se que historicamente, os
dividendos da empresa crescem a uma taxa
igual a 2% a.a. e o custo de capital (i) da
empresa é estimado em 16% a.a. Qual o valor
da ação ?
A $ 2,5 B $ 2,17 C $ 2,86 D $3 E $ 3,86
42