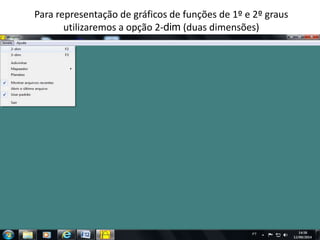
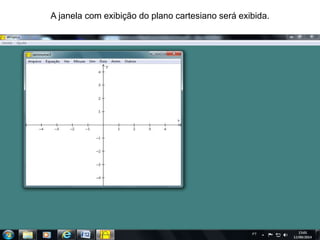
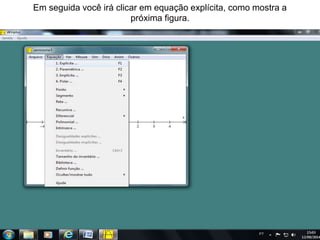
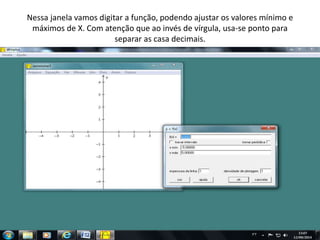
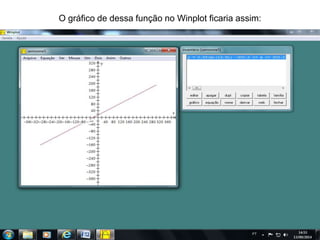
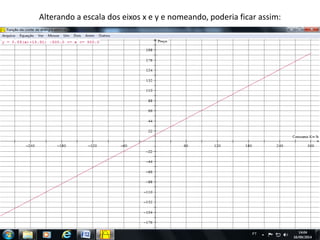
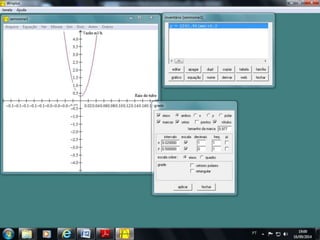
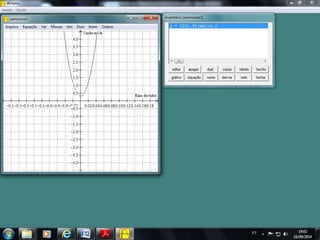
O documento discute como o software Winplot pode ser usado no ensino de funções polinomiais de 1o e 2o grau. Apresenta exemplos de como construir gráficos de funções lineares e parabólicas usando dados reais e discute como os gráficos podem ser usados para melhorar a compreensão dos alunos.

1. As Funcionalidades do Winplot no Ensino
de Funções Polinomiais
Elísio Henrique R da Silveira
09/2014

2. Objetivos do trabalho:
1. Mostrar ao aluno a presença das funções
polinomiais em seu cotidiano. Responder a
perguntas como: por que estudar
funções?
2. Construir um processo de ensino
aprendizagem atraente e interessante aos
olhos do aluno por meio dos recursos que
o software dispõe e também por meio de
aulas que explorem o dinamismo fugindo
do ensino puramente conteudista.
3. Aproveitar os recursos do software como
acelerador do processo de aprendizagem,
neste caso, para o ensino de funções

3. Para representação de gráficos de funções de 1º e
2º graus utilizaremos a opção 2-dim (duas
dimensões)

4. A janela com exibição do plano cartesiano será exibida.

5. Em seguida você irá clicar em equação explícita, como mostra a
próxima figura.

6. Nessa janela vamos digitar a função, podendo ajustar os
valores mínimo e máximos de X. Com atenção que ao invés
de vírgula, usa-se ponto para separar as casa decimais.

7. Exercícios sobre funções polinomiais envolvendo
situações do cotidiano.
Conta de energia elétrica.
Em uma conta de energia elétrica, o preço do kW/h é
dado pelo valor R$ 0,59062505. Acrescenta-se a conta a
pagar o valor de R$ 13,91 que é considerado nesta
situação uma constante. O consumo de energia elétrica
do mês de dezembro foi de 210,00 kw/h. Calcule pela
forma ax + b o valor total a ser pago e represente o
gráfico dessa função usando o Winplot.
Neste caso, o valor de a será 0,59062505, que é o preço
por Kw/h. O valor de x será o consumo que é a variável
da função. O valor de b será a constante 13,91.
Veja a ilustração:

9. O gráfico de dessa função no Winplot ficaria assim:

10. Alterando a escala dos eixos x e y e nomeando, poderia ficar assim:

11.  O Winplot oferece os recursos necessários para
tornar as atividades do ensino mais ágil, permitir
editar gráficos de rapidamente e de forma
precisa.
 Assim o professor poderia fazer perguntas
como:
 Se o consumo de energia do mês for de
240kw/h, qual seria o preço a pagar?
 Porque a reta do gráfico não toca no ponto
(0,0)?
 A função é crescente ou decrescente?

12. Caso envolvendo função polinomial do 2º grau.
O Esvaziamento do Tanque
Em uma estação de tratamento de
água, necessitam de reduzir o tempo
gasto para esvaziar um tanque de 14
m3/h. Para esvaziar o tanque são
usadas duas linhas de tubulação. Uma
das linhas tem vazão média de 0,3
m3/h . A outra tubulação tem diâmetro
de 2 polegadas (1” = 25,4mm). A
fórmula de vazão é: Q = A x V. A
velocidade média da água é de 2m/s =
720m/h

13.  Transformar 25,4mm em m:
0,0254m
 Q = vazão
 A = área da secção circular.
 V = velocidade da água.
 Q = 720
 Vamos chamar 720 de a, e r de x.
 Q = y

14. Dessa forma a equação do segundo
grau para volume da água ficará
assim:
Y = 1,46 + 0,3 = 1,76m3/h.
Agora vamos utilizar o Winplot para
estudar a alteração da vazão de
água em função do diâmetro da
tubulação .

17.  Com o gráfico pronto o professor poderá mostrar ao
aluno que sem necessidade de fazer cálculos será
possível verificar o volume (eixo y) para cada valor do
raio (eixo x), apenas correlacionando-os na curva da
parábola.
 Poderão ser levantadas questões como:
Porque o valor mínimo do y do vértice é 0,3?
Porque a curva do gráfico tem forma de parábola?