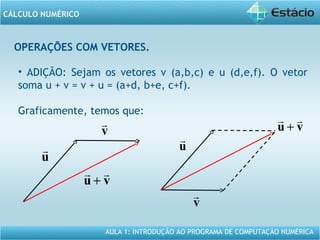
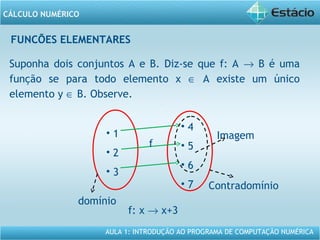
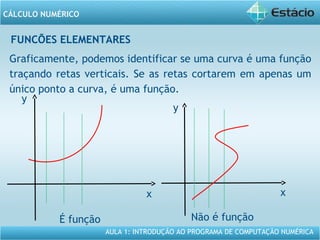
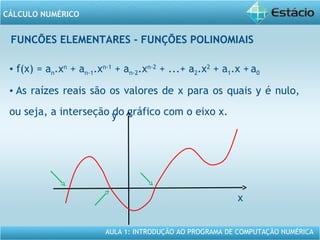
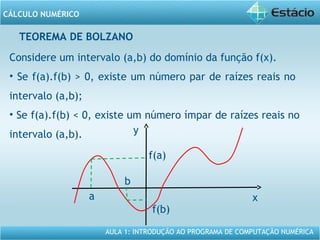
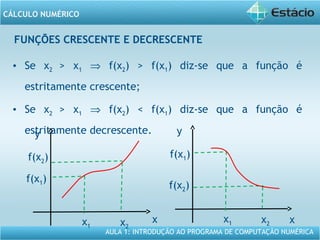
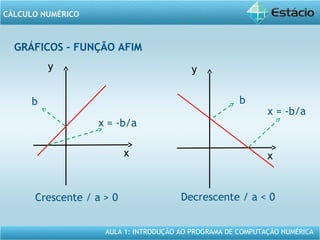
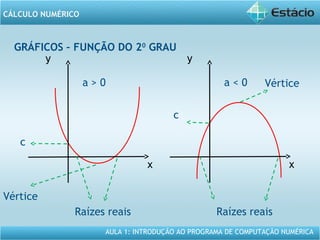
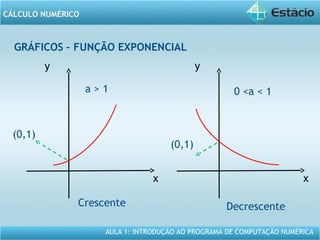
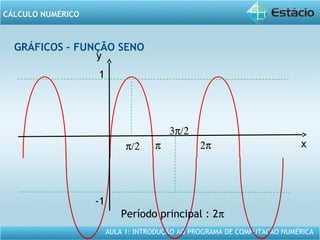
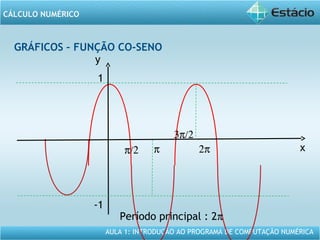
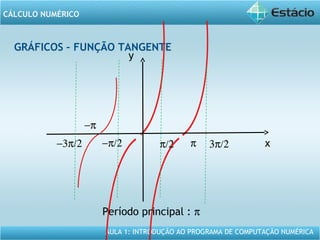
Este documento apresenta um resumo da Aula 1 do Programa de Computação Numérica sobre cálculo numérico. É introduzido o conteúdo programático da aula, que inclui operações com vetores, matrizes e funções. São também apresentados exemplos de aplicação dos conceitos, como multiplicação e adição de vetores, e propriedades de funções como crescente e decrescente.

1. CÁLCULO NUMÉRICO
Aula 1 – Introdução ao Programa de
Computação Numérica

2. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
CONTEÚDO PROGRAMÁTICO DESTA AULA
 Identificar e executar as operações
aritméticas:
 Escalares;
 Vetores;
 Matrizes;
 Identificar os tipos de funções e seus
respectivos gráficos;

3. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
VETORES – REPRESENTAÇÃO GRÁFICA
y
x
),( ba=v

a
b
y
x
),,( cba=v

a
b
c
z
jbia

.. +=v kcjbia

... ++=v

4. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM VETORES.
• MULTIPLICAÇÃO POR UM ESCALAR: Seja o vetor v (a,b,c) e
o escalar real α. O vetor α.v é dado por (α.a, α.b, α.c)
Ex.Se o vetor v é (1,2), o vetor 5.v será (5,10)
y
x
)2,1(=v

1
2
y
x
)10,5(=v

5
10

5. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM VETORES.
• ADIÇÃO: Sejam os vetores v (a,b,c) e u (d,e,f). O vetor
soma u + v = v + u = (a+d, b+e, c+f).
Graficamente, temos que:
v

u

vu

+
v

u

vu

+

6. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
Considere uma tabela com m linhas e n colunas em que
cada elemento que ocupa a “i-ésima” linha e a “j-ésima”
coluna é denominado aij










=
333231
232221
131211
aaa
aaa
aaa
A
Matriz com 3 linhas e 3 colunas. Matriz quadrada de ordem 3.

7. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
Multiplicação de uma matriz A por um escalar real α. Seja a
matriz Am x n. O produto de α por A, isto é, α.A é igual à
multiplicação de cada elemento aij por α.










=
333231
232221
131211
aaa
aaa
aaa
A










=
333231
232221
131211
...
...
...
.
aaa
aaa
aaa
A
ααα
ααα
ααα
α

8. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
Adição de matrizes – para que esteja definida entre duas
matrizes Am x n e Bp x q é necessário que m = p e n = q. Para
encontrar a matriz C = A + B, basta adicionar os elementos
respectivos, isto é, cij = aij + bij










+++
+++
+++
=










+










333332323131
232322222121
131312121111
333231
232221
131211
333231
232221
131211
bababa
bababa
bababa
bbb
bbb
bbb
aaa
aaa
aaa

9. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
Produto de matrizes – para que esteja definida entre duas
matrizes Am x n e Bp x q é necessário que o número de colunas
da primeira matriz seja igual ao número de linhas da segunda
matriz, isto é, n = p. A matriz produto terá o número de
linhas da primeira e o número de colunas da segunda, isto é,
m linhas e q colunas. Observe:
A3x4 . B4x5 = C3x5

10. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
Produto de matrizes – Uma vez que esta operação esteja
definida, cada elemento cij será formado pela multiplicação
dos elementos da linha i da matriz A pelos correspondentes
elementos da coluna j da matriz B.
Exemplo.
c32 = a31.b12 + a32.b22+a33.b32
244241
3231
2221
1211
233231
2221
1211
34434241
333231
232221
131211
.
x
x
x
cc
cc
cc
cc
bb
bb
bb
aaa
aaa
aaa
aaa














=

























11. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
OPERAÇÕES COM MATRIZES.
PROPRIEDADES:
• Em regra, Se A.B = B.A diz-se que A e B
comutam;
• A.I = A, I – matriz identidade
• A.(B+C) = A.B + A.C - distributiva à esquerda
• (B+C).A = B.A + C.A - distributiva à direita
• A.(B.C) = (A.B).C – associativa
• A.0 = 0, sendo 0, a matriz nula.
ABBA .. ≠

12. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
APLICANDO O CONHECIMENTO – EX 1
(PETROBRÁS - engenheiro) Sejam os vetores u = (1,2), v = (-2,5) e w = (x,y) do R2
. Para que w = 3u – v, devemos ter x + y igual a:
(PETROBRÁS - Engenheiro)
Sejam os vetores u = (1,2), v = (-2,5) e w = (x,y) do R2
. Para
que w = 3u – v, devemos ter x + y igual a?
SOLUÇÃO:
• Multiplicação de um escalar por um vetor:
 3u = 3.(1,2) = (3,6)
• Adição/subtração de vetores:
 3u – v = (3,6) – (-2,5) = (5,1) = w = (x,y)
• Por comparação, x = 5 e y = 1. Logo, x + y = 6

13. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
APLICANDO O CONHECIMENTO – EX 2
Considere as seguintes matrizes:
M = (mij)2x3, N = (nij)axb, P = (pij)cx4, Q = (qij)dxe.
Para que seja possível determinar M+N, NxP e P-Q, quais
os valores de a, b, c, d, e ?
SOLUÇÃO:
• ADIÇÃO: M2x3 + Naxb ⇒ a = 2 e b = 3
• MULTIPLICAÇÃO: M2x3.Pcx4 ⇒ c = 3
• SUBTRAÇÃO: Pcx4 – Qdxe ⇒ e = 4 e c =d = 3

14. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
FUNCÕES ELEMENTARES
Suponha dois conjuntos A e B. Diz-se que f: A → B é uma
função se para todo elemento x ∈ A existe um único
elemento y ∈ B. Observe.
f: x → x+3
domínio
• 1
• 2
• 3
• 4
• 5
• 6
• 7
f
Imagem
Contradomínio

15. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
FUNCÕES ELEMENTARES
Graficamente, podemos identificar se uma curva é uma função
traçando retas verticais. Se as retas cortarem em apenas um
único ponto a curva, é uma função.
x
y
É função
y
Não é função
x

16. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
FUNCÕES ELEMENTARES - FUNÇÕES POLINOMIAIS
• f(x) = an.xn
+ an-1.xn-1
+ an-2.xn-2
+ ...+ a2.x2
+ a1.x + a0
• As raízes reais são os valores de x para os quais y é nulo,
ou seja, a interseção do gráfico com o eixo x.
x
y

17. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
TEOREMA DE BOLZANO
Considere um intervalo (a,b) do domínio da função f(x).
• Se f(a).f(b) > 0, existe um número par de raízes reais no
intervalo (a,b);
• Se f(a).f(b) < 0, existe um número ímpar de raízes reais no
intervalo (a,b).
x
y
a
b
f(a)
f(b)

18. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
APLICANDO O CONHECIMENTO – EX 3
Seja a função polinomial f(x) = 2x3
- 12x2
-3x + 8. Mostre que
existe ao menos uma raiz real no intervalo (0, 1) da equação
f(x) = 0.
SOLUÇÃO:
 f(0) = 2.(0)3
– 12.(0)2
-3.(0) + 8 = 8
 f(1) = 2.(1)3
– 12.(1)2
-3.(1) + 8 = -5
Pelo Teorema de Bolzano, como f(0).f(1) < 0, podemos inferir
que existe um número ímpar de raízes reais no intervalo
(0,1).

19. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
FUNÇÕES CRESCENTE E DECRESCENTE
• Se x2 > x1 ⇒ f(x2) > f(x1) diz-se que a função é
estritamente crescente;
• Se x2 > x1 ⇒ f(x2) < f(x1) diz-se que a função é
estritamente decrescente.
x
y
x1 x2
f(x2)
f(x1)
x
y
x1 x2
f(x1)
f(x2)

20. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
FUNÇÕES ELEMENTARES.
• Função afim / linear: y = a.x + b
• Função quadrática: y = a.x2
+ b.x + c
• Função exponencial: y = ax
• Função Logarítmica: y = Logb(x)
• Função seno: y = sen(x)
• Função co-seno: y = cos(x)
• Função tangente: y = tg(x)

21. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO AFIM
y
x
y
x
Crescente / a > 0 Decrescente / a < 0
b b
x = -b/a
x = -b/a

22. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO DO 20
GRAU
y
x
a > 0
c
Raízes reais
Vértice
y
x
a < 0
c
Raízes reais
Vértice

23. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO EXPONENCIAL
y
x
a > 1
(0,1)
Crescente
y
x
0 <a < 1
Decrescente
(0,1)

24. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO SENO
y
x
1
-1
π/2 π
3π/2
2π
Período principal : 2π

25. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO CO-SENO
y
x
1
-1
π/2 π
3π/2
2π
Período principal : 2π

26. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
GRÁFICOS – FUNÇÃO TANGENTE
y
xπ/2 π 3π/2−π/2
Período principal : π
−π
−3π/2

27. AULA 1: INTRODUÇÃO AO PROGRAMA DE COMPUTAÇÃO NUMÉRICA
CÁLCULO NUMÉRICO
RESUMINDO
Nesta aula vocês estudaram:
 As operações aritméticas:
 Escalares;
 Vetores;
 Matrizes;
 Os tipos de funções e seus respectivos
gráficos.