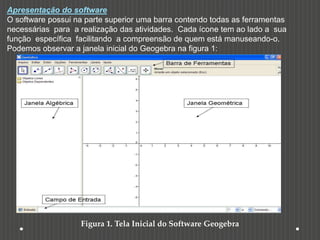
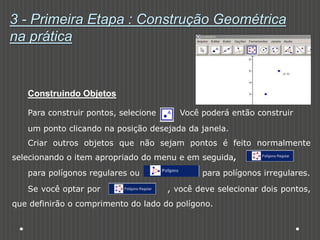
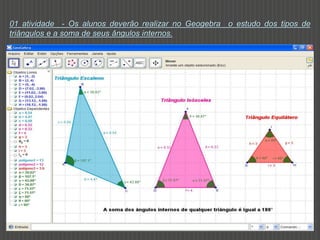
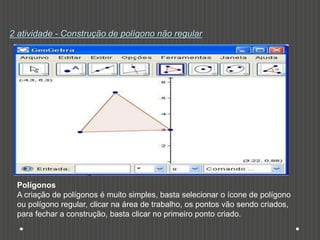
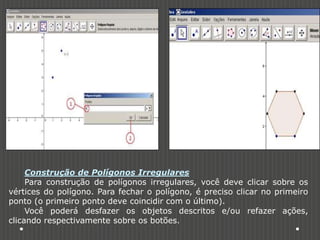
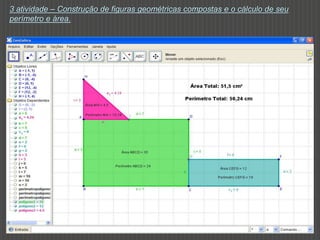
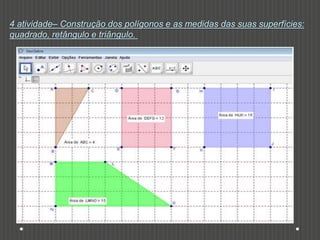
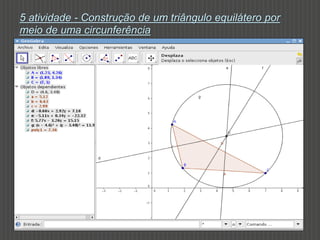
Este documento discute como o software Geogebra pode ser usado para ensinar construções geométricas de forma dinâmica e interativa. Ele descreve cinco atividades com Geogebra para estudar tipos de triângulos, polígonos regulares e irregulares, figuras geométricas compostas e suas medidas de perímetro e área. O documento conclui que o uso de tecnologia como o Geogebra pode tornar o ensino de geometria mais atraente e envolver os alunos na construção de seu próprio conhecimento.

1. CONSTRUÇÕES GEOMÉTRICAS
COM GEOGEBRA
Andrea Takaki
Polo.: São Paulo CEU Jardim Paulistano
(JPA) – SP – 2015 Grupo.: 06

2. Primeira Etapa : Introdução a Geometria
Neste primeiro momento daremos uma breve introdução no
reconhecimento das funções e da História da Construção da
Geometria em sala de aula. Material didático para turmas do 5o ao 6o
ano do Ensino Fundamental, o professor deverá trabalhar em 2 aulas
de 50 minutos falar sobre as construções geométricas por régua e
compasso antes de inseri-las nas resoluções de questões.
O professor formará pequenos grupos de alunos , para a análise de
uma diversidade de livros didáticos de matemática, com foco nos
conteúdos relacionadas à geometria trabalhada de 5ª a 6ª série da
Educação Básica. Abrir uma discussão em relação às diferentes
formas em que os autores abordam conceitos, propriedades e
representações geométricas.
Os alunos poderão trabalhar em grupos ou individualmente nas
resoluções das atividades em sala de aula.

3. Conhecendo um pouco do software Geogebra
O Geogebra é um software de matemática dinâmico, criado pelo professor Dr.
Markus Hohenwarter da Flórida Atlantic University, em 2001, que reúne
recursos de geometria, álgebra e cálculo. É um software gratuito, escrito na
linguagem JAVA e disponível em rede para download no seguinte endereço:
http://www.geogebra.org/cms/pt_BR. É compatível com diferentes sistemas
operacionais, entre eles, o Microsoft Windows 98, 2000, XP, Vista, Seven (32
e 64 bits) e Linux. O trabalho no software é simples e fácil, e por isso pode
ser usado tanto na educação básica como no ensino superior.
Segundo Hohenwarter (2007), criador do software, a característica mais
destacável do Geogebra é a percepção dupla dos objetos: cada expressão na
janela algébrica corresponde a um objeto na janela gráfica e vice-versa.
Dessa forma o aluno tem a possibilidade de visualizar aquilo que está
calculando, facilitando a compreensão do conteúdo trabalhado.
Esse aplicativo permite a realização de diferentes atividades, entre elas,
podemos destacar a construção de pontos, segmentos de reta, retas
paralelas e perpendiculares, construção de gráficos de funções, construção
de figuras geométricas, permite ainda calcular o ponto médio dos segmentos,
a área, o perímetro das figuras, medir ângulos, entre outras.

4. Segunda Etapa: Construções Geométricas
Despertar no aluno o interesse pela geometria é um dos objetivos da
maioria dos professores. A necessidade de melhorar a aprendizagem e de
romper com métodos de ensino arcaicos e de pouca inclusão, nos leva a
busca de uma ferramenta moderna, socializadora e que atraia a atenção
dos estudantes.
O programa Geogebra possibilita que as construções geométricas, sejam
feitas de maneira dinâmica e interativa, permitindo que as técnicas de
construções geométricas, sejam exploradas com mais riqueza de
detalhes que as construções tradicionais. A partir dessa análise, optou-se
por utilizar nesse trabalho, o software Geogebra.

5. Apresentação do software
O software possui na parte superior uma barra contendo todas as ferramentas
necessárias para a realização das atividades. Cada ícone tem ao lado a sua
função específica facilitando a compreensão de quem está manuseando-o.
Podemos observar a janela inicial do Geogebra na figura 1:
Figura 1. Tela Inicial do Software Geogebra

6. Construindo Objetos
Para construir pontos, selecione . Você poderá então construir
um ponto clicando na posição desejada da janela.
Criar outros objetos que não sejam pontos é feito normalmente
selecionando o item apropriado do menu e em seguida,
para polígonos regulares ou para polígonos irregulares.
Se você optar por , você deve selecionar dois pontos,
que definirão o comprimento do lado do polígono.
3 - Primeira Etapa : Construção Geométrica
na prática

7. 01 atividade - Os alunos deverão realizar no Geogebra o estudo dos tipos de
triângulos e a soma de seus ângulos internos.

8. 2 atividade - Construção de polígono não regular
Polígonos
A criação de polígonos é muito simples, basta selecionar o ícone de polígono
ou polígono regular, clicar na área de trabalho, os pontos vão sendo criados,
para fechar a construção, basta clicar no primeiro ponto criado.

9. .
Construção de Polígonos Irregulares
Para construção de polígonos irregulares, você deve clicar sobre os
vértices do polígono. Para fechar o polígono, é preciso clicar no primeiro
ponto (o primeiro ponto deve coincidir com o último).
Você poderá desfazer os objetos descritos e/ou refazer ações,
clicando respectivamente sobre os botões.

10. 3 atividade – Construção de figuras geométricas compostas e o cálculo de seu
perímetro e área.

11. 4 atividade– Construção dos polígonos e as medidas das suas superfícies:
quadrado, retângulo e triângulo.

12. 5 atividade - Construção de um triângulo equilátero por
meio de uma circunferência

13. Considerações finais
As atividades desenvolvidas com o software Geogebra mostraram-nos que é
possível ensinar Geometria de forma dinâmica, tornando a aula instigante e
atrativa, na qual o aluno participa, interage com seus colegas, e através de suas
construções vai formulando o seu próprio conhecimento. Tudo isso vem a
contribuir para o aumento das habilidades e potencialidades dos educandos, que
nada mais é, do que nosso objetivo como futuros docentes.
Esta experiência mostrou-nos também, a importância da inserção dos recursos
tecnológicos no âmbito escolar de forma geral, pois muitas são as contribuições
que os mesmos podem proporcionar à aprendizagem. Através de seu uso é
possível ampliar as oportunidades de aprendizagem do usuário, além de
contribuir na estruturação de um raciocínio diferenciado em termos de eficiência,
rapidez e precisão.

14. • Bibliografia :
Sites da internet
www .geogebra.org
EVES, H. Introdução a História da Matemática. Tradução de Higino H.
Domingues. Campinas, São Paulo: Unicamp, 1994. 844 p.
GUERRA, V.C. Impossibilidades em Construções Geométricas: Aspectos
Históricos e Matemáticos. Disponível em: . Acesso em 20 de Dezembro de
2012
WAGNER, E. Construções Geométricas. Com a colaboração de João
Paulo Carneiro. Coleção do Professor de Matemática. SBM, 1993, 110 p.
http://www.sbembrasil.org.br/sbembrasil/images/arquivos/Mini-curso.pdf