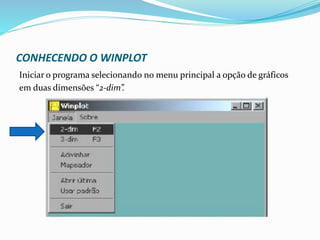
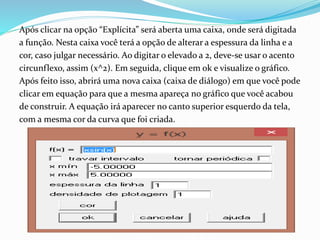
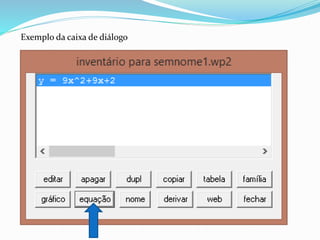
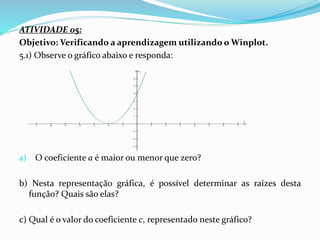
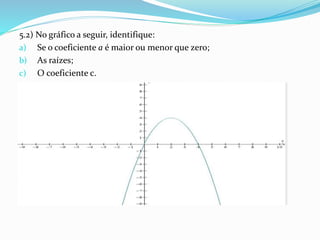
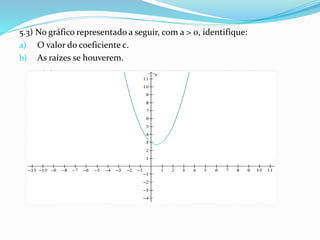
O documento apresenta uma proposta de atividade sobre equações do 2° grau para alunos do 9° ano do ensino fundamental utilizando o software Winplot. A atividade inclui instruções sobre como utilizar o Winplot para desenhar gráficos de funções do 2° grau, análises desses gráficos e exercícios para verificar a compreensão dos alunos.

1. NOVAS TECNOLOGIAS NO ENSINO
DE MATEMÁTICA

2. Informática Educativa
 Edna Mateus Pinto
 Grupo 01

4. CARACTERÍSTICAS TÉCNICAS DO WINPLOT
O Winplot é um programa que foi desenvolvido por volta de 1985, pelo
Professor Richard Parris “Rick”, da Philips Exeter Academy, em linguagem
C. Chamava-se Plot e rodava no DOS, com o surgimento do Windows 3.1
passou a se chamar Winplot. A versão para ser utilizada no Windows 98
surgiu em 2001 e foi escrita na linguagem C++.
O software foi traduzido para o português pelo professor Adelmo Ribeiro
de Jesus e nas versões recentes tem a participação do professor Carlos
César de Araújo. (FERREIRA; CAMPOS; DIAS).
É um software gratuito, pequeno, com capacidade de 812 Kb, versão em
português e pode ser instalado em sistemas Windows XP/98/2000 e Linux.

5. OBJETIVOS
Objetivo geral:
Elaborar uma proposta de atividade sobre Equação do 2° grau, com o
uso do software educacional Winplot, para ser aplicada às turmas de 9°
ano do Ensino Fundamental.
Objetivos específicos:
Desenhar gráficos de funções do 2° grau com a utilização do software
educacional.
Compreender o comportamento das funções, quando a concavidade
está voltada para cima ou para baixo.
Visualizar os diferentes tipos de gráficos em relação aos coeficientes a e
c e aos deltas (Δ) maiores, menores ou iguais a zero.
Verificar se o uso de novas tecnologias facilita o processo de ensino e
aprendizagem.

6. METODOLOGIA
Pretende-se introduzir o conteúdo de Equação do 2° grau, em turmas de
9° ano do Ensino Fundamental, com o objetivo de permitir aos
estudantes a construção do conhecimento de maneira diferenciada e
inovar a prática pedagógica do educador.
No intuito de contribuir com o processo de aprendizagem, será utilizado
material concreto, neste caso em específico, cartões feitos de cartolina
em formatos quadrados e retangulares, para calcular raízes de uma
Equação do 2° grau, pelo método de Al-Khowarizmi.
Quando for iniciado o estudo dos gráficos, os estudantes serão
direcionados ao laboratório de informática para conhecerem o Winplot,
que é um software livre, considerado como um recurso facilitador na
visualização de gráficos e variação no comportamento das funções.

7. Por ser um software de instalação gratuita não haverá custo para o projeto
e os estudantes serão orientados a instalarem o mesmo em casa, para que
possam desenvolver e aprimorar o que foi assimilado em sala de aula.
Na aula laboratorial, será fornecido um roteiro de trabalho aos estudantes
onde deverão, com o auxílio do software, esboçar os gráficos das funções do
2° grau, fazendo análise e registros nos cadernos, sobre o comportamento das
mesmas.
Os estudantes serão divididos em duplas para a realização desta atividade e o
professor irá instruí-los passo-a-passo a realizar alguns procedimentos.
Pretende-se com essas didáticas, inserir o conteúdo de Equações do 2° grau,
permitindo que os estudantes interajam com a aula de forma dinâmica e
construam o conhecimento de forma significativa.

8. CONHECENDO O WINPLOT
Iniciar o programa selecionando no menu principal a opção de gráficos
em duas dimensões “2-dim”.

9. Selecionar no menu principal a opção “Equação” e em seguida, clicar em
“Explícita”.

10. Após clicar na opção “Explícita” será aberta uma caixa, onde será digitada
a função. Nesta caixa você terá a opção de alterar a espessura da linha e a
cor, caso julgar necessário. Ao digitar o elevado a 2, deve-se usar o acento
circunflexo, assim (x^2). Em seguida, clique em ok e visualize o gráfico.
Após feito isso, abrirá uma nova caixa (caixa de diálogo) em que você pode
clicar em equação para que a mesma apareça no gráfico que você acabou
de construir. A equação irá aparecer no canto superior esquerdo da tela,
com a mesma cor da curva que foi criada.

11. Exemplo da caixa de diálogo

12. ROTEIRO DE ATIVIDADES
ATIVIDADE 01:
Objetivo: Esboçar gráficos de funções do 2° grau.
Seguindo os passos anteriores “Conhecendo o Winplot”, esboce o gráfico da
função f(x) = x² + 6x + 9.
Caso não consiga visualizar bem o gráfico, você pode usar as teclas PgUp
(aproximar) ou PgDn (afastar), até que fique bem visível.
Feito isso, “Parabéns”, você acabou de esboçar o gráfico de uma função do 2°
grau.
Agora salve-o. Vá no menu “Arquivo” e em seguida, “Salvar como” e grave-o
com o nome de gráfico 1.

13. ATIVIDADE 02:
Objetivo: Esboçar gráficos de funções com a > 0 e a < 0.
Esboce o gráfico das seguintes funções:
a) f(x) = x² - 2x – 3
b) f(x) = 2x² + 1
c) f(x) = -x² + 4x
d) f(x) = -2x² - 4x + 1
e) f(x) = 2x²
f) f(x) = -x²
OBS.: Você deve ter observado que o gráfico de uma função do 2° grau é uma
curva. Essa curva é chamada parábola. Sua concavidade pode ser voltada
para cima ou para baixo.

14. Sobre os gráficos construídos anteriormente, responda:
2.1) Que relação existe entre o coeficiente a e a posição da parábola
(concavidade voltada para cima ou para baixo)?
2.2) A parábola corta o eixo x em quantos pontos?
2.3) A parábola corta o eixo y em quantos pontos?
2.4) Como podemos descobrir os pontos (se existirem) em que a
parábola intersecta o eixo x?
2.5) Em qual ponto a parábola intersecta o eixo y?
2.6) Em que casos a parábola passa pela origem, ou seja, ponto (0,0)?

15. ATIVIDADE 03:
Objetivo: Observar o comportamento das funções quando a > 0, a < 0
e o ponto que intersecta o eixo y.
Para que possam melhor compreender o conteúdo de Equação do 2° grau,
após instalarem o software em casa, os estudantes deverão com o auxílio
do mesmo esboçar o gráfico das funções f(x) = x² - 6x + 5; f(x) = -x²+ 7x – 10
e para cada uma delas, responder:
a) Este gráfico tem concavidade voltada para cima ou para baixo?
b) Ele intersecta o eixo x? Em que ponto?
c) Ele intersecta o eixo y? Em que ponto?
d) O ponto (3,-4) pertence ao gráfico?
e) O ponto (2,0) pertence ao gráfico?

16. ATIVIDADE 04:
Objetivo: Esboçar gráficos de funções de 2° grau, com >, < ou = 0.
Utilizando o software Winplot, esboce o gráfico das funções:
a) f(x) = 9x² - 4x
b) f(x) = -x²+ 7x - 10
c) f(x) = x² - 6x + 9
d) f(x) = x² +12x + 36
e) f(x) = 5x² - 3x + 1
f) f(x) = x² - 2x + 5
Para cada um dos gráficos esboçados, responda:
4.1) Em quantos pontos o gráfico intersecta o eixo x? Quais são eles?
4.2) O que os pontos que intersectam o eixo x representam no gráfico?

17. ATIVIDADE 05:
Objetivo: Verificando a aprendizagem utilizando o Winplot.
5.1) Observe o gráfico abaixo e responda:
a) O coeficiente a é maior ou menor que zero?
b) Nesta representação gráfica, é possível determinar as raízes desta
função? Quais são elas?
c) Qual é o valor do coeficiente c, representado neste gráfico?
             













x
y

18. 5.2) No gráfico a seguir, identifique:
a) Se o coeficiente a é maior ou menor que zero;
b) As raízes;
c) O coeficiente c.

19. 5.3) No gráfico representado a seguir, com a > 0, identifique:
a) O valor do coeficiente c.
b) As raízes se houverem.

20. CONCLUSÃO
Este projeto fundamentou-se em elaborar atividades relacionadas ao
conteúdo de Equações do 2° grau, utilizando o software educacional
Winplot, como recurso facilitador para visualização dos gráficos.
À medida que os professores tem a possibilidade de inovar sua didática
utilizando um recurso diferenciado, eles estão auxiliando os estudantes
no processo de abstração, generalização e permitindo a estes o
desenvolvimento e aprimoramento do pensamento matemático.
No intuito de possibilitar a compreensão dos estudantes, o professor deve
buscar aprimorar suas estratégias de ensino e estar disposto a permitir que
estes se apropriem dos conhecimentos de forma relevante.

21. Considero que o ensino de conteúdos relacionados ao uso de tecnologias,
além de proporcionar maior interação entre professores e estudantes,
possibilita a estes últimos a construção e a resignificação do pensamento
matemático.
Acredita-se, portanto, que essa abordagem, possa ser desenvolvida dentro
de um contexto motivador, a partir da problematização do saber, além de
orientar a prática educativa e promover a reflexão do educador sobre as
finalidades do ensino de Matemática, em particular, do ensino de
Equações do 2° grau.

22. REFERÊNCIAS
DANTE, L.R. Tudo é Matemática. 2. ed. Rio Claro: São Paulo, Ed. Ática,
2008.
FERREIRA, S. E.; CAMPOS, F. O.; DIAS, A. O. Softwares em ambientes
educacionais. Disponível em: <
http://www.pucrs.br/famat/viali/tic_literatura/artigos/pacotes/Softwarese
mambienteseducacionais.pdf>. Acesso em: 03 Mar. 2016.
VIVENDO entre símbolos. Disponível em:
http://www.vivendoentresimbolos.com/2013/02/o-metodo-de-completar
quadrados_20.html>. Acesso em: 21 Mar. 2016.
WINPLOT. Disponível em:
<http://www.baixaki.com.br/download/winplot.htm>. Acesso em: 20 Mar.
2016.