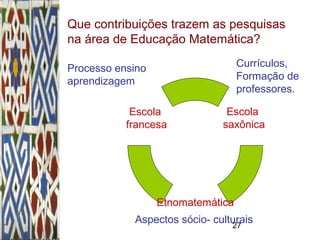
O documento discute os desafios da Educação Matemática como área de conhecimento em construção. Apresenta a trajetória da Educação Matemática no Brasil desde as décadas de 1930 e 1940, destacando figuras como Euclides Roxo e Júlio César de Mello e Souza. Também aborda as principais tendências que orientam a Educação Matemática mundialmente e os desafios de colocar em prática os avanços das pesquisas na área.