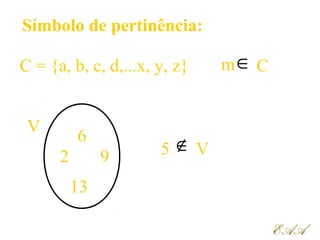
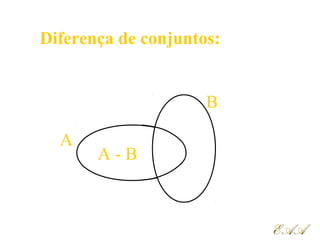
1) A aula introdutória sobre conjuntos tem como objetivo apresentar os conceitos básicos de forma clara para os alunos do 1o ano do ensino médio. 2) Conjuntos são coleções de elementos que podem ser representados por letras maiúsculas e símbolos matemáticos. 3) As operações com conjuntos incluem união, interseção, diferença e complemento.

1. Aula de álgebra destinada a alunos do 1o
ano do ensino médio do CEAL.
EAAEAA
Professora Enoêmia

2. EAAEAA
Este trabalho é o resultado de um
apanhado geral sobre introdução
elementar à teoria dos conjuntos, em
diversas fontes bibliográficas.

3. O objetivo desta aula, é introduzir os
conceitos fundamentais de conjuntos de
forma clara e objetiva, para que se tenha
uma melhor compreensão e interesse por
parte dos alunos e assim, adquirir base
para o desenvolvimento de temas futuros,
a exemplo de relações, funções, análise
combinatória, probabilidades, etc.
EAAEAA

4. Conjuntos
Conjunto: representa uma coleção ou
reunião de elementos, independente
da ordem em que se apresentam.
EAAEAA

5. EAAEAA
Conjunto de flores
Conjunto de cãesConjunto de colheres
Conjunto de frutas

6. Em geral, um conjunto é denotado por
uma letra maiúscula do Alfabeto:
A, B, C, ..., Z.
EAAEAA
N = {0, 1, 2, 3, 4, 5, 6,...}
Q = {0, , 1, , 2, 3, 4,...}
2
1
2
3

7. Elemento:
É um dos componentes de um conjunto.
X
EAAEAA
{= 1 2 3 4 5, }, , ,

elementos

8. Representação de conjuntos:
{ }
A= { }
P 0
3
2
5
x/x é letra do alfabeto
EAAEAA
Chaves
Descrito por propriedades
Diagrama de Venn-Euler

9. Símbolo de pertinência:
C = {a, b, c, d,...x, y, z} m C∈
6
13
92 5 V
V
∉
EAAEAA

10. Conjuntos especiais
-Conjunto vazio: ou {}
EAAEAA

11. Conjunto universo U
= {a, b, c}.I = {a, b},
W = {b, c}
J = {a},
F = {a, c},
T = {c},O = {b},P = {},
H
Então, H é o conjunto universo.
EAAEAA
Dados os conjuntos:
Se U é o conjunto que contém todos os
conjuntos relacionados.

12. Subconjuntos
Dados os conjuntos
B = {5, , , , 15, 16, }.
A = { , , , } e
8 9 10 18
8 9 10 18
EAAEAA
Se os elementos 8,9,10 e 18 A e B,
temos que; A é subconjunto de b.
∈
B
AGraficamente temos,

13. ⊂
⊄
⊃
⊃
Relação de subconjuntos.
está contido
contém
Não está contido
não contém
EAAEAA

14. Dados os conjuntos I={3, 7, 8, m, p, c, d},
J
J = {8, p, d},
H = {f, 7, 8}.
P = {3, 7, m, c} e
I
I P
I H⊃
⊃ ⊂
⊂
⊃ ⊂
J I
IP
IH
ou
ou
ou
EAAEAA

15. OPERAÇÕES COM CONJUNTOS
EAAEAA

16. Reunião de conjuntos ∪
Dados A =
B =
{∪
EAAEAA
A = a, v, m, 3, 9,11

B

A
}
ea, v, m}{
{3, 9, 11}
+
B

17. Interseção de Conjuntos∩
Dados G = { 2, , } e
D = {3, , ,11}
G ∩
5
5 9
95,
9
EAAEAA
= }{B
Os elementos 5 e 9 G e também D,∈ ∈
logo, a interseção de G e D é:

18. Diferença de conjuntos:
A
B
EAAEAA
A - B

19. Complemento C
B
AC
EAAEAA
= A - B

20. Número de elementos da reunião de dois
conjuntos A e B.
n(A B) = n(A) + n(B) – (A B)∩
EAAEAA
∪

21. Sendo A = {0, 3, 5, 7, 9}
B = {1, 3, 4, 5, 7, 8, 9}.
n(A B) = ∩
Determine n(A B).∪
n(A B) = 5 + 7 - 4
8
n(A) + n(B) - (A B)
EAAEAA
∪
∪
n(A B) =∪

22. GIOVANNI, José Ruy e Giovanni Jr.
Matemática fundamental: uma nova abor-
dagem: ensino médio: volume único.
São Paulo, FTD 2002.
Dante, Luiz Roberto. Matemática, volume
único: 1a edição, São Paulo: Àtica, 2005.
Fontes bibliográficas.

23. GENTIL, Nelson. Matemática para o 2o
grau, volume 1, 5a
edição, São Paulo: Ática
1996.
http:/www.brasilescola.com/matemtica/
funções.htm