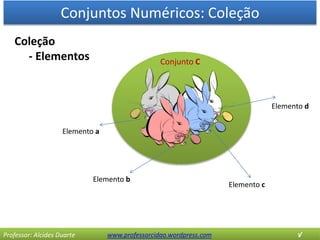
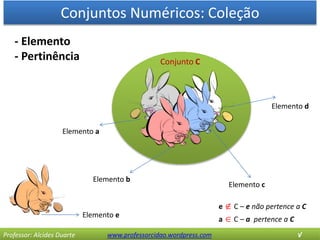
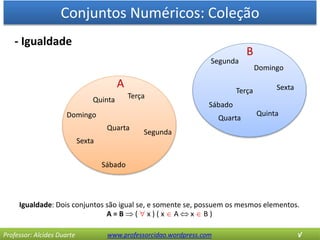
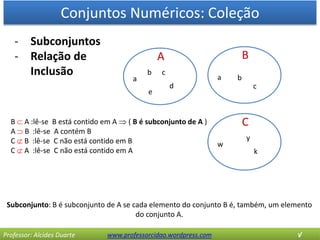
O documento discute os conceitos básicos de conjuntos numéricos, incluindo: 1) coleções de elementos e suas propriedades como pertinência e igualdade; 2) tipos de conjuntos como vazio, unitário e universo; 3) operações entre conjuntos como união, interseção e diferença; e 4) o conjunto de partes formado por todos os subconjuntos de um dado conjunto.












![Conjuntos Numéricos: Partes
Professor: Alcides Duarte www.professorcidao.wordpress.com √
Conjunto das Partes: O conjunto das partes de A que se indica por P(A) é o conjunto cujos
elementos são subconjuntos de A: P(A) = {x A/ x A}
A = { 10, 20 }
Os subconjuntos de A, são: {10} ; {20} ; {10, 20} ; .
P(A) = { {10} ; {20} ; {10, 20} ; }
número de elementos de um
conjunto das partes é dado
por 2n
n [ P(A) ] = 22 = 4](https://image.slidesharecdn.com/conjuntosnumricos-140527082245-phpapp02/85/Conjuntos-Numericos-18-320.jpg)
![Conjuntos Numéricos: Partes
Professor: Alcides Duarte www.professorcidao.wordpress.com √
• se A = {2}, então P(A) = { {2}, { } }
• se A = , P(A) = { }, que não é vazio.
• se A = {5, 10, 15, 20}, então
P(A) = { {5}, {10}, {15}, {20},
{5,10}, {5,15}, {5,20}, {10,15}, {10,20}, {15,20},
{5,10,15}, {5,10,20}, {5,15,20}, {10,15,20},
{5, 10, 15, 20}, { } }
número de elementos de um
conjunto das partes é dado
por 2n
n [ P(A) ] = 21 = 2
n [ P(A) ] = 24 = 16
n [ P(A) ] = 21 = 2](https://image.slidesharecdn.com/conjuntosnumricos-140527082245-phpapp02/85/Conjuntos-Numericos-19-320.jpg)
