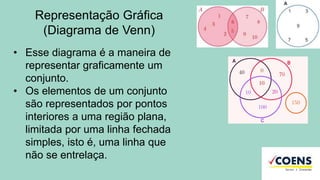
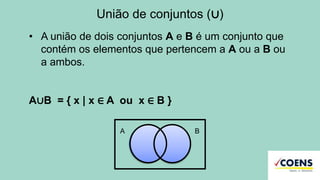
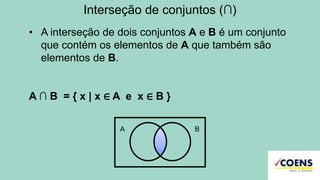
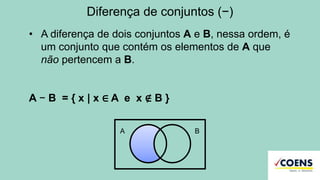
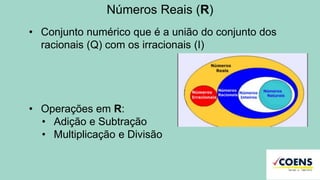
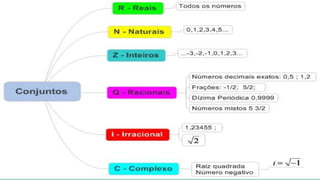
A teoria dos conjuntos é uma base matemática para agrupar elementos, podendo ser representada de várias formas, como tabular, por propriedade característica e graficamente. Os tipos de conjuntos incluem unitário, vazio, finito, infinito, entre outros, e operações com conjuntos abrangem união, interseção e diferença. O documento também aborda subconjuntos e conjuntos numéricos como naturais, inteiros, racionais e irracionais.

1. Teoria dos Conjuntos
www.coens.com.br

2. Conceito Primitivo
A teoria dos conjuntos é a teoria matemática capaz
de agrupar elementos.
Exemplo: Um time de basquete é um conjunto; onde
cada jogador do time é um elemento desse conjunto.

3. Representação de um Conjunto
• Representação Tabular;
• Através de Propriedade Caraterística;
• Representação Gráfica (Diagrama de Venn).

4. Representação Tabular
• Podemos representar um conjunto na forma de
tabela, escrevendo seus elementos entre chaves { }
e separados por vírgula.
• É usual representarmos os conjuntos por letras
maiúsculas A, B, C, D, ...
• A = {a, e, i, o, u}
• B = {1, 2, 3, 4}

5. Propriedade Característica
• Nesse modelo de representação, um conjunto pode
ser enunciado por uma propriedade ou condição
relacionada aos seus elementos
• :
A = { x | x tem a propriedade p }.
"A é o conjunto formado por todos os elementos x tal
que x tem a propriedade p".

6. Propriedade Característica
Exemplos:
• A = {x | x é país da Ásia} - o conjunto A é formado
por todos os países da Europa.
• B = {x | x é cor da bandeira de Patos de Minas} - o
conjunto B é formado por verde, amarelo, azul e
branco.

7. Representação Gráfica
(Diagrama de Venn)
• Esse diagrama é a maneira de
representar graficamente um
conjunto.
• Os elementos de um conjunto
são representados por pontos
interiores a uma região plana,
limitada por uma linha fechada
simples, isto é, uma linha que
não se entrelaça.

8. Exercícios Teoria dos Conjuntos
(PUC- PR) Em um levantamento com 100 vestibulandos da PUC, verificou-se que o
número de alunos que estudou para as provas de Matemática, Física e Português foi o
seguinte: Matemática, 47; Física, 32; Português, 21; Matemática e Física, 7; Matemática e
Português, 5; Física e Português, 6; as três matérias, 2. Quantos dos 100 alunos incluídos
no levantamento não estudaram nenhuma das três matérias?

9. Relação de pertinência
Dado o conjunto A = {a, e, i, o, u}.
• Note que a letra ”u” é elemento do conjunto A;
• A letra ”f” não é elemento do conjunto A.
• ”u” ∈ A (lê-se ”u pertence a A”)
• ”f” ∉ B (lê-se ”f não pertence a A")
 a
 e
 i
 o
 u
A

10. Exercício Teoria dos Conjuntos
(MACKENZIE-SP) Se A e B são dois conjuntos tais que A ⊂ B e A ≠ ∅, então:
(A) sempre existe x ∈ A tal que x ∉ B.
(B) sempre existe x ∈ B tal que x ∉ A.
(C) se x ∈ B então x ∈ A.
(D) se x ∉ B então x ∉ A.
(E) A ∩ B = ∅.

11. Tipos de Conjuntos
1) Conjunto unitário
2) Conjunto vazio
3) Conjunto finito
4) Conjunto infinito
5) Conjuntos iguais
6) Conjunto universo
7) Conjuntos disjuntos

12. Conjunto Unitário
• Conjunto unitário é aquele formado por um único
elemento.
Exemplos:
• A = { 2 }
• C = { x | x ∈ N | x < 4 } = { 3 }

13. Conjunto Vazio
• Conjunto vazio é o conjunto que não possui nenhum
elemento.
• Conjunto vazio é representado por Ø ou { }.
Exemplo:
• D = {x | x é um número ímpar múltiplo de 6} = Ø

14. Conjunto Finito
• Conjunto finito representa uma quantidade limitada
de elementos ou é aquele que conseguimos chegar
ao "fim" da contagem de seus elementos.
Exemplos:
• B = {1, 2, 3, 4}
• H = {x | x é uma cidade do estado da Bahia}

15. Conjunto Infinito
• Conjunto infinito Apresenta uma quantidade infinita
(ilimitada de termos) ou é aquele que, se contarmos
seus elementos um a um, jamais chegaremos ao
"fim" da contagem.
Exemplos:
• N = { 0, 1, 2, 3, 4, ... }
• A = { x ∈ N | x é par } = { 2, 4, 6, ... }

16. Conjuntos Iguais
• Conjuntos são iguais quando possuem os mesmos
elementos, podem ser dois ou mais conjuntos.
Exemplo:
• A = {m, a, r, e} e B = {r, e, m, a}, temos A = B
• Pois os conjuntos possuem os mesmos elementos,
não importando a ordem em que os elementos
foram escritos.

17. Conjunto Universo
• É um conjunto ao qual pertencem todos os
elementos de um estudo
• Exemplo: Quais são os números menores que 5?
• Se o conjunto universo for = {0, 1, 2, 3, 4}
• Se o conjunto universo for = {..., -1, 0, 1, 2, 3, 4}

18. Tipos de Conjuntos
Conjuntos Disjuntos
• São conjuntos que não possuem nenhum elemento
em comum.
Exemplo:
• Sendo os conjuntos A = {x | x é par} e B = {x | x é
ímpar} ➪ A e B são conjuntos disjuntos.

19. • Sendo A e B, diz-se que A é subconjunto de B se,
e somente se, todo elemento de A pertence a B.
• A ⊂ B (lê-se "A está contido em B")
• B ⊃ A (lê-se "B contém A”)
Exemplos:
• {2, 5, 3} ⊂ {2, 5, 3, 8, 9}
• {6, 9, 8, 5} ⊃ {9, 6}

20. Conjunto das Partes
• Sendo A = {c, d}. Vamos determinar os
subconjuntos de A:
P(A) = { Ø, {p}, {h}, {p, h} }
• Chamamos conjunto das partes de um conjunto H
ao conjunto cujos elementos são todos os
subconjuntos de H.
• Notação: P(H) (lê-se P de H)

21. Número de elementos de P(A)
• De um modo geral, se um conjunto A tem n
elementos, os números de elementos
(subconjuntos) de P(A) = 2n.
Exemplos:
• A = {a, b} ➪ P(A) = 22 = 4 subconjuntos.
• B = {a, b, c} ➪ P(B) = 23 = 8 subconjuntos.

22. Operações com Conjuntos
Operações com Conjuntos
• União
• Interseção
• Diferença
• Complementar

23. União de conjuntos (∪)
• A união de dois conjuntos A e B é um conjunto que
contém os elementos que pertencem a A ou a B ou
a ambos.
A∪B = { x | x ∈ A ou x ∈ B }
A B

24. Exemplos de União (∪)
• Dados os conjuntos A={ 2,3,5,6,8 } e B={ 3,5,8,9 }
A U B = { 2, 3, 5, 6, 8, 9 }
• Dados os conjuntos A={ 3,5 } e B={ 2,3,4,5,6 }
A U B = { 2, 3, 4, 5, 6 } = B
U = União

25. Interseção de conjuntos (∩)
• A interseção de dois conjuntos A e B é um conjunto
que contém os elementos de A que também são
elementos de B.
A ∩ B = { x | x ∈ A e x ∈ B }
A B

26. Exemplos de Interseção (∩)
• Dados os conjuntos A={2,3,5,6,8} e B={3,5,8,9}
A ∩ B = {3, 5, 8}
• Dados os conjuntos A={3,5} e B={2,3,4,5,6}
A ∩ B = {3,5} = A
∩ = Interseção

27. Diferença de conjuntos (−)
• A diferença de dois conjuntos A e B, nessa ordem, é
um conjunto que contém os elementos de A que
não pertencem a B.
A − B = { x | x ∈ A e x ∉ B }
A B

28. Exemplo de Diferença (−)
• Dados os conjuntos A={2,3,5,6,8} e B={3,5,8,9}
A − B = {2, 6}
B − A = {9}
• Dados os conjuntos A={3,5} e B={2,3,4,5,6}
A − B = { } = Ø
B − A = {2, 4, 6}

29. Complementar de um conjunto
• O conjunto complementar de A (denotado por CA) é
o conjunto que contém todos os elementos do
conjunto universo U que não pertencem a A.
CA = U − A = { x | x ∈ U e x ∉ A }
A
U

30. Exemplo de Complementar
• Dados os conjuntos A={3, 5} e B={2,3,4,5,6}. Existe
o complementar 𝐶 𝐵
𝐴
, pois A⊂B.
𝑪 𝑩
𝑨
= B − A = {2, 4, 6}.

31. Conjuntos Numéricos

32. Números Naturais ( )
• = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
• * = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
• - Naturais sem o zero.
• Operações em :
• Adição
• Multiplicação

33. Números Inteiros ( )
• = {... -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
• Z* = {... -4, -3, -2, -1, 1, 2, 3, 4, ...}
- Inteiros sem o zero
• Z+ = {0, 1, 2, 3, 4, 5, 6, ...}
• - Inteiros somente com números positivos
• Operações em :
• Adição
• Multiplicação
• Divisão Exata

34. Números Racionais ( )
• São todos aqueles que podem ser expressos na
forma de fração:
= {
𝒂
𝒃
, onde a ∈ Z e b ∈ Z* }

35. Números Irracionais (I)
• Conjunto de números que não podem ser expressos
na forma de uma fração de dois inteiros.
• Decimais infinitos não-periódicos (Inexato).
• Pi =  = 3,14159265358979...
• Raiz quadrada de números primos:
2 = 1,4142 …
I

36. Números Reais (R)
• Conjunto numérico que é a união do conjunto dos
racionais (Q) com os irracionais (I)
• Operações em R:
• Adição e Subtração
• Multiplicação e Divisão