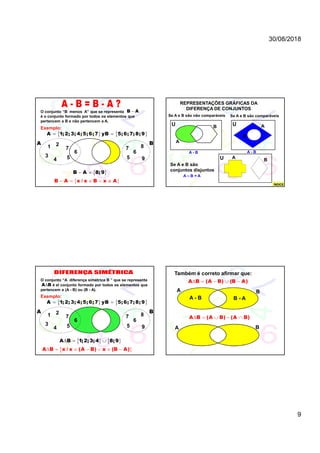
Este documento apresenta os conceitos básicos da teoria de conjuntos, incluindo definições de termos como conjunto, elementos, pertinência, notação de conjuntos, subconjuntos, igualdade de conjuntos, união, interseção e diferença de conjuntos. Explica como representar conjuntos por extensão e entendimento e como diagramas de Venn podem ser usados para ilustrar relações entre conjuntos.

1. 30/08/2018
1
Ensino Superior
Matemática Básica
Unidade 1.1 – Teoria dos Conjuntos
J. Leiitte
INDICE
INTRODUÇÃO
RELAÇÃO DE PERTINÊNCIA
DETERMINAÇÃO DE CONJUNTOS
DIAGRAMAS DE VENN
CONJUNTOS ESPECIAIS
RELAÇÕES ENTRE CONJUNTOS
CONJUNTOS NUMÉRICOS
UNIÃO DE CONJUNTOS
INTERSECÇÃO DE CONJUNTOS
DIFERENÇA DE CONJUNTOS
DIFERENÇA SIMÉTRICA
COMPLEMENTO DE UM CONJUNTO
PROBLEMAS
Em matemática, o conceito de
conjunto é considerado primitivo e
não se dá uma definição deste,
portanto, a palavra CONJUNTO
deve aceitar-se logicamente como
um termo não definido.
Um conjunto se pode entender como
uma coleção ou agrupamento bem
definido de objetos de qualquer classe.
Os objetos que formam um conjunto
são chamados membros ou elementos
do conjunto.
Exemplo:
Na figura ao lado temos
um Conjunto de Pessoas

2. 30/08/2018
2
NOTAÇÃO
Todo conjunto se escreve entre chaves { }
e se denota mediante letras maiúsculas A,
B, C, ..., seus elementos se separam
mediante ponto e vírgula.
Exemplo:
O conjunto das letras do alfabeto; a, b,
c, ..., x, y, z. Se pode escrever assim:
L = {a; b; c; ...; x; y; z}
Exemplo:
A = {a; b; c; d; e} seu cardinal n(A) =
B = {x; x; x; y; y; z} seu cardinal n(B) =
Na teoria de conjuntos não precisa repetir
os elementos, por exemplo:
O conjunto {x; x; x; y; y; z } simplemente
será { x; y; z }.
Ao número de elementos que tem um conjunto
Q chamamos CARDINAL DO CONJUNTO e se
representa por n(Q).
5
3
ÍNDICE
Para indicar que um elemento pertenece a
um conjunto se usa o símbolo: 
Se um elemento não pertenece a um
conjunto se usa o símbolo: 
Exemplo: Seja M = {2; 4; 6; 8; 10}
2 M ... se lê 2 pertenece ao conjunto M
5 M ... se lê 5 não pertenece ao conjunto M
ÍNDICE
I) POR EXTENSÃO
Há duas formas de determinar um conjunto,
por Extensão e por Entendimento.
É aquela forma mediante a qual se indica
cada um dos elementos do conjunto.
Exemplos:
A) O conjunto dos números pares maiores que
5 e menores que 20.
A = { 6; 8; 10; 12; 14; 16; 18 }
ÍNDICE

3. 30/08/2018
3
B) O conjunto de números negativos ímpares
maiores que -10.
B = {-9; -7; -5; -3; -1 }
II) POR ENTENDIMENTO
É aquela forma mediante a qual se dá uma
propriedade que caracteriza a todos os
elementos do conjunto.
Exemplo:
Se pode entender que o conjunto P está formado
pelos números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
P = {os números dígitos }
Outra forma de escrever é: P = { x / x = dígito }
se lê “P é o conjunto formado pelos
elementos x tal que x é um dígito”.
Exemplo:
Expressar por extensão e por entendimento o
conjunto de dias da semana.
Por Extensão: D = {segunda; terça; quarta;
quinta; sexta; sábado; domingo }
Por Entendimento: D = { x / x = dia da semana }
ÍNDICE
Os diagramas de Venn que se devem ao
filósofo inglês John Venn (1834-1883) servem
para representar conjuntos de maneira gráfica
mediante desenhos ou diagramas que podem
ser círculos, retângulos, triângulos ou
qualquer curva fechada.
A
MT
7
2
3
6
9
ae
i
o
u
(1;3) (7;6)
(2;4) (5;8)
84
1 5
ÍNDICE
A = ou A = { } se lê: “A é o conjunto vazio”
ou “A é o conjunto nulo “
CONJUNTO VAZIO
É um conjunto que não tem elementos, também
se chama conjunto nulo. Geralmente se
representa pelos símbolos: ou { }


Exemplos:
M = { números maiores que 9 e menores que 5 }
P = { x / }
1
0
X


4. 30/08/2018
4
CONJUNTO UNITÁRIO
É o conjunto que tem um só elemento.
Exemplos:
F = { x / 2x + 6 = 0 } G =  2
x / x 4 x 0  
CONJUNTO FINITO
É o conjunto com limitado número de
elementos.
Exemplos:
E = { x / x é um número impar positivo
menor que 10 }
N = { x / x2 = 4 }
;
CONJUNTO INFINITO
É o conjunto com ilimitado número de
elementos.
Exemplos:
R = { x / x < 6 } S = { x / x é um número par }
CONJUNTO UNIVERSAL
É um conjunto referencial que contém todos
os elementos de uma situação particular,
geralmente se representa pela letra U
Exemplo:O universo ou conjunto universal
;
de todos os números é o conjunto dos
NÚMEROS COMPLEXOS.
ÍNDICE
INCLUSÃO
Um conjunto A está incluso em outro conjunto B,
se e somente se, todo elemento de A for também
elemento de B.
NOTAÇÃO : A B
Se lê : A está incluso em B, A é subconjunto de B,
A está contido em B , A é parte de B.
REPRESENTAÇÃO GRÁFICA :
B A
PROPRIEDADES:
I) Todo conjunto está incluido em si mesmo. A A
II) O conjunto vazio se considera incluido em
qualquer conjunto.   A
III) A está incluido em B ( ) equivale a dizer
que B contém A ( )
A B
B A
IV) Se A não está incluido em B ou A não é
subconjunto de B significa que pelo menos um
elemento de A não pertence a B. ( )A B
V) Simbolicamente:      A B x A x B

5. 30/08/2018
5
CONJUNTOS COMPARÁVEIS
Um conjunto A é COMPARÁVEL com outro
conjunto B se entre esses conjuntos existe uma
relação de inclusão.
A é comparável com B se A U B = B U A
Exemplo: A = { 1; 2; 3; 4; 5 } e B = { 2; 4 }
1
2
3
4
5
A
B
Observe que B
está incluso em A,
portanto, A e B são
COMPARÁVEIS
IGUALDADE DE CONJUNTOS
Dos conjuntos são iguais se têm os mesmos
elementos.
Exemplo:
A = { x / x2 = 9 } y B = { x / (x – 3)(x + 3) =0 }
Resolvendo a equacão de cada conjunto se obtém
em ambos os casos que x é igual a 3 ou -3, ou
seja: A = {-3; 3} y B = {-3; 3}, portanto A = B
Simbolicamente :     A B (A B) (B A)
CONJUNTOS DISJUNTOS
Dois conjuntos são disjuntos quando não têm
elementos comuns.
REPRESENTACÃO GRÁFICA :
A B
1
7
5 3
9
2
4
8
6



Como podemos
observar os
conjuntos A e B
não têm elementos
comuns, portanto
são CONJUNTOS
DISJUNTOS
CONJUNTO DE CONJUNTOS
É um conjunto cujos elementos são conjuntos.
Exemplo:
F = { {a}; {b}; {a; b}; {a; b; c} }
Observe que os elementos do conjunto F também
são conjuntos.
{a} é um elemento do conjunto F então {a} F
É correto dizer que {b} F ? NÃO
Porque {b} é um elemento do conjunto F, o
correto é {b} F

6. 30/08/2018
6
CONJUNTO POTÊNCIA
O conjunto potência de um conjunto A denotado
por P(A) ou Pot(A) é o conjunto formado por
todos os subconjuntos de A.
Exemplo: Seja A = { m; n; p }
Os subconjuntos de A são:
{m}, {n}, {p}, {m;n}, {n;p},{m;p}, {m;n;p}, Φ
Então o conjunto potência de A é:
P(A) = { {m}; {n}; {p}; {m; n}; {m; p}; {n; p}; {m; n; p}; Φ }
QUANTOS ELEMENTOS TEM O CONJUNTO
POTÊNCIA DE A ?
Observe que o conjunto A tem 3 elementos e seu
conjunto potência ou seja P(A) tem 8 elementos.
PROPRIEDADE:
Dado um conjunto A cujo número de elementos
é n, então o número de elementos de seu
conjunto potência é 2n.
Exemplo:
Dado o conjunto B ={ x / x é um número par e
5 < x < 15 }. Determinar o cardinal de P(B).
RESPOSTA
Se 5 < x < 15 e é um
número par então
B = { 6; 8; 10; 12; 14 }
Observe que o conjunto
B tem 5 elementos então:
Card P(B) = 2n
P(B) = 25 = 32
ÍNDICE
Números Naturais (N) N = {1; 2; 3; 4; 5; ....}
Números Inteiros (Z) Z = {...; -2; -1; 0; 1; 2;....}
Números Racionais (Q)
Q = {...; -2; -1; ; 0; ; ; 1; ; 2; ....}
Números Irracionais ( I ) I = {...; ;....}2; 3; 
Números Reais ( R )
R = {...; -2; -1; 0; 1; ; 2; 3; ....}2; 3
1
2

1
5
1
2
4
3
Números Complexos ( C )
C = {...; -2; ; 0; 1; ; 2 + 3i; 3; ....}2; 3
1
2

N
Z
Q
I
R
C

7. 30/08/2018
7
EXEMPLOS:
Expressar por extensão os seguintes conjuntos:
A )  2
P x N/ x 9 0   
B )
C )
D ) T x Q /(3x 4)(x 2) 0    
E ) B x I/(3x 4)(x 2) 0    
 2
Q x Z / x 9 0   
 2
F x R / x 9 0   
P={3}
Q={-3;3}
F = { }
 
4
T
3

 B 2
RESPOSTAS
INDICE
7
6
55
6
A B
O conjunto “A unão B” que se representa é o
conjunto formado por todos os elementos que
pertenecem a A, a B ou a ambos os conjuntos.
A B
    A B x / x A x B
Exemplo:
  A 1; 2; 3; 4; 5; 6; 7 yB 5; 6; 7; 8; 9
9
87
3
1
4
2
 A B 1;2; 3; 4;5;6;7;8;9
REPRESENTAÇÕES GRÁFICAS DA UNÃO
DE CONJUNTOS
Se A e B são não comparáveis Se A e B são comparáveis
Se A e B são
conjuntos disjuntos
U
U
U
A
A
A
B
B
B
AUB AUB
PROPRIEDADES DA UNIÃO DE
CONJUNTOS
1. A U A = A
2. A U B = B U A
3. A U Φ = A
4. A U U = U
5. (AUB)UC = AU(BUC)
6. Se A U B = Φ  A = Φ e B = Φ
ÍNDICE

8. 30/08/2018
8
7
6
55
6
A B
O conjunto “A intersecção B” que se representa é
o conjunto formado por todos os elementos que
pertencem a A e pertencem a B.
A B
A B x / x A x B    
Exemplo:
  A 1; 2; 3; 4; 5; 6; 7 yB 5; 6; 7; 8; 9
9
87
3
1
4
2
A B 5;6;7 
REPRESENTAÇÕES GRÁFICAS DA
INTERSECÇÃO DE CONJUNTOS
Se A e B são não comparáveis Se A e B são comparáveis
Se A e B são
conjuntos disjuntos
U
U
U
A
A
A B
B
A  B A  B = B
B
A  B = Φ
PROPRIEDADES DA INTERSECÇÃO DE
CONJUNTOS
1. A  A = A
2. A  B = B  A
3. A  Φ = Φ
4. A  U = A
5. (A  B)  C =A (B  C)
6. A U (B  C) =(A U B)  (A U C)
A  (B U C) =(A  B) U (A  C)
ÍNDICE
7
6
55
6
A B
O conjunto “A menos B” que se representa é o
conjunto formado por todos os elementos que pertencem
a A e não pertencem a B.
A B
A B x / x A x B    
Exemplo:
  A 1; 2; 3; 4; 5; 6; 7 yB 5; 6; 7; 8; 9
9
87
3
1
4
2
A B 1;2;3; 4 

9. 30/08/2018
9
7
6
55
6
A B
O conjunto “B menos A” que se representa
é o conjunto formado por todos os elementos que
pertencem a B e não pertencem a A.
B A
B A x / x B x A    
Exemplo:
  A 1; 2; 3; 4; 5; 6; 7 yB 5; 6; 7; 8; 9
9
87
3
1
4
2
B A 8;9 
REPRESENTAÇÕES GRÁFICAS DA
DIFERENÇA DE CONJUNTOS
Se A e B são não comparáveis Se A e B são comparáveis
Se A e B são
conjuntos disjuntos
U
U
U
A
A
A
B
B
A - B A - B
B
A – B = A
ÍNDICE
7
6
55
6
A B
O conjunto “A diferença simétrica B ” que se representa
é el conjunto formado por todos os elementos que
pertencem a (A - B) ou (B - A).
A B
A B x / x (A B) x (B A)      
Exemplo:
  A 1; 2; 3; 4; 5; 6; 7 yB 5; 6; 7; 8; 9
9
87
3
1
4
2
 A B 1;2;3; 4 8;9  
Também é correto afirmar que:
A B (A B) (B A)    
A B (A B) (A B)    
A B
A - B B - A
A B

10. 30/08/2018
10
Dado um conjunto universo U e um conjunto
A, se chama complemento de A ao conjunto
formado por todos os elementos do universo
que não pertencem ao conjunto A.
Notacão: A’ ou AC
Exemplo:
U = {1; 2; 3; 4; 5; 6; 7; 8; 9} A = {1; 3; 5; 7; 9}e
Simbolicamente: A ' x / x U x A   
A’ = U - A
1
2 3
4
5
6
7
8
9
U
AA
A’ = {2; 4; 6; 8}
PROPRIEDADES DO COMPLEMENTO
1. (A’)’ = A
2. A U A’ = U
3. A  A’ = Φ
4. U’ = Φ
5. Φ’ = U
ÍNDICE
PROBLEMA 1
PROBLEMA 2
PROBLEMA 3
PROBLEMA 4
PROBLEMA 5
FIM
Dados os conjuntos:
A = { 1; 4; 7; 10; ... ; 34}
B = { 2; 4; 6; ...; 26}
C = { 3; 7; 11; 15; ...; 31}
a) Expressar B e C por entendimento
b) Calcular: n(B) + n(A)
c) Achar: A  B , C – A
SOLUÇÃO

11. 30/08/2018
11
Os elementos de A são:
Primeiro analisemos cada conjunto
{
1 3x1
tt4tt

{
1 3x2
tt7tt

{
1 3x3
tt tt10

{
1 3x11
tt3 tt4

{
1 3x0
tt1tt

...
A = { 1+3n / nZ / 0  n  11}
Os elementos de B são:
{
2x2
tt4tt {
2x3
tt6tt {
2x4
tt8tt {
2x13
tt tt26{
2x1
tt2tt ...
B = { 2n / nZ / 1  n  13} n(B) = 13
n(A) = 12
Os elementos de C são:
{
3 4x1
tt7tt

{
3 4x2
tt tt11

{
3 4x3
tt tt15

{
3 4x7
tt tt31

{
3 4x0
tt3tt

...
C = { 3 + 4n / nZ / 0  n  7 }
a) Expressar B e C por entendimento
B = { 2n / nZ / 1  n  18}
C = { 3+4n / nZ / 0  n  7 }
b) Calcular: n(B) + n(A)
n(C) = 8
n(B) + n(A) = 13 +12 = 25
A = {1;4;7;10;13;16;19;22;25;28;31;34}
B = {2;4;6;8;10;12;14;16;18;20;22;24;26}
C = {3;7;11;15;19;23;27;31}
c) Achar: A  B , C – A
A  B = { 4; 10; 16; 22 }
C – A = { 3; 11; 15; 23; 27 }
Sabemos que A  B é formado pelos
elementos comuns de A e B, então:
Sabemos que C - A é formado pelos
elementos de C que não pertencem a A,
então:
Se : G = { 1; {3}; 5; {7;10}; 11 }
Determinar se é verdadeiro ou falso:
a) Φ  G
b) {3}  G
c) {{7}; 10}  G
d) {{3}; 1}  G
e) {1; 5; 11}  G
SOLUÇÃO

12. 30/08/2018
12
Observe que os elementos de A são:
1 ; {3} ; 5 ; {7;10} ; 11
es VERDADERO
Então:
é VERDADEIRO porque Φ está
incluso em todos os conjuntos
é VERDADEIRO porque {3}
é um elemento de G
é FALSO porque {{7};10}
não é elemento de G
é FALSO
a) Φ  G ....
b) {3}  G ...
c) {{7}; 10}  G ...
d) {{3}; 1}  G ...
e) {1; 5; 11}  G ...
Dados os conjuntos:
P = { xZ / 2x2 + 5x – 3 = 0 }
M = { x/4N / -4 < x < 21 }
T = { xR / (x2 - 9)(x - 4) = 0 }
a) Calcular: M - ( T – P )
b) Calcular: Pot(M – T )
c) Calcular: (M U T) – P
SOLUÇÃO
P = { xZ / 2x2 + 5x – 3 = 0 }
Analisemos cada conjunto:
2x2 + 5x – 3 = 0
2x – 1
+ 3x


(2x-1)(x+3)=0
2x - 1 = 0  x = 1/2
x + 3 = 0  x = -3
Observe que xZ ,
então: P = { -3 }
M = { x/4N / -4 < x < 21 }
Como x/4  N então os valores de x são: 4; 8;
12; 16; 20 porém os elementos de M se
obtêm dividindo x entre 4, portanto :
M = {1; 2; 3; 4; 5 }
T = { xR / (x2 - 9)(x - 4) = 0 }
Igualamos cada fator a zero e calculamos os
valores de x
x – 4 = 0  x = 4
x2 – 9 = 0  x2 = 9  x = 3 ou x = -3
Portanto: T = { -3; 3; 4 }
a) Calcular: M - ( T – P )
T – P = { -3; 3; 4 } - { -3 }  T – P = {3; 4 }
M - (T – P)= {1; 2 ;3 ;4 ;5 } - {3; 4 }
M - (T – P)= {1; 2; 5 }

13. 30/08/2018
13
b) Calcular: Pot( M – T )
M – T = {1; 2; 3; 4; 5 } - { -3; 3; 4 }
M – T = {1; 2; 5 }
Pot( M – T ) = { {1}; {2}; {5};{1;2};{1;5};
{1;2;5};
{2;5};
Φ }
c) Calcular: (M U T) – P
M U T = {1; 2; 3; 4; 5 } U { -3; 3; 4 }
M U T = { -3; 1 ; 2 ; 3; 4; 5 }
(M U T) – P = { -3; 1; 2; 3; 4; 5 } - { -3 }
(M U T) – P = {1; 2; 3; 4; 5 }
Expressar a região sombreada em
termos de operações entre os
conjuntos A, B e C.
A B
C
A
B
C
SOLUÇÃO
A B
C
A B
C
A
B
C
A
B
C
[(AB) – C]
[(BC) – A]
[(AC) – B]
U U
A B
A
B
C
Observe como se
obtém a região
sombreada
Toda a zona de amarelo é
AUB
A zona de verde é AB
Então, restando se obtém a zona que se
vê na figura: (AUB) - (AB)
C
Finalmente, lhe agregamos C e se obtém:
[ (AUB) - (AB) ] U C ( A  B ) U C=

14. 30/08/2018
14
Segundo as preferências de 420
pessoas que assistem os canais A,
B ou C se observa que 180
assistem o canal A, e 240 assistem o
canal B e 150 não assistem o canal
C, os que assistem pelo menos 2
canais são 230. Quantos assistem
os três canais?
SOLUÇÃO
O universo é: 420
Assistem A: 180 Assistem B: 240
Não assistem C: 150
Então, se assistem o canal C: 420 – 150 = 270
A B
C
a
d
(I) a + e + d + x = 180
be
x
f
(II) b + e + f + x = 240
c
(III) d + c + f + x = 270
Fato: Assistem por lo
menos dos canales 230,
entonces:
(IV) d + e + f + x = 230
(I) a + e + d + x = 180
(II) b + e + f + x = 240
(III) d + c + f + x = 270
Somamos as equações (I), (II) e (III)
Sabemos que: a + b + c + d + e + f + x = 420

230
então: a + b + c = 190
a + b + c + 2(d + e + f + x) + x = 690

190 230
190 + 560 + x =690  x = 40
Isto significa que 40 pessoas assistem os tres canais