1) O documento discute conceitos básicos de conjuntos, incluindo elementos, representação, igualdade, pertinência e subconjuntos.
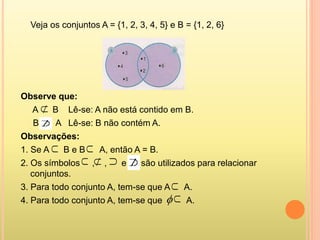
2) Há diferentes formas de representar conjuntos, como lista de elementos, diagrama de Venn e compreensão.
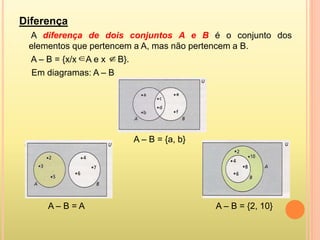
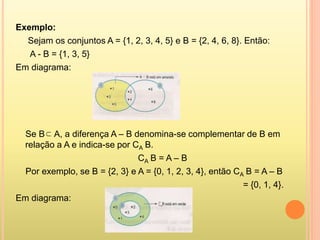
3) Operações com conjuntos como união, interseção e diferença são explicadas com exemplos.