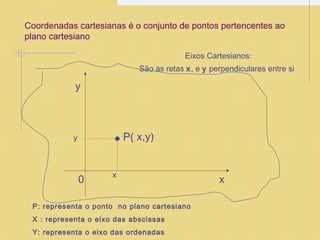
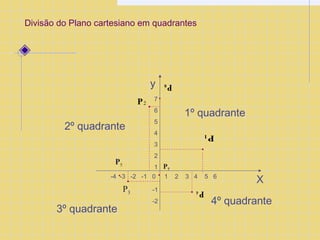
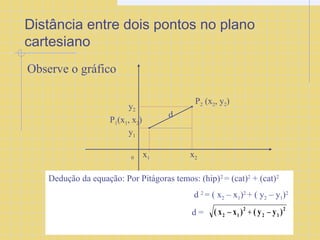
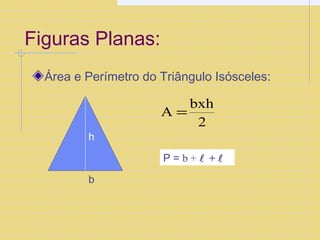
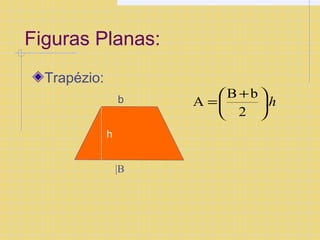
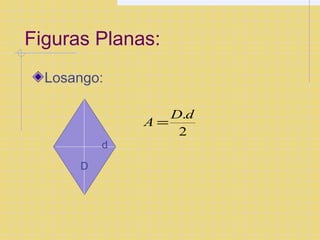
O documento descreve as coordenadas cartesianas, incluindo eixos x e y ortogonais, pontos representados por pares ordenados (x,y), e a divisão do plano cartesiano em quadrantes. Também apresenta fórmulas para calcular distância entre pontos e áreas de figuras planas como quadrado, retângulo e triângulo.

1. Coordenadas Cartesianas
Prof. Elaine Mello

2. Coordenadas cartesianas é o conjunto de pontos pertencentes ao
plano cartesiano
Eixos Cartesianos:
São as retas x, e y perpendiculares entre si
x
y
0
P( x,y)
y
x
P: representa o ponto no plano cartesiano
X : representa o eixo das abscissas
Y: representa o eixo das ordenadas

3. Par ordenado:
O par ordenado é o conjunto constituído de
dois elementos sempre n a mesma ordem (x,y).
x
y
0
P( x,y)
P: representa o ponto no plano cartesiano
X : representa o eixo das abscissas
Y: representa o eixo das ordenadas

4. Par ordenado:
O par ordenado é um conjunto de dois elementos dispostos
na mesma ordem (x,y)
y
7
6
5
4
3
2
1
-3 -2 -1 0 1 2 3 4 5 6
-1
-2
P1
P2
Indicando as coordenadas dos pontos,
no plano:
P3
P4
P1 = ( 4, 2) P2 = (1 , 6) P3 = ( -3,1)
e P4 = (-1, 3)
x

5. Divisão do Plano cartesiano em quadrantes
y
7
6
5
4
3
2
1
2º quadrante
•
P5 P7
-4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
P2
P3 4 P
3º quadrante
X
1º quadrante
4º quadrante
•
P1
P6
•

6. Observação:
Características dos Pares ordenados no
Plano Cartesiano
P1 Î 1º q. Þ (+, +) P5Î X Þ (x, 0)
P2 Î 2º q. Þ (-, +) P6Î Y Þ (0, y)
P3 Î 3º q. Þ (-, -) P7Î X Ç Y Þ(0, 0)
P4 Î 4º q. Þ (+, -)

7. Aplicações:
Construa o plano cartesiano, localize os
pontos dados, una esses pontos e determine a
área e o perímetro da figura formada.
a) P1(5, 0); P2(5, 5); P3(0, 0); P4(0, 5).
b) P1(-2, -2); P2(3, -2); P3(-2, 1).
c) P1(-3, 3); P2(0, 0); P3(-3, 0); P4(0, 3).

8. Distância entre dois pontos no plano
cartesiano
Observe o gráfico
y2
P d 1(x1, x2)
y1
P2 (x2, y2)
0 x1 x2
Dedução da equação: Por Pitágoras temos: (hip)2 = (cat)2 + (cat)2
d 2 = ( x2 – x1)2 + ( y2 – y1)2
d = 2
2 1
2
2 1 ( x – x ) + ( y – y )

9. Exercícios:
Determine a distância entre os pontos
dados:
1. A(-2, 3) e B(-1,-1)
2. A(4, 5) e B( 0, 2)
3. A(2, -6) e B(-1, 0)
4. A(1, 0) e B(-2, 3)
5. A( 5 , 0) e B( 0, 1)

10. Pares ordenados
Igualdade entre pares ordenados:
Dois pares ordenados são iguais quando seus elementos forem
iguais.
Notação: (x, y) = ( a, b) Þ x = a e y = b
Segundo essa afirmação, calcule as variáveis nas igualdades
entre os pares dados:
a) ( 2a + b, 5a – 3b) = (3, 2)
b) (a + 2b, 17) = (6, a + b)
c) (x +y, x – y) = (3, 5)
d) (5x + 2y, 2x + y) = (12, 3)
e) (a2 + a, 4b2 – 1 ) = ( 2, 7)

11. Figuras Planas
Área, Diagonal e Perímetro do quadrado:
A =  x  =
 2
a 2
P = 4 
D =
D

12. Figuras Planas:
Área e Perímetro do Retângulo:
A = b x h
P = 2b + 2h
d h
b

13. Figuras Planas:
Área e Perímetro do Triângulo Isósceles:
h
b
A = bxh
2
P = b + + 

14. Figuras Planas:
Trapézio:
b
|B
h
=æ +
A B b ö ÷ø
çè
h .
2

15. Figuras Planas:
Losango:
A =D.d
2
d
D

16. Atividades: (sugstão, faça no final da
aula)
Calcular a medida da diagonal do quadrado de lado .
Calcular a medida da diagonal de um retângulo de comprimento
e altura .
8 2cm
6 2cm 3 2cm