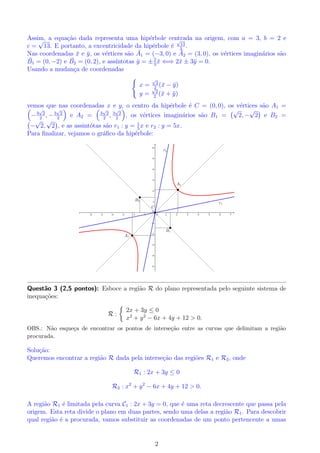
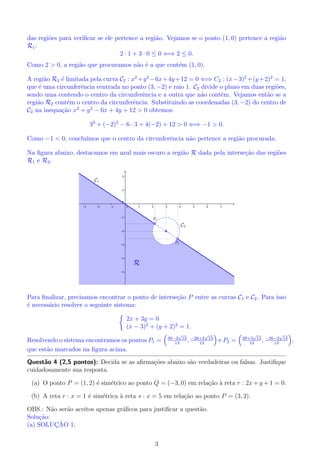
O documento apresenta quatro questões de geometria analítica resolvidas. A primeira questão classifica uma cônica em coordenadas polares como uma parábola e a parametriza. A segunda questão analisa uma hipérbole dada em coordenadas cartesianas, encontrando seus elementos característicos. A terceira questão delineia a região delimitada por dois sistemas de desigualdades. A quarta questão verifica a simetria de pontos em relação a retas e um ponto.

1. Fundac~ao Centro de Ci^encias e Educac~ao Superior a Dist^ancia do Estado do Rio de Janeiro
Centro de Educac~ao Superior a Dist^ancia do Estado do Rio de Janeiro
Gabarito - AP2 { Geometria Analtica I { 2014.2
Quest~ao 1 (2,0 pontos): Considere a c^onica r =
2
1 + sen
dada em coordenadas polares.
(a) Determine a equac~ao da c^onica dada em coordenadas cartesianas e classi

2. que-a como
elipse, hiperbole ou parabola.
(b) Parametrize a c^onica dada.
Soluc~ao:
(a) facil ver que p
a equac~ao dada pode ser escrita da seguinte forma r + r sen = 2. Da,
sabendo que r =
x2 + y2 e y = r sen , temos
E
r + r sen = 2 ()
p
x2 + y2 + y = 2
()
p
x2 + y2 = 2 y
() x2 + y2 = 4 4y + y2
() x2 = 4(y 1):
A equac~ao representa uma parabola com concavidade voltada para a esquerda e vertice (0; 1).
OBS.: N~ao sera cobrada a concavidade e o vertice da parabola.
(b) Fazendo x = t, parametrizamos a parabola do item anterior da seguinte forma:
x = t
y = t2
4 + 1
; t 2 R:
Quest~ao 2 (3,0 pontos): Efetuando uma rotac~ao de 45o nos eixos OX e OY , veri

3. que que
a equac~ao 5x2 26xy + 5y2 + 72 = 0 representa uma hiperbole, encontre seu centro, focos,
vertices (sobre os eixos focal e n~ao focal), assntotas e a excentricidade. Faca tambem o gra

4. co
da hiperbole marcando o centro, focos, vertices e assntotas.
Soluc~ao:
Como
x = x cos y sen
y = x sen + y cos
;
temos (
x =
p
2
2 (x y)
y =
p
2
2 (x + y)
:
Substituindo as equac~oes acima na equac~ao dada obtemos:
5
2
4
(x y)2 26
p
2
2
p
2
2
(x y)(x + y) + 5
2
4
(x + y)2 + 72 = 0;
que pode ser rescrita da seguinte forma:
16x2 + 36y2 + 144 = 0 ()
x2
9
y2
4
= 1: