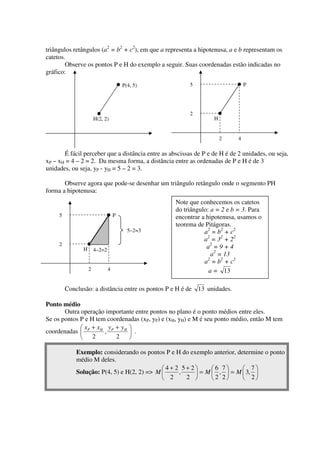
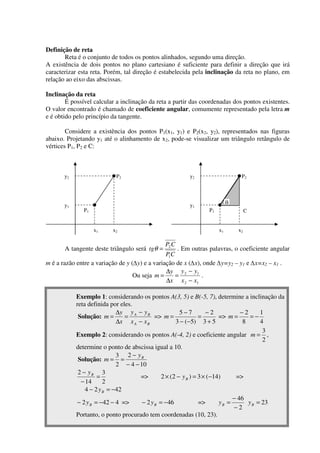
(1) O documento introduz os conceitos básicos de geometria analítica, incluindo o plano cartesiano, pares ordenados, coordenadas de pontos e cálculo da distância entre pontos; (2) Apresenta como calcular a inclinação e equação de uma reta a partir de dois pontos, e como determinar o ponto de interseção entre duas retas.

1. INTRODUÇÃO AO CÁLCULO
“Aprender Cálculo pode ser sua experiência educacional mais
empolgante e estimulante pois é a base para quase toda a Matemática e para
muitas das grandes realizações no mundo moderno”. (Louis Leithold)
RETAS E COORDENADAS
O plano cartesiano
A criação da Geometria Analítica é atribuída a René Descartes (1596-1650) que usou
a técnica do plano numérico (R2) por volta de 1637.
Os eixos x e y
Trata-se da disposição de dois eixos imaginários, dispostos um na vertical (eixo y) e
outro na horizontal (eixo x), sendo chamado de origem o ponto de interseção entre eles.
Pares ordenados
Os eixos x e y foram numerados, a partir da origem, até o infinito. Assim, passou a
existir uma infinidade de combinações entre esses valores, representados por (x, y) = (a, b),
onde x = a e y = b. Por exemplo, se (3, 7) é um par ordenado, então x = 3 e y = 7. Porém, (3,
7) é diferente de (7, 3)
Abscissa e Ordenada
Em um par ordenado, o valor atribuído a x é chamado de abscissa e o valor atribuído a
y é chamado de ordenada.
Coordenadas de um ponto
Na Geometria Analítica, cada par ordenado é associado a um ponto imaginário no
plano cartesiano. É representado por uma letra maiúscula seguida do par ordenado. Exemplo:
P(5, -3) é um ponto associado ao par ordenado (x, y) = (5, -3).
Um ponto P(x, y) é representado no plano cartesiano conforme o exemplo:
Quadrantes:
P(4, 2)
M(-2, 2) O plano cartesiano é dividido
em quatro quadrantes:
0, 0 P está no quadrante I
M está no quadrante II
L(-5, -1)
L está no quadrante III
H está no quadrante IV
H(2, -3)
Distância entre dois pontos
Já que supomos a existência de um ponto imaginário no plano cartesiano, é natural que
existam outros, pois a possibilidade de pares ordenados é infinita. Entre dois pontos, a
primeira pergunta a se fazer é “qual a distância entre eles?”. A Geometria Analítica responde
a esta questão usando uma fórmula simples baseada no Teorema de Pitágoras aplicado em

2. triângulos retângulos (a2 = b2 + c2), em que a representa a hipotenusa, a e b representam os
catetos.
Observe os pontos P e H do exemplo a seguir. Suas coordenadas estão indicadas no
gráfico:
P(4, 5) 5 P
2
H(2, 2) H
2 4
É fácil perceber que a distância entre as abscissas de P e de H é de 2 unidades, ou seja,
xP – xH = 4 – 2 = 2. Da mesma forma, a distância entre as ordenadas de P e H é de 3
unidades, ou seja, yP - yH = 5 – 2 = 3.
Observe agora que pode-se desenhar um triângulo retângulo onde o segmento PH
forma a hipotenusa:
Note que conhecemos os catetos
do triângulo: a = 2 e b = 3. Para
5 P encontrar a hipotenusa, usamos o
teorema de Pitágoras.
5–2=3 a2 = b2 + c2
a2 = 32 + 22
2 a2 = 9 + 4
H 4–2=2
a2 = 13
a2 = b2 + c2
2 4 a = 13
Conclusão: a distância entre os pontos P e H é de 13 unidades.
Ponto médio
Outra operação importante entre pontos no plano é o ponto médios entre eles.
Se os pontos P e H tem coordenadas (xP, yP) e (xH, yH) e M é seu ponto médio, então M tem
 x + xH y P + y H 
coordenadas  P ,  .
 2 2 
Exemplo: considerando os pontos P e H do exemplo anterior, determine o ponto
médio M deles.
4+ 2 5+ 2 6 7  7
Solução: P(4, 5) e H(2, 2) => M  ,  = M  ,  = M  3, 
 2 2  2 2  2

3. Definição de reta
Reta é o conjunto de todos os pontos alinhados, segundo uma direção.
A existência de dois pontos no plano cartesiano é suficiente para definir a direção que irá
caracterizar esta reta. Porém, tal direção é estabelecida pela inclinação da reta no plano, em
relação ao eixo das abscissas.
Inclinação da reta
É possível calcular a inclinação da reta a partir das coordenadas dos pontos existentes.
O valor encontrado é chamado de coeficiente angular, comumente representado pela letra m
e é obtido pelo princípio da tangente.
Considere a existência dos pontos P1(x1, y1) e P2(x2, y2), representados nas figuras
abaixo. Projetando y1 até o alinhamento de x2, pode-se visualizar um triângulo retângulo de
vértices P1, P2 e C:
y2 P2 y2 P2
y1 y1 θ
P1 P1 C
x1 x2 x1 x2
P2 C
A tangente deste triângulo será tgθ = . Em outras palavras, o coeficiente angular
P1C
m é a razão entre a variação de y ( y) e a variação de x ( x), onde y=y2 – y1 e x=x2 – x1 .
∆y y 2 − y1
Ou seja m = = .
∆x x 2 − x1
Exemplo 1: considerando os pontos A(3, 5) e B(-5, 7), determine a inclinação da
reta definida por eles.
∆y y A − y B 5−7 −2 −2 1
Solução: m = = => m = = => m = =−
∆x x A − x B 3 − (−5) 3 + 5 8 4
3
Exemplo 2: considerando os pontos A(-4, 2) e coeficiente angular m = ,
2
determine o ponto de abscissa igual a 10.
3 2 − yB
Solução: m = =
2 − 4 − 10
2 − yB 3
= => 2 × (2 − y B ) = 3 × (−14) =>
− 14 2
4 − 2 y B = −42
− 46
− 2 y B = −42 − 4 => − 2 y B = −46 => yB = y B = 23
−2
Portanto, o ponto procurado tem coordenadas (10, 23).

4. Equação da reta
Em Geometria Analítica, os “lugares geométricos” são expressos matematicamente na
forma de equação. A maneira como se apresenta esta equação pode variar conforme a
conveniência, para facilitar o desenvolvimento algébrico.
A forma mais comum é a reduzida: y = mx + b. Onde m é o coeficiente angular e b é
o coeficiente linear.
Como já foi dito, o coeficiente angular representa a inclinação (ou declividade) de uma
reta. Por sua vez, o coeficiente linear mostra o ponto onde a reta intercepta o eixo das
ordenadas.
A partir de dois pontos se pode determinar a equação de uma reta, identificando cada
um de seus elementos.
Exemplo: Dados os pontos A(-3, 7) e B(2, -8), determine a equação da reta
definida por eles.
Solução: Sabe-se que a forma reduzida é y = mx + b. Primeiramente calcula-se o
valor de m.
∆y y A − y B 7 − (−8) 7 + 8 15
m= = => m = = => m = = −3
∆x x A − x B −3−2 −5 −5
Substitui-se m = -5 na forma reduzida:
y = -3x + b.
Substituem-se as coordenadas de qualquer um dos pontos dados, por exemplo, A(-
3, 7) na forma reduzida:
7 = -3(-3) + b.
Logo, desenvolvendo a última expressão, b = -2.
Então se pode escrever a equação y = -3x -2 como a reta que contém os pontos A(-
3, 7) e B(2, -8).
Observação: Uma forma prática de verificar se a equação está correta é substituir o
outro ponto – no caso B(2, -8); na equação:
y = -3x -2 => -8 = -3(2) -2 => -8 = -6 -2 => -8 = -8 (Verdadeiro).
Forma geral da reta
Outra forma de se apresentar uma equação de reta é a forma geral: Ax + By + C = 0;
A C
onde − é o coeficiente angular (m) e − é o coeficiente linear (b), ambos já mostrados.
B B
A C − Ax − C
Na verdade, o que mudou foi a apresentação: y = mx + b => y = − x − => y =
B B B
=> By = − Ax − C => Ax + By + C = 0 .
No estudo inicial de cálculo, a forma geral da reta não representa relevância.
Interceptos
Chamam-se interceptos os valores pelos quais uma reta intercepta os eixos das
abscissas ou das ordenas. O intercepto das ordenadas é o próprio coeficiente linear (b). O
−b
intercepto das abscissas é dado por .
m
Retas paralelas

5. Duas retas em um plano são paralelas quando possuem a mesma inclinação, ou seja,
mesmos coeficientes angulares, mesma declividade.
Outra maneira de verificar se duas retas são paralelas, conhecendo suas equações,
atribui-se duas abscissas (ou duas ordenadas) às duas retas, gerando quatro pontos. Os pontos
de mesma abscissa (ou mesma ordenada) distanciam-se em mesmo valor que os outros dois
pontos. Caso a distância seja nula, trata-se de retas coincidentes.
Retas perpendiculares
Duas retas são perpendiculares se o coeficiente angular de uma é o inverso do oposto
−1
do coeficiente angular da outra. Ou seja: m1 = ou m1 m 2 = −1 .
m2
Exemplo: Sejam as retas l1: 2x – 3y = 12 e l2: 3x + 2y = 4. Verifique se elas são
perpendiculares.
A 2 2
Solução: Coeficiente angular de l1 m1 = − 1 = − =
B1 −3 3
3
−
A 3
Coeficiente angular de l2 m2 = − 2 = − 2 = −
B2 1 2
2 −3
Note que m1 m 2 = × = −1 , portanto l1 e l2 são perpendiculares.
3 2
Pontos de interseção
Duas retas concorrentes, perpendiculares ou não, possuem um único ponto de
interseção. Para determinar esse ponto a partir das equações das retas, basta isolar
simultaneamente uma variável comum.
Exemplo: Sejam as retas l1: x + 2y = 10 e l2: –2x + y = –10.
Determine o ponto de interseção.
Solução: l1: x + 2y = 10 l2: –2x + y = –10
x = 10 – 2y –2x = –10 –y
− 10 − y
x=
−2
Fazendo l1 = l2, vem:
− 10 − y
10 − 2 y = ⇒
−2
− 2(10 − 2 y ) = −10 − y ⇒
− 20 + 4 y = −10 − y ⇒
4 y + y = −10 + 20 ⇒
5 y = 10 ⇒ y = 2
Como y = 2: x = 10 – 2y
x = 10 – 2.2
x = 10 – 4
x=6
Portanto, as retas l1 e l2 se interceptam em (6, 2).