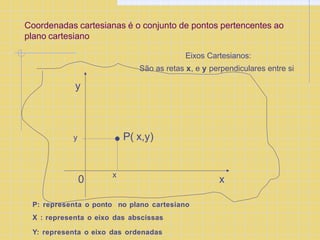
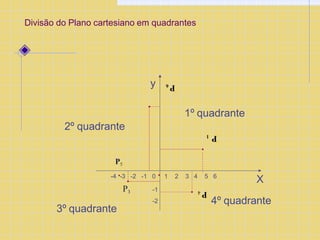
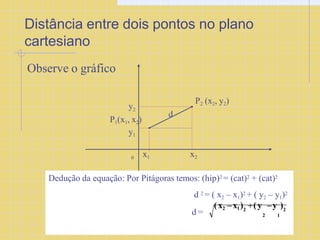
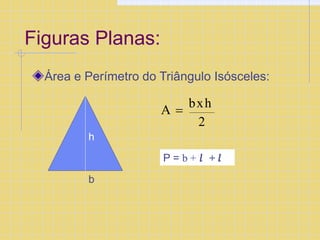
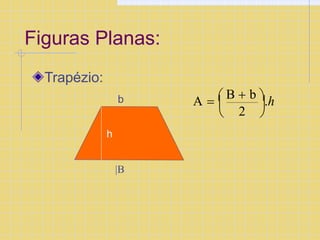
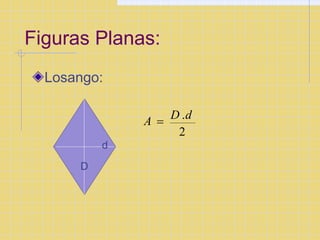
O documento explica os conceitos básicos de coordenadas cartesianas, incluindo eixos x e y, pares ordenados (x,y), quadrantes do plano cartesiano, e fórmulas para calcular distância entre pontos e áreas de figuras geométricas como retângulos, quadrados e triângulos.

1. Coordenadas Cartesianas

2. Coordenadas cartesianas é o conjunto de pontos pertencentes ao
plano cartesiano
Eixos Cartesianos:
São as retas x, e y perpendiculares entre si
x
y
0
P( x,y)
P: representa o ponto no plano cartesiano
X : representa o eixo das abscissas
Y: representa o eixo das ordenadas
y
x

3. x
O par ordenado é o conjunto constituído de
dois elementos sempre na mesma ordem (x,y).
y
P( x,y)
0
P: representa o ponto no plano cartesiano
X : representa o eixo das abscissas
Y: representa o eixo das ordenadas
Par ordenado:

4. Par ordenado:
O par ordenado é um conjunto de dois elementos dispostos
na mesma ordem (x,y)
y
-3 -2 -1 0 1 2 3 4 5 6
7
6
5
4
3
2
1
-1
-2
P
1
P2
Indicando as coordenadas dos pontos,
P3
P
4
x
no plano:
P1 = ( 4, 2) P2 = (1, 6) P3 = ( -3,1)
e P4 = (-1, 3)

5. Divisão do Plano cartesiano em quadrantes
-1
-2
P3 P
4
3º quadrante
X
y
1º quadrante
2º quadrante
4º quadrante
-2 -1 0 • 1 2 3 4 5 6
P5
P
1
P
6
-4 •-3

6. Observação:
Características dos Pares ordenados no
Plano Cartesiano
P1 1º q.  (+, +) P5 X  (x, 0)
P2 2º q.  (, +) P6 Y  (0, y)
P3 3º q.  (, ) P7 X  Y (0, 0)
P4 4º q.  (+, )

7. Aplicações:
Construa o plano cartesiano, localize os
pontos dados, una esses pontos e determine a
área e o perímetro da figura formada.
a) P1(5, 0); P2(5, 5); P3(0, 0); P4(0, 5).
b) P1(-2, -2); P2(3, -2); P3(-2, 1).
c) P1(-3, 3); P2(0, 0); P3(-3, 0); P4(0, 3).

8. Distância entre dois pontos no plano
cartesiano
Observe o gráfico
0 x1 x2
y2
y1
P2 (x2, y2)
d
P1(x1, x2)
Dedução da equação: Por Pitágoras temos: (hip)2 = (cat)2 + (cat)2
d 2 = ( x2 – x1)2 + ( y2 – y1)2
d =
(x2 –x1) (y –y )
2 2
2 1

9. Exercícios:
Determine a distância entre os pontos
dados:
1. A(-2, 3) e B(-1,-1)
2. A(4, 5) e B( 0, 2)
3. A(2, -6) e B(-1, 0)
4. A(1, 0) e B(-2, 3)
5. A( 5, 0) e B( 0, 1)

10. Pares ordenados
Igualdade entre pares ordenados:
Dois pares ordenados são iguais quando seus elementos forem
iguais.
Notação: (x, y) = ( a, b)  x = a e y = b
Segundo essa afirmação, calcule as variáveis nas igualdades
entre os pares dados:
a) ( 2a + b, 5a – 3b) = (3, 2)
b) (a + 2b, 17) = (6, a + b)
c) (x +y, x – y) = (3, 5)
d) (5x + 2y, 2x + y) = (12, 3)
e) (a2 + a, 4b2– 1 ) = ( 2, 7)

11. Figuras Planas
Área, Diagonal e Perímetro do quadrado:
A = 𝑙 x 𝑙 =
𝑙 2
P = 4
a𝑙2
D =
D

12. Figuras Planas:
Área e Perímetro do Retângulo:
A = b x h
P = 2b + 2h
b
h
d

13. Figuras Planas:
Área e Perímetro do Triângulo Isósceles:
A 
bxh
2
h
P = b + 𝑙 + 𝑙
b

14. Figuras Planas:
Trapézio:
b
h
|B
2 
 

A   B  b .h

15. Figuras Planas:
Losango:
A 
D .d
2
d
D

16. Atividades: (sugstão, faça no final da
aula)
Calcular a medida da diagonal de um retângulo de comprimento
2cm .
Calcular a medida da diagonal do quadrado de lado8
3 2cm.
2cme altura
6