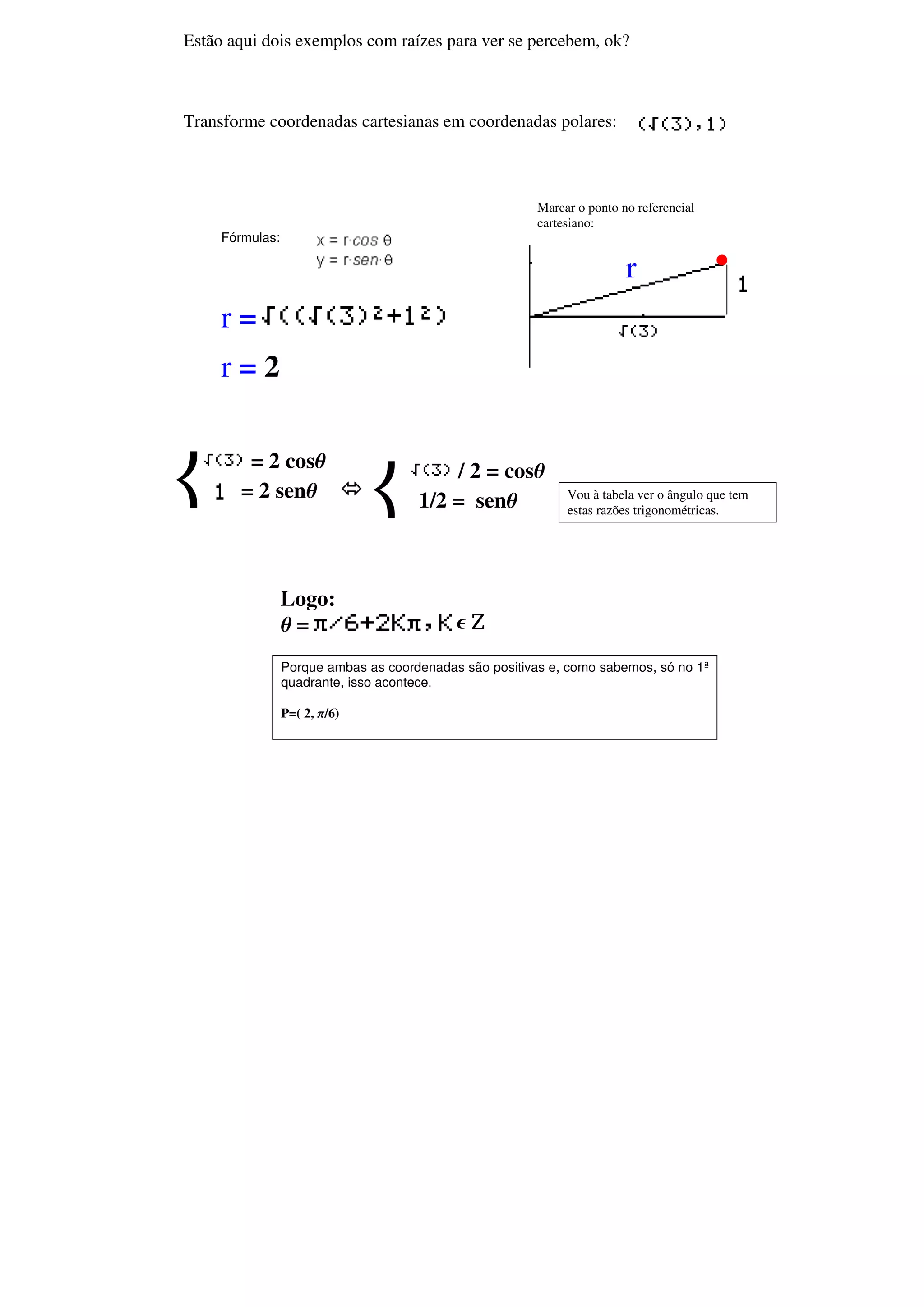
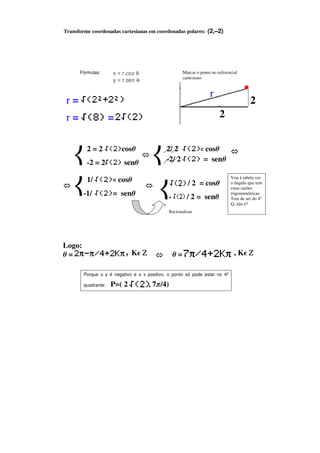
1) O documento apresenta exemplos de transformação de coordenadas cartesianas em coordenadas polares. 2) A primeira transformação envolve o ponto (2, 1/2), que corresponde às coordenadas polares (2, π/6). 3) A segunda transformação envolve o ponto (2, -2), que corresponde às coordenadas polares (2, 7π/4).

1. Estão aqui dois exemplos com raízes para ver se percebem, ok?
Transforme coordenadas cartesianas em coordenadas polares:
Marcar o ponto no referencial
cartesiano:
Fórmulas:
r
r=
r=2
Ó = 2 cosq
= 2 senq
Ó / 2 = cosq
1/2 = senq Vou à tabela ver o ângulo que tem
estas razões trigonométricas.
Logo:
q= eZ
Porque ambas as coordenadas são positivas e, como sabemos, só no 1ª
quadrante, isso acontece.
P=( 2, p/6)

2. Transforme coordenadas cartesianas em coordenadas polares: (2,–2)
Fórmulas: Marcar o ponto no referencial
cartesiano:
r
r= 2
r= = 2
Ó 2=2
-2 = 2
cosq
senq Ó 2/ 2
-2/ 2
= cosq
= senq
Ó Ó
Vou à tabela ver
1/ = cosq / / 2 = cosq o ângulo que tem
estas razões
-1/ = senq - / 2 = senq
trigonométricas.
Tem de ser do 4º
Q, não é?
Racionalizar
Logo:
q= Ke Z q= , Ke Z
Porque o y é negativo e o x positivo, o ponto só pode estar no 4º
quadrante: P=( 2 , 7p/4)