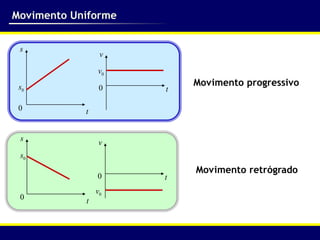
O documento descreve o movimento uniforme, definindo-o como aquele em que a velocidade é constante. Apresenta a função horária da posição S=S0+V*t para descrever o movimento uniforme progressivo ou regressivo, dependendo do sinal da velocidade. Explica como analisar gráficos de posição versus tempo para determinar a velocidade e variação de espaço em intervalos de tempo.

1. CINEMÁTICA
MOVIMENTO UNIFORME

2. Movimento Uniforme
É o movimento onde a velocidade é constante
No movimento uniforme, o corpo percorre distancias
iguais em tempos iguais.

3. Movimento Uniforme
Se a posição do corpo aumenta temos que:
Se a posição do corpo diminui temos que:

4. Movimento Uniforme
Função horária da Posição
S0 S
Ela nos fornece a
posição S em função
do tempo.
s  s0  v.t

5. Movimento Uniforme
Vejamos um exemplo:
V = 5m/s
S0 = 2m
A função horária deste movimento é:
S = 2 + 5.t
E como a velocidade é positiva o movimento é
progressivo

6. Movimento Uniforme
Analisemos a seguinte situação:
Dois corpos A e B estão em movimento com as
respectivas funções horárias
SA = 5 + 2.t e SB = 10 – 3.t
Comparando com S = S0 + V.t podemos afirmar que:
O corpo A está na O corpo B está na
posição inicial de 5m, posição inicial de 10m,
possui uma velocidade possui uma velocidade
de 2m/s e executa um de -3m/s e executa um
movimento progressivo movimento regressivo

7. Sistema de Eixos Cartesianos Ortogonais
• Os valores das grandezas envolvidas são colocados utilizando uma escala
adequada para cada eixo.
• O eixo na horizontal (por convenção) é denominado eixo das abcissas e
nele são colocadas os valores da variável independente (por exemplo,
tempo).
• O eixo na vertical é denominado eixo das ordenadas e nele são colocados
os valores da variável dependente (por exemplo, espaço).

8. Movimento Uniforme
s
v
v0
s0 0
Movimento progressivo
t
0 t
s
v
s0
Movimento retrógrado
0 t
v0
0 t

9. • O gráfico serve para visualizar o comportamento das grandezas físicas
envolvidas de uma maneira fácil e rápida.
• Através de um gráfico podemos verificar como varia uma grandeza (por
exemplo, espaço) em função de outra (por exemplo, tempo).
• A velocidade escalar é obtida a partir do gráfico S versus t,
calculando a inclinação da reta:
V = Inclinação da reta = ΔS / Δt
• Pode-se calcular a variação de espaço ocorrida em um intervalo
de tempo, calculando-se a área abaixo da reta obtida (área
hachurada), que é a área de um retângulo.
ΔS = Area do retângulo = base x altura = Δt x V