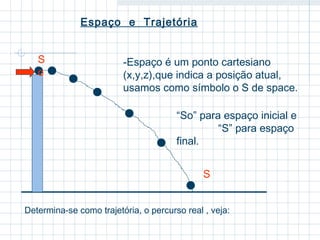
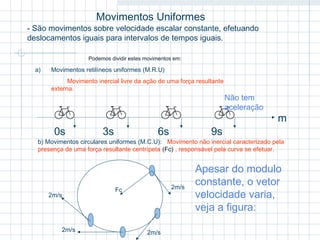
1) O documento discute conceitos básicos da física clássica como repouso, movimento, referencial inercial e extensão relativa de corpos. 2) É explicado que para determinar se um corpo está em repouso ou movimento é necessário um referencial de comparação e que a velocidade deve ser menor que a da luz. 3) São definidos conceitos como referencial inercial, corpo pontual, corpo extenso, movimento, repouso, deslocamento e trajetória.

1. Esta é uma parte da física clássica, onde caracterizamos
e classificamos um possível estado de movimento ou repouso de
um objeto observado, mas sem se preocupar com o(s) porquê(s)
de este objeto, se encontrar nesta atual condição.

2. Para dizermos que um corpo está
em repouso, ou movimento é necessário a
ajuda de um referencial inercial, que pode ser
um ponto espacial, ou outro objeto qualquer
nas proximidades do evento físico.
É importante ressaltar, que se há
movimento, este deve ser bem menor que a
velocidade da luz, senão a relatividade é
moderna.

3. Extensão relativa de um corpo:
Você é grande ou pequeno, gordo ou magro? E o seu pai?
- Este tipo de questionamento é comum quando estamos nos
conhecendo, e relacionando as extensões de tudo que conhecemos.
Mas isto é feito durante muitos anos por nos, usando a si
próprio para relacionar as extensões, e a física exige que você comece
a utilizar outros referenciais que não seja você mesmo, classificando o
objeto observado por corpo pontual (partícula) ou extenso.
A Terra é um corpo partícula em
relação ao Sol.
As xícaras são corpos extensos
em relação ao bule.

4. Movimento e repouso relativos:
-Para se dizer se um corpo se move ou está em repouso,
escolha um referencial, observando se ao passar do tempo a
distância entre o objeto observado e o ponto referencial variou ou
se manteve constante.
A casa esta em repouso em relação ao homem, mas o
carro esta por outro lado em movimento.

5. Definindo:
1- Referencial inercial: Ponto espacial adotado que
pode ser considerado em repouso ou movimento retilíneo uniforme.
2- Corpo pontual:Objeto cujas medidas das
proporções é irrelevante .
3- Corpo extenso:Objeto cuja medidas das produções
são relevantes no raciocínio e calculo físico.
4- Movimento: A distância entre o ponto referencial e o
objeto varia de valor.
5-Repouso: a distância entre o ponto referencial e o
objeto permanece constante ao passar do tempo.

6. Espaço e Trajetória
S
So
-Espaço é um ponto cartesiano
(x,y,z),que indica a posição atual,
usamos como símbolo o S de space.
“So” para espaço inicial e
“S” para espaço
final.
Determina-se como trajetória, o percurso real , veja:

7. Quando ocorre uma variação nas posições ou espaços (DS =
deslocamento), devemos primeiramente verificar o sistema métrico
que esta sendo utilizado e em segundo lugar o seu modulo, efetuando
o seguinte procedimento matemático.
DS = S -
ExemploS: o
-2m 0 2m 4m 8m
(m)
Entenda a figura, como um objeto que se move, de
acordo com o sentido indicado do trajeto.
a) Quanto deslocou ao total, de acordo com a figura, a pequena bolinha?
DS= S-So = 8 – (-2) = 10m
b) Qual foi o deslocamento efetuado da posição –2m até 4m?
DS= S-So = 4 – (-2) = 6m
Obs:É comum chamar a posição zero de
origem dos espaços.

8. - Grandeza física mista,
que mede a rapidez que
se efetua um
deslocamento, por
unidade de tempo.
Quando a velocidade é medida através de
um velocímetro, dizemos que ela é
instantânea.
.0(s) Quando existe um movimento qualquer, e ponderamos seu
deslocamento (DS) por intervalo de tempo que ocorreu (Dt).
.....20m..2(s)
........60m.........6(s)
Estamos determinando uma velocidade média
para este movimento.
Vm = DS
Dt
Exemplo:
Vm = DS = 60 = 10(m/s)
Dt 6

9.  Quando um móvel variou sua velocidade
(DV) por um intervalo de tempo (Dt),
dizemos que este sofreu uma:
A aceleração também é uma grandeza física mista, podendo ser
instantânea (a) ou média (Am)(feita por média ponderada).
-Por motivos da atual grade curricular do novo ensino médio, apenas trabalhamos com
movimentos uniformes variados, logo o modulo da aceleração instantânea e média,
são “sempre” idênticos.
a = Am = DV
Dt
Para uma mesma desaceleração, um veiculo leva espaços maiores para parar quando a
velocidade é maior.

10. Exemplo:Qual a aceleração média de um movimento uniforme variado, de acordo
com a tabela de valores abaixo:
m/s 24 20 16 12
s 0 2 4 6
Am = DV : Dt = (12 – 24):( 6 – 0)= -12 : 6= -2(m/s 2)
Obs: Para normas internacionais de
sistemas métricos, exige-se o uso de
m/s para velocidade e m/s2 para
aceleração

11. 1. U. Católica-DF Para buscar um vestido, Linda tem que percorrer uma distância total de
10 km, assim distribuída: nos 2 km iniciais, devido aos sinaleiros e quebra-molas, determinou
que poderia gastar 3 minutos. Nos próximos 5 km, supondo pista livre, gastará 3
minutos. No percurso restante mais 6 minutos, já que se trata de um caminho com ruas
muito estreitas.
Se os tempos previstos por Linda forem rigorosamente cumpridos, qual será sua velocidade
média ao longo de todo o percurso?
a) 50 km/h d) 11 m/s
b) 1,2 km/h e) 60 km/h
c) 20 m/s
Vm = DS = 2+5+3(Km)
Dt 3+3+6(min)
= 10(km)
0,2(h)
= 50 Km/h
Obs: 12(min)..... :60...= 0,2(h)
Letra a
Obs: Temos um movimento
uniforme progressivo, porque
V>0.

12. 2-U.E. Londrina-PR Um pequeno animal desloca-se com velocidade média igual a 0,5 m/s.
A velocidade desse animal em km/dia é:
a) 13,8 b) 48,3 c) 43,2 d) 1,80 e) 4,30
Primeiro faça isto;
m ...... :1000..... = 1/1000Km
S ..... :3600.. = 1/3600 h .... : 24... = 1/86400 dias
Substituindo:
0,5m =
s
1(km)
0,5 x1000 = 0,5x 86400 = 43,2 (km/dia)
1(dias) 1000
86400

13. Movimentos Uniformes
- São movimentos sobre velocidade escalar constante, efetuando
deslocamentos iguais para intervalos de tempos iguais.
Podemos dividir estes movimentos em:
a) Movimentos retilíneos uniformes (M.R.U)
Movimento inercial livre da ação de uma força resultante
externa.
Não tem
 


aceleração
m
0s
3s
6s
9s
b) Movimentos circulares uniformes (M.C.U): Movimento não inercial caracterizado pela
presença de uma força resultante centrípeta (Fc) , responsável pela curva se efetuar.
Fc 2m/s
2m/s
2m/s 2m/s
Apesar do modulo
constante, o vetor
velocidade varia,
veja a figura:

14. De forma bem geral, devido a velocidade escalar constante,
Galileu observou e constatou que todos movimentos uniformes podem ser
descritos suas posições em função do tempo, por uma função do 1° grau.
S = So + V.T
Caso a velocidade escalar sofra mudança em seu
modulo, devemos mudar a classificação do movimento para
variado pois esta embutido nesta mudança do fenômeno
dinâmico uma aceleração tangencial que pode ser constante,
como veremos já na próxima pagina.

15. Função horária da velocidade:
a = V – Vo
DT
V – Vo = a .DT
V = Vo + a .DT
Uma função do 1° grau como f(x)= aX + b , onde Vo (velocidade inicial) é
o coeficiente linear, lembra? Aquele numero onde o gráfico corta o eixo
“Y” , e a aceleração como coeficiente angular. Vejamos:
V
t
V1
VoT1
T2
V2
q
Tg q = DV = a
DT

16. Exemplo: De acordo com o diagrama abaixo, caracterise os tipos
de movimentos uniformes variados presentes.
V
t
to t1 t2 t3
t4
Vamos analisar:
Sintetizando:
De to à t1, temos v>0 e a>0 , logo um movimento uniforme progressivo
aDceel et1ra àd ot2. , temos V>0 e a<0, logo um movimento uniforme progressivo
retardado.
Quando V>0 , o movimento é progressivo , e quando V<0 , o movimento é
retrogrado. Analisando a velocidade juntamente com a aceleração, se ambos tiverem o
mesmo sinal , trata-se de uma aceleração, caso contrario dizemos que houve um
retardamento(desaceleração).
De t2 à t3, temos V<0 e a<0, logo um movimento uniforme retrogrado
acelerado.
De t3 à t4, temos V<0 e a>0, logo um movimento uniforme retrogrado retardado.

17. Exercício 03: Um objeto qualquer é deixado cair do vigésimo andar sobre ação unida da
aceleração da gravidade (g=10m/s2 ) , levando 0,3min para chegar ao chão. Podemos dizer
que a velocidade ao chegar ao solo será de:
x
a)3m/s b) –3m/s c) 180m/s d) –180m/s e) n.d.a
Resolução:
V = Vo + a . t V= 0 + 10.18 Vo=0, porque é deixado cair
e 0,3min x60= 18s
V= 180m/s

18. Função horária da posição para o M.U.V
V
T
- Quando calculamos a área de um polígono, de
certa forma acabamos sempre multiplicando a base
da figura pela altura. Fazendo assim uma analogia
com a figura formada no diagrama VxT o produto
da velocidade por intervalo de tempo, de forma
integral , corresponde ao deslocamento, logo ao
modulo da área da figura.
to
V
t
V.dt = |área| = deslocamento (DS)
|área de um trapézio|= DS S – So = (V – Vo).t
2
t
Vo
(B+b).h = área de um trapézio
2
V- Vo = a .t
S = So + Vo.t + a . T 2
2

19. Exemplo: Um móvel percorre um trajeto de acordo com a função S= 8t + 2t 2 em
S.I.
a) Qual a posição inicial, velocidade inicial e aceleração de acordo com a função:
R: Comparando com S = So + Vo.t + a/2 . T 2
So=0; V0=8m/s; a/2= 2, logo a=4m/s 2.
b) Classifique o movimento quanto a velocidade e aceleração:
R: Movimento uniforme progressivo acelerado
c) Monte a função horária da velocidade para este movimento:
R: V = Vo + a .t
V = 8 + 4.t
d) Monte um diagrama SxT para a função:
S t
0 0
S = 8.0+ 2.02
S =0
10 1
8.1 + 2. 12
S = 10m
24 2
S = 8.2 + 2.22
S = 24m
S
t
1 2
22
10

20. Equação de Torricelli:
Evangelista Torricelli, aluno
de Galileu, montou através
das funções de seu mestre
uma equação baseada em
um movimento uniforme
variado, sem haver
dependência temporal.
Substituindo V = Vo + at
em S=So + Vo.t +a/2.t2
V2 = Vo2 + 2.a.
DS
Exemplo: Partindo do repouso, um
veiculo com aceleração constante de
1m/s2 chega ao final de uma ponte
com 20m/s de velocidade.Qual deverá
ser a extensão da ponte para que isto
ocorra?
V2 = Vo2 + 2.a. DS
202 = 0 + 2. 1.
DS
DS = 400 : 2 = 200m
Achou:

21. Exercício: 04. (Mackenzie)Do alto de um edifício, lança-se horizontalmente uma pequena
esfera de chumbo com velocidade de 8m/s. Essa esfera toca
o solo horizontal a uma distância de 24m da base do prédio, em relação à vertical que passa pelo
ponto de lançamento.
Desprezando a resistência do ar, a altura desse prédio é: (Adote g = 10m/s2)
a) 45m b) 40m c) 35m d) 30m e) 20m
R:
As equações da ordenada (y) e da abscissa (x) da esfera são:
y = 5t2 e x = 8t
Quando a esfera atinge o solo, temos:
24 = 8t t = 3s.
Portanto, a altura (h) do prédio é: h = 5 . 32 h = 45m
X

22. -Em uma prova de 100 m rasos, o desempenho típico de um corredor padrão
é representado pelo gráfico a seguir:
12
10
8
6
4
2
0
0 2 4 6 8 10 12 14 16
Tempo (s)
Velocidade (m/s)
Exercício:05.(Enem1998) Baseado no gráfico, em que intervalo de tempo a velocidade do corredor é
aproximadamente constante?
(A) Entre 0 e 1 segundo.
R: Quando o gráfico for praticamente uma reta
(B) Entre 1 e 5 segundos.
horizontal.
(C) Entre 5 e 8 segundos.
(D) Entre 8 e 11 segundos.
(E) Entre 12 e 15 segundos.
X