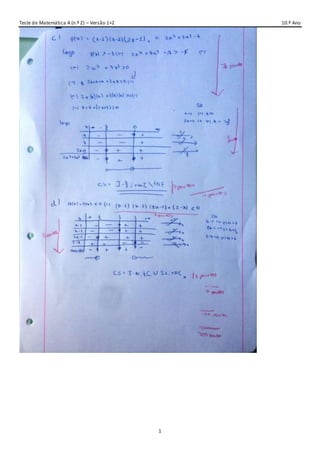
O documento é um teste de matemática para o 10.o ano, abordando temas de geometria e álgebra, incluindo radicais e polinômios. Ele é dividido em dois grupos, com questões de escolha múltipla e desenvolvimento, requerendo cálculos e justificativas para as respostas do grupo II. O teste inclui problemas sobre interseções de circunferências e eixos, reflexões em eixos de simetria, e propriedades de polinômios.
![Teste de Matemática A (n.º 2) – Versão 1 +2 10.º Ano
2
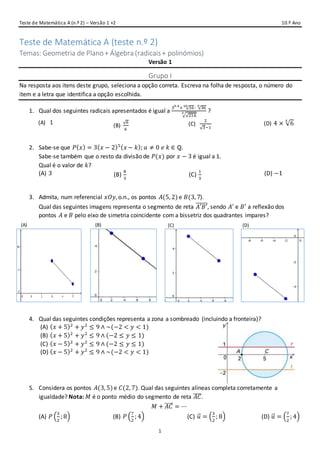
_Grupo II
Na resposta aos itens deste grupo, apresente todos os cálculos que tiver de efetuar e todas as justificações
necessárias.
Quando, para um resultado, não é pedida a aproximação, apresente sempre o valor exato.
1. Considere, num plano munido de um referencial cartesiano, um ponto 𝐴, a circunferência de centro
𝐴 definida pela equação ( 𝑥 − 1)2
+ 𝑦2
= 5, os pontos 𝐵 e 𝐶 de interseção da circunferência com o
eixo 𝑂𝑦 e o ponto 𝐷 de interseção da circunferência com o eixo 𝑂𝑥 e de abcissa negativa.
1.1. Determine as coordenadas dos pontos 𝐵, 𝐶 e 𝐷.
1.2. Determine por meio de uma condição a zona interior da circunferência de centro 𝐴 e exterior ao
triângulo [𝐵𝐶𝐷], incluindo as fronteiras.
1.3. Calcula a área do triângulo [𝐵𝐶𝐷].
1.4. Determina as coordenadas de:
1.4.1. 𝐵 + 𝐷𝐶⃗⃗⃗⃗⃗ 1.4.2. 𝐷𝐶⃗⃗⃗⃗⃗ − 𝐷𝐵⃗⃗⃗⃗⃗⃗
1.5. Determine as equações paramétricas da reta 𝑡, sabendo que esta é paralela à reta [𝐷𝐶] e que
passa no ponto 𝐴.
1.5.1. Qual é a inclinação da reta 𝑡, com 2 casas decimais.
1.6. Verifique se o vetor (√20− 2; −4) é colinear ao vetor diretor da reta 𝑡.
2. Efetua as operações indicadas e apresenta o resultado na forma de radical.
√ 𝑎−1 𝑏
1
2
3
× √𝑎2 𝑏−1
√ 𝑏−1
√ 𝑎33
(𝑎, 𝑏 ∈ ℝ+
)
3. Considera o polinómio 𝑃( 𝑥) = 2𝑥3
+ 3𝑥2
− 1.
a) Seja 𝑇(𝑥) o polinómio definido por [ 𝑃( 𝑥)]2
− 𝑃(𝑥). Qual é o grau do polinómio 𝑇(𝑥)?
b) Verifica que −1 é uma raiz de 𝑃(𝑥) e determina a sua multiplicidade.
c) Determina o conjunto solução da condição 𝑃( 𝑥) > −1.
d) Seja 𝐴( 𝑥) = 2 − 𝑥. Determina o conjunto solução da condição 𝐴( 𝑥) × 𝑃( 𝑥) < 0.
Grupo I – Escolha
Múltipla
Grupo II - Desenvolvimento Total
1 2 3 4 5 1.1 1.2 1.3 1.4.1 1.4.2 1.5 1.5.1 1.6 2 3
a
3
b
3
c
3
d
10 10 10 10 10 9 20 16 5 5 15 5 10 20 5 10 15 15 200](https://image.slidesharecdn.com/teste2-160721180016/85/Teste-2-Algebra-Geometria-de-Plano-10-ano-2-320.jpg)
![Teste de Matemática A (n.º 2) – Versão 1 +2 10.º Ano
2
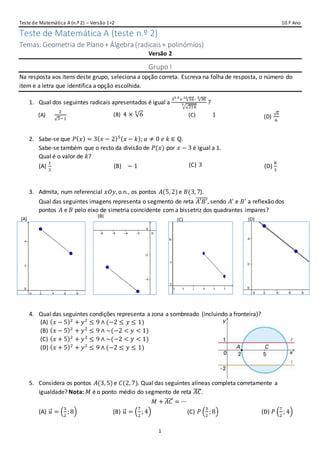
_Grupo II
Na resposta aos itens deste grupo, apresente todos os cálculos que tiver de efetuar e todas as justificações
necessárias.
Quando, para um resultado, não é pedida a aproximação, apresente sempre o valor exato.
1. Considere, num plano munido de um referencial cartesiano, um ponto 𝐴, a circunferência de centro
𝐴 definida pela equação ( 𝑥 − 1)2
+ 𝑦2
= 5, os pontos 𝐵 e 𝐶 de interseção da circunferência com o
eixo 𝑂𝑦 e o ponto 𝐷 de interseção da circunferência com o eixo 𝑂𝑥 e de abcissa negativa.
1.1. Determine as coordenadas dos pontos 𝐵, 𝐶 e 𝐷.
1.2. Determine por meio de uma condição a zona interior da circunferência de centro 𝐴 e exterior ao
triângulo [𝐵𝐶𝐷], incluindo as fronteiras.
1.3. Calcula a área do triângulo [𝐵𝐶𝐷].
1.4. Determina as coordenadas de:
1.4.1. 𝐵 + 𝐷𝐶⃗⃗⃗⃗⃗ 1.4.2. 𝐷𝐶⃗⃗⃗⃗⃗ − 𝐷𝐵⃗⃗⃗⃗⃗⃗
1.5. Determine as equações paramétricas da reta 𝑡, sabendo que esta é paralela à reta [𝐷𝐶] e que
passa no ponto 𝐴.
1.5.1. Qual é a inclinação da reta 𝑡, com 2 casas decimais.
1.6. Verifique se o vetor (√20− 2; −4) é colinear ao vetor diretor da reta 𝑡.
2. Efetua as operações indicadas e apresenta o resultado na forma de radical.
√ 𝑎−1 𝑏
1
2
3
× √𝑎2 𝑏−1
√ 𝑏−1
√ 𝑎33
(𝑎, 𝑏 ∈ ℝ+
)
3. Considera o polinómio 𝑃( 𝑥) = 2𝑥3
+ 3𝑥2
− 1.
a) Seja 𝑇(𝑥) o polinómio definido por [ 𝑃( 𝑥)]2
− 𝑃(𝑥). Qual é o grau do polinómio 𝑇(𝑥)?
b) Verifica que −1 é uma raiz de 𝑃(𝑥) e determina a sua multiplicidade.
c) Determina o conjunto solução da condição 𝑃( 𝑥) > −1.
d) Seja 𝐴( 𝑥) = 2 − 𝑥. Determina o conjunto solução da condição 𝐴( 𝑥) × 𝑃( 𝑥) < 0.
Grupo I – Escolha
Múltipla
Grupo II - Desenvolvimento Total
1 2 3 4 5 1.1 1.2 1.3 1.4.1 1.4.2 1.5 1.5.1 1.6 2 3
a
3
b
3
c
3
d
10 10 10 10 10 9 20 16 5 5 15 5 10 20 5 10 15 15 200](https://image.slidesharecdn.com/teste2-160721180016/85/Teste-2-Algebra-Geometria-de-Plano-10-ano-4-320.jpg)