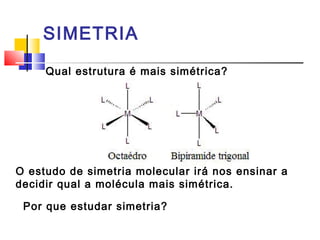
O documento discute os conceitos de simetria molecular, operações e elementos de simetria em moléculas, grupos pontuais e aplicações da simetria para determinar a polaridade e quiralidade de moléculas. Explica que a simetria molecular pode ser usada para entender propriedades físicas, orientar reações químicas e discutir estrutura eletrônica de moléculas.

1. SIMETRIA
MOLECULAR
Prof. SÁVIO

2. SIMETRIA
Correspondência em tamanho, forma ou arranjo, de
partes em lados opostos de um plano, seta ou
ponto, tendo cada parte em um lado a sua
contraparte, em ordem reversa, no outro lado.
Qual árvore é mais simétrica?

3. SIMETRIA
Qual estrutura é mais simétrica?
O estudo de simetria molecular irá nos ensinar a
decidir qual a molécula mais simétrica.
Por que estudar simetria?

4. SIMETRIA
• Determinar as propriedades físicas;
• Orientar como as reações podem ocorrer;
• Justificar os orbitais híbridos que são possíveis
em eterminadas moléculas;
• Construir diagramas de energia de orbitais
moleculares;
• Discutir estrutura eletrônica;
• Discutir vibrações moleculares;
• Atribuir transições em espectroscopia eletrônica.

5. OPERAÇÕES E
ELEMENTOS DE SIMETRIA
 Operação de simetria Þ Ação que
deixa a molécula aparentemente
inalterada.
 Ação Þ ROTAÇÃO através de um
ângulo, REFLEXÃO sobre um plano
ou INVERSÃO através de um ponto da
molécula.

6. OPERAÇÕES E
ELEMENTOS DE SIMETRIA
EXEMPLO DA ÁGUA
Uma molécula de água pode ser girada por qualquer
ângulo através da bissetriz do ângulo HOH, mas
somente um giro de 180° deixa-a aparentemente
inalterada. (C360/2 » C2)

7. OPERAÇÕES E
ELEMENTOS DE SIMETRIA
 Associada a cada operação de
simetria há um elemento de simetria.
Elemento de simetria
Um ponto, uma linha, ou um plano em relação ao
qual a operação de simetria é executada.

8. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Elemento de simetria: é a propriedade
geométrica que gera a operação.
 para uma rotação precisamos de um
eixo de rotação.
 Para uma reflexão precisamos de um
plano de simetria.
 Para uma inversão precisamos um
centro de inversão.

9. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
As operações e elementos de simetria mais importantes estão
resumidos na tabela

10. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 A operação identidade (E)ÞMantém a molécula inalterada.
Cada molécula tem no mínimo esta operação.
 Rotação por 360°/nÞUma n-ésima rotação é uma operação
de simetria se a molécula parece inalterada após a rotação
por 360°/n.
 O elemento de simetria correspondente à rotação é um n-ésimo
eixo de rotação C306°/n ou Cn.

11. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
Operação: ROTAÇÃO PRÓPRIA (Cn)
Elemento de simetria: EIXO DE
ROTAÇÃO PRÓPRIO (Cn onde
n =360o/ângulo de rotação)
Para água: C2

12. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Qual eixo tem a molécula de amônia?
 Quais as operações a partir desse eixo?
C3
+ C3
 Eixo de rotação C3
+
C3
-

13. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 A operação reflexão (s) em um dado plano de uma molécula é uma
operação de simetria se a molécula parece inalterada após esta
operação.
 O plano de reflexão(s) correspondente é o elemento de simetria.
 Na operação inversão (i) cada átomo é projetado numa linha reta por
um único ponto, a uma distância igual do outro lado do ponto, após
esta operação a molécula parece inalterada.
 O elemento correspondente é o centro de inversão (i).

14. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Quais os planos de reflexão na molécula H2O?

15. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Elementos de simetria na molécula de água.

16. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Quais os planos de reflexão na NH3?
 Há três planos de reflexão
verticais (sv) ao eixo
principal C3

17. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Quais os planos de reflexão na molécula do benzeno?
 Há um plano de reflexão horizontal (sh)
 Três planos de reflexão verticais (sv) ao
eixo de rotação principal C6
 Três planos de reflexão diedrais (sd) ao
eixo de rotação principal C6.

18. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Quais os eixos de rotação?
 Há um eixo de rotação C6
 Três eixos de rotação C2
perpendiculares ao C6

19. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 A operação de inversão e o centro de inversão i no
SF6
inversão

20. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Rotação imprópria (Sn) é uma operação composta.
Consiste numa rotação da molécula por um ângulo
de 2p/n ao redor de um eixo, seguido de uma
reflexão num plano perpendicular a este eixo.
 O elemento correspondente é o n-ésimo eixo de
rotação imprópria Sn

21. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Identifique as operações nos esquemas abaixo:
Operação de
inversão
Operação de
rotação C2

22. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Exemplo de um uma rotação imprópria (S4) na
molécula do CH4.

23. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Um eixo S1 equivale a uma plano de reflexão??
 Um eixo S1 equivale a C1 (giro de 360°) seguido de uma
reflexão perpendicular

24. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Um eixo S2 equivale a um centro de inversão i
 Um eixo S2 equivale a C2 (giro de 180°) seguido de uma
reflexão perpendicular

25. OPERAÇÕES E
ELEMENTOS DE
SIMETRIA
 Qual conformação de uma molécula CH3CH3 tem
um eixo S6?
Conformação não
eclipsada ou alternada

26. GRUPOS PONTUAIS
 GRUPOS DE PONTOS DAS MOLÉCULASÞOs
elementos de simetria da molécula determinam o grupo
pontual a que essa molécula pertence.
 Para atribuir o grupo de pontos de uma molécula, elabora-se
a lista dos elementos de simetria da molécula e
compara-se com a lista que define cada grupo de pontos.

27. GRUPOS PONTUAIS
 Tabela resumindo alguns grupos de pontos

28. GRUPOS PONTUAIS

29. GRUPOS PONTUAIS

30. lineare
s
cúbicos
IDENTIFICAÇÃO DE GRUPOS PONTUAIS
Cs
MOLÉCULA
S i ? S LINEAR N
N
D∞h C∞v
Dois ou mais
Cn, n>2?
S
S i ? N
C5 ?
N
S
Ih Oh Td
N Cn ? N
S
σ ?
N
S
i ?
N
S
C1
Ci
nC2 ┴ Cn ?
n maior possível
N
σ S h S ?
Dnh
N
nσd ?
S
N σh ?
Dnd Dn
Cnh
S
N
nσv ? S
Cnv
N
S2nN ?
Cn
S
S2n

31. Aplicações de Simetria
POLARIDADE DAS MOLÉCULAS
É uma molécula com um momento de dipolo elétrico permanente.
 Como a simetria pode nos ajudar?
 Uma molécula com um centro de inversão (i) é uma molécula
apolar. Por quê?
 A inversão implica que a molécula tem distribuição de carga igual
em todos os pontos opostos diametralmente ao centro i
 Um momento dipolar não pode ser encontrado perpendicular a um
plano de reflexão ou eixo de rotação
 Qualquer molécula que tenha um eixo C2 ┴ a um eixo Cn ou um
plana s h ┴ Cn não pode ser polar

32. Aplicações de Simetria
 A molécula rutenoceno [Ru(C5H5)] é
polar?
Grupo de
pontos D5h
Molécula apolar
D5h (E 2C5 2C5
2 5C2 2σ5 2S5 3 5σ

33. Moléculas Polares:
 1. Não apresentam centro de inversão.
 2. O momento de dipolo não pode estar perpendicular a
planos de reflexão.
 3. O momento de dipolo não pode estar perpendicular a
eixos de rotação.
 4. Moléculas que possuem eixos C2 ou σh perpendicular a
um eixo Cn possuem a resultante do momento de dipolo
igual a zero. Ou seja são apolares, apesar da existência
de dipolos. Grupos pontuais: D, T, O e I.

34. MOLÉCULAS QUIRAIS
 Uma molécula quiral não pode ser sobreposta na sua
imagem de reflexão.
 São opticamente ativas (quando observadas).
 Uma molécula quiral e sua imagem são chamados de
enantiômeros.
 Os pares enantioméricos giram o plano da luz
polarizada na mesma magnitude mas para lados
opostos.

35. MOLÉCULAS QUIRAIS
Os critérios da teoria de grupo para a quiralidade de uma molécula
são:
 Para ser quiral não pode ter Sn.
 Grupos que apresentam Sn são: Dnh, Dnd e os grupos Td e Oh.
 Cuidado com os eixos Sn disfarçados (s = S1; i=S2).
 Logo moléculas com um plano de reflexão não podem ser
quirais.
 Logo moléculas com centro de inversão não podem ser quirais.
 Moléculas Dn podem ser quirais.

36. MOLÉCULAS QUIRAIS
 A molécula CHClFBr é quiral? Com base na
teoria de grupo qual a simetria da molécula?
Br
Cl
F
H
Pertence ao
grupo C1 e não
Td

37. MOLÉCULAS QUIRAIS
 O íon [Cr(ox)]3- é quiral?
3 Ox = OCCO2-
22