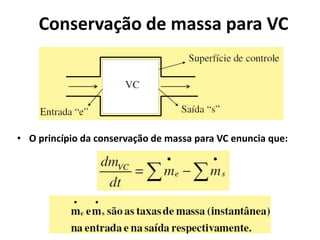
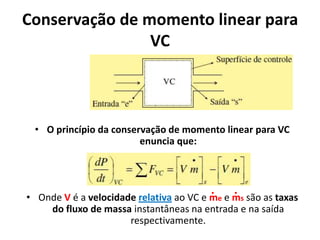
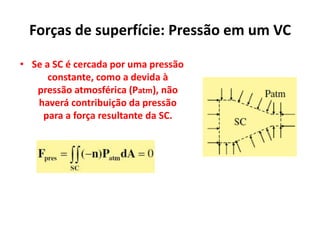
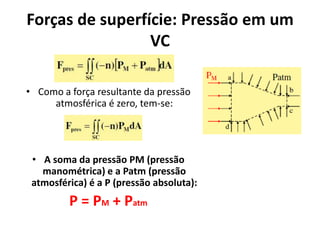
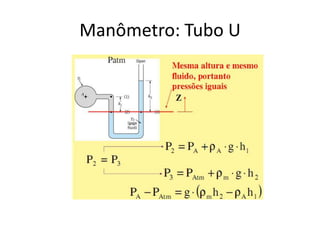
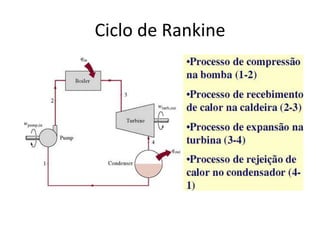
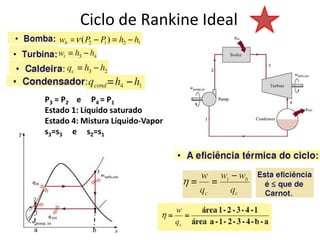
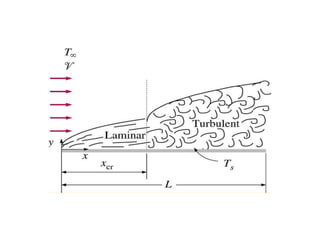
O documento discute princípios de conservação da massa, momento e energia para escoamentos em tubulações e dispositivos. Apresenta a equação de Bernoulli para escoamentos incompressíveis e o conceito de número de Reynolds para escoamentos laminar e turbulento. Explica os tipos de arrasto em objetos em movimento em um fluido.

1. Revisão P2Conservação da massa

2. Conservação da quantidade de movimento

3. Conservação da energia (escoamento de líquidos em RP)

4. Equação de Bernoulli ( + Manômetro: Tubo U)

5. Conservação da energia (dispositivos – turbina, bocal, bomba)

6. Variação de entropia em um VC

7. Ciclo de Rankine Ideal

8. Força de Arrasto e Coeficiente de de ArrastoConservação de massa para VCO princípio da conservação de massa para VC enuncia que:

9. Escoamento UnidimensionalConsiderando a velocidade de escoamento do ar (V) e a densidadedo ar( ), num escoamento unidimensional a taxa de massa ou vazão mássica (kg/s) será:Ou ainda:VAZÃO VOLUMÉTRICA: m3/s

10. Escoamento em regime permanenteAssim, num escoamento em regime permanente (a taxa de massa do VC se mantém constante) as taxas totais de entrada e saída de massa são iguais.

11. Conservação de momento linear paraVCO princípio da conservação de momento linear para VC enuncia que:Onde V é a velocidade relativaao VC e me e ms são as taxas do fluxo de massa instantâneas na entrada e na saída respectivamente.. .

12. Forças atuantes em um VCAs forças que atuam sobre o VC podem ser separadas em:Forças de campo: estão relacionadas com a massa de fluido no interior do VC.– Gravidade;Forças de superfície: são as que atuam na superfície do VC.– Pressão;–Tensão de cisalhamento (age tangencialmente à superfície do material)

13. Forças de superfície: Pressão em um VCSe a SC é cercada por uma pressão constante, como a devida à pressão atmosférica (Patm), não haverá contribuição da pressão para a força resultante da SC.

14. Forças de superfície: Pressão em um VCComo a força resultante da pressão atmosférica é zero, tem-se:A soma da pressão PM (pressão manométrica) e a Patm (pressão atmosférica) é a P (pressão absoluta): P = PM + Patm

15. Conservação de energia no VCO enunciado do princípio da conservação pode ser expresso desta forma:

16. Conservação de energia no VCEnquanto que no sistema (sem fluxo de massa) a taxa de energia armazenada é:No VC existe a contribuição da energia transferida através do fluxo de massa, sendo:onde Esup refere-se à transferência de energia devido ao esforço, atrito viscoso e pressão atuando na superfície de controle (SC) por conta do transporte de massa.

17. Conservação de energia no VCNo caso do VC possuir várias entradas e saídas, o balanço da taxa de energia é:Este balanço da taxa de energia estabelece a taxa na qual a energia cresce ou decresce em um VC.

18. Casos especiais: escoamento de líquidos em RPNão confundir com entalpia

19. Casos especiais: escoamento de líquidos em RPA carga manométrica total (HT), seja na entrada ou saída, é definida como a soma da carga manométrica de pressão (P/ρg), da carga manométrica de velocidade (V2/2g) e da carga manométrica potencial gravitacional (z) por unidade de vazão mássica.HT tem as dimensões de um comprimento (m ou ft).

20. Casos especiais: Equação de BernoulliEla é um caso particular da equação de conservação de energia, válida quando o escoamento for: – Incompressível (densidade constante) – Em regime permanente – Adiabático (sem transferência de calor) e reversível (sem dissipação viscosa ou invíscido) – Sem realização de trabalho

21. Casos especiais: Equação de BernoulliO termo ρ V2 /2 é a pressão dinâmica e existe apenas quando há escoamento.Fora da camada limite de escoamento, o escoamento se comporta como se fosse invíscido e a Eq. Bernoulli estabelece que a soma das pressões estática e dinâmica é constante ao longo da linha de corrente horizontal.Esta pressão constante é chamada de pressão total ou pressão de estagnação.

22. Manômetro: Tubo U

23. Princípio básico do tubo de PitotO escoamento livre é desacelerado de modo reversível até a estagnação.A energia total se conserva.Primeira solução que relaciona campo de velocidade com campo de pressão.

24. DispositivosEm Regime Permanente (RP)Bocais e DifusoresTurbinas Compressores e BombasTermo calculado em J. Para somar como valor da entalpia multiplicar por 10-3Termo na tabela em KJ

25. Variação de entropia em um VCS de um VC pode crescer de três formas: por adição de calor, por adição de massa ou pela presença de irreversibilidades.S de um VC pode diminuir de duas formas: por remoção de calor ou remoção de massa.

27. Ciclo de Rankine

28. Ciclo de Rankine IdealNeste ciclo ideal: – Todos os processos são reversíveis; – Não há queda de pressão nos trocadores de calor; – Não há irreversibilidades na turbina e na bomba.Será admitido regime permanente para todos os componentes.Cada componente será analisado em separado.A 1ª lei para VC:

29. Ciclo de Rankine IdealP3 = P2 e P4 = P1Estado 1: Líquido saturadoEstado 4: Mistura Líquido-Vapors3=s3 e s2=s1

30. Número de ReynoldsExiste um valor crítico de Re acima do qual o escoamento será turbulento e abaixo do qual será laminar.Este valor é conhecido como número de Reynolds de transição ou crítico.